The Wythoff construction

Until now we have been concentrating more on the geometric properties of the regular polyhedra and polychora and their regular compounds. However, as we will now see, a deeper understanding of these objects can be gained by studying how they can be built from their symmetries, in a process known as the Whythoff construction. This then makes it possible to summarise all information on a polytope in an extremely compact and elegant way, its Coxeter-Dynkin diagram. Apart from the improved understanding of polyhedra and polychora, this will be important for understanding regular polytopes in higher dimensions, where the geometric visualisation becomes difficult. This is meant only as a brief, non-technical introduction, for a rigorous treatment see Coxeter (1973).

The Wythoff construction in 2D

 The Wythoff construction is based on a very simple concept. In an object with, for instance, bilateral symmetry, the left and right sides are identical, but appear as if reflected in a flat mirror that goes through plane of symmetry of the object. Thus, in this case, we could start with the right side of the object and obtain the left side by reflecting it in that central mirror, generating the full symmetric object.

To a line associated with bilateral symmetry we add a second one perpendicular to it; in the following Figures these are in light blue. These lines act as mirrors, which define a specific kaleidoscope. These divide the plane in four regions, which are the fundamental domains of this particular 2-fold dihedral symmetry, which is a type of 2-D point symmetry (i.e., a symmetry around a single central point).



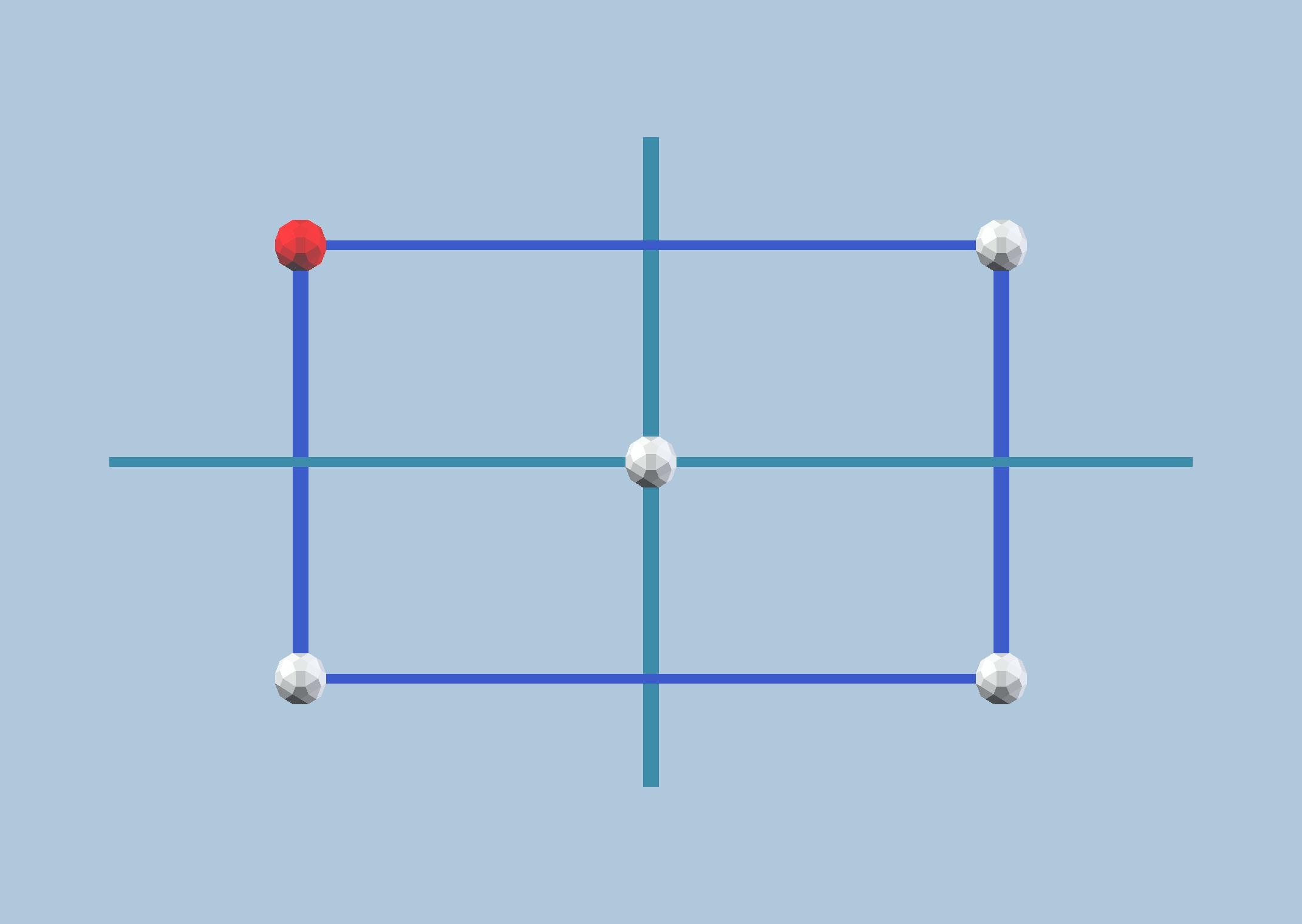
Fig. 9.1a: Two axes of bilateral symmetry define a 2-fold kaleidoscope. A point (in red) has a total of three other reflections (in white), connecting them we obtain a rectangle. Model made with vZome.



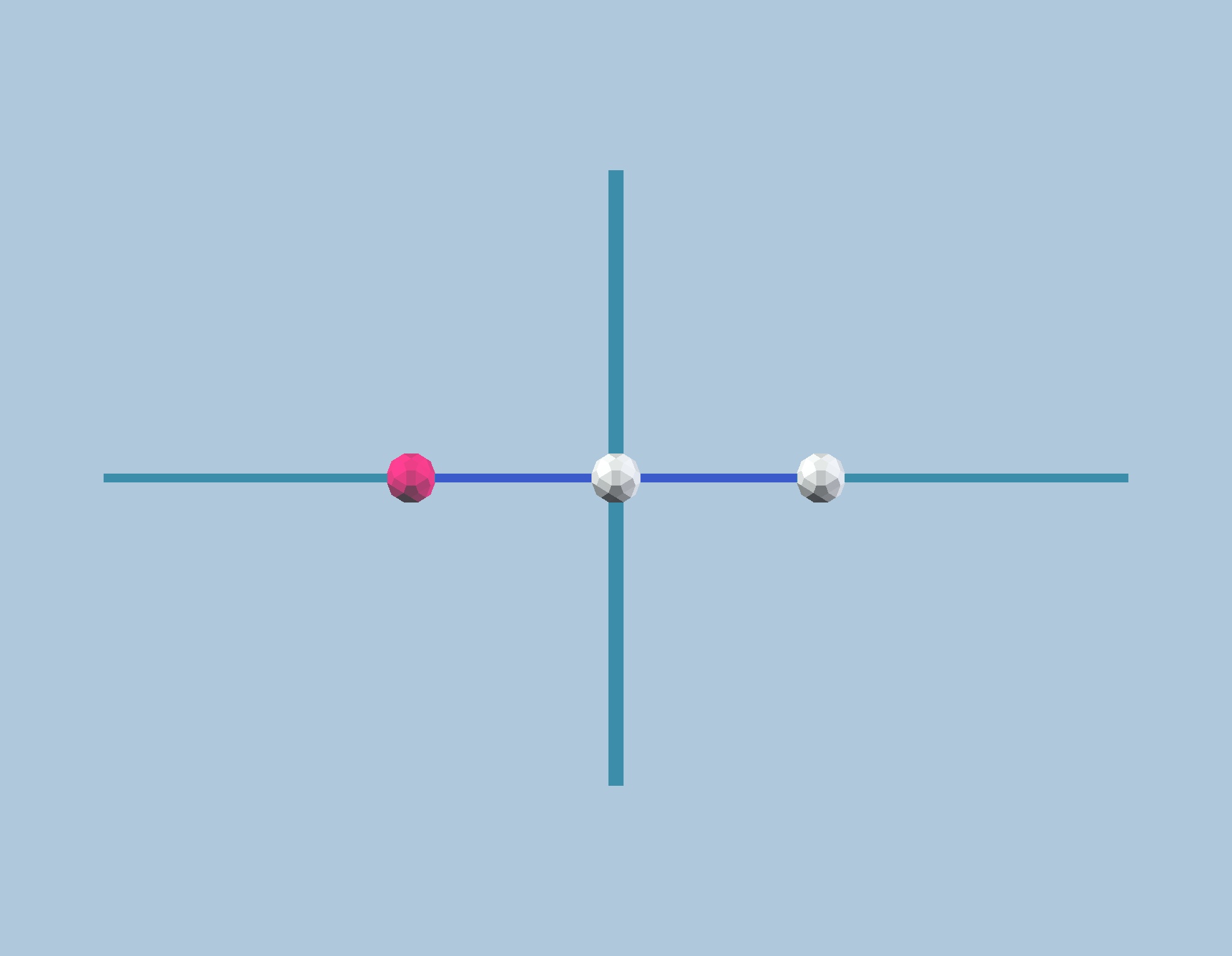
Fig. 9.1b: When a point is in one of the mirrors, it can only be reflected by the other mirror. In this case, this lead to the formation of a digon. Model made with vZome.



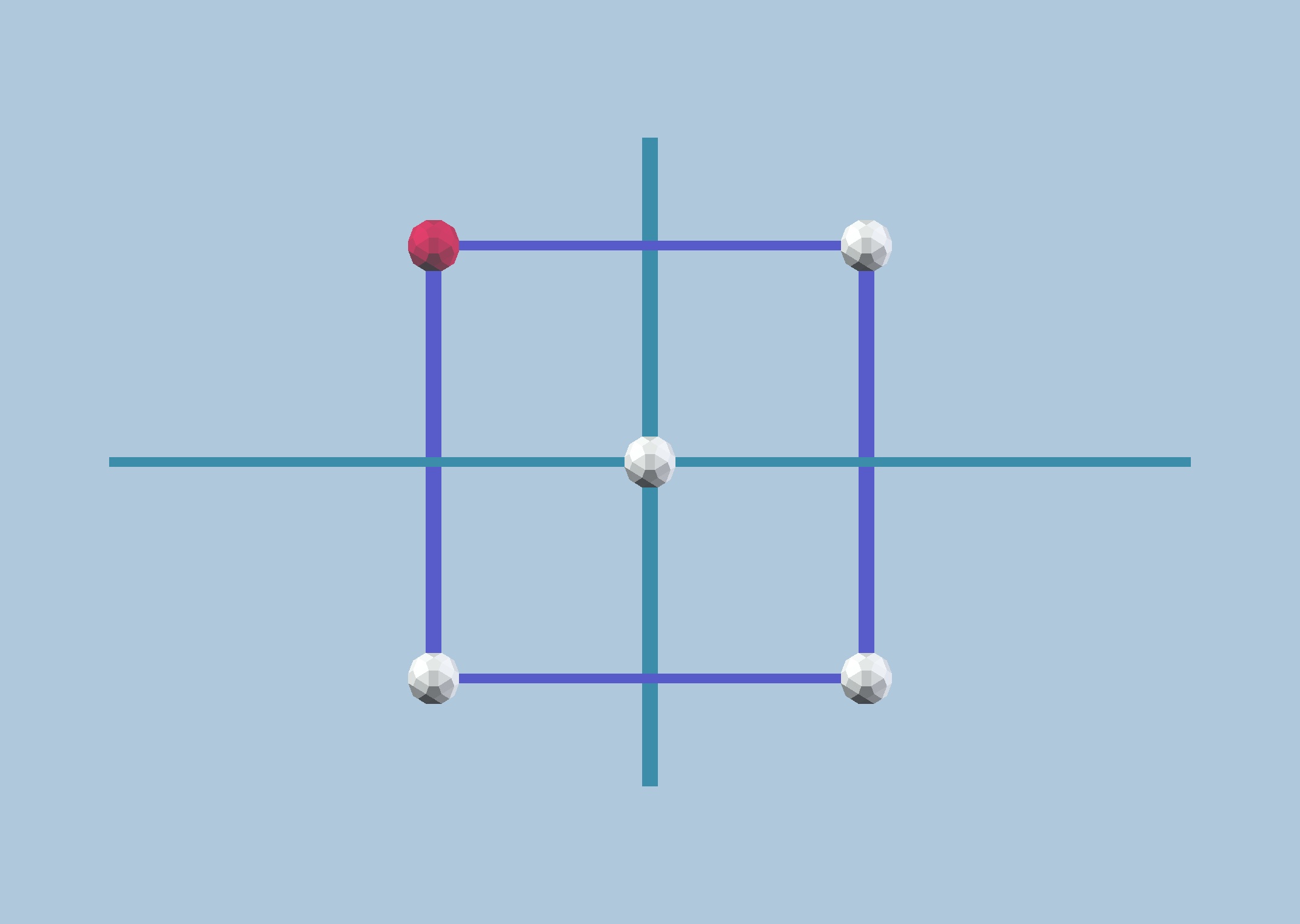
Fig. 9.1c: When a point is at the same distance from both mirrors, we obtain a Square. Model made with vZome.


Now, here comes the important feature. Kaleidoscopes reflect a single object in the fundamental domain into multiple copies. Our simple kaleidoscope in Fig. 9.1a does the same: starting with one of the vertices (in red), we can use the two mirrors to create the other three vertices. This is the basic idea of the Wythoff construction.

Connecting all vertices, we draw a rectangle. This figure has bilateral symmetry along two different axes. This has an implication: we can rotate it by 360 / 2 = 180-degrees and the figure will remain unchanged, something that does not necesarily happen for a figure with bilateral symmetry only. This is an illustration of an extremely important feature of these reflections, that they also define rotations : an even number of reflections is equivalent to a rotation, and odd number of reflections can always be expressed as a single reflection. This implies in general that just by rotating a figure we cannot flip it!

In Fig. 9.1b, we highlight an important fact: when a point is in a mirror, it coincides with its reflection by that mirror. The only noticeable reflection then is by a different mirror, i.e., only one mirror (the one where the vertice isn't) is active. In this case, the result is a 2-sided "polygon", a Digon.

In Fig. 9.1c, we reflect a point that is exactly in between the two mirrors. In this case, both mirrors are active. This generates a Square, which has 4-fold symmetry.

All these figures have an important feature, central symmetry.

The same thing can be done to any regular Polygon: in the case of a Triangle, we can choose a line going through its centre, one of its vertices and an opposing side that divides it in two equal parts. Flipping the whole figure around this line leaves it identical to itself (see Fig. 9.2a). This line is therefore an axis of bilateral symmetry.



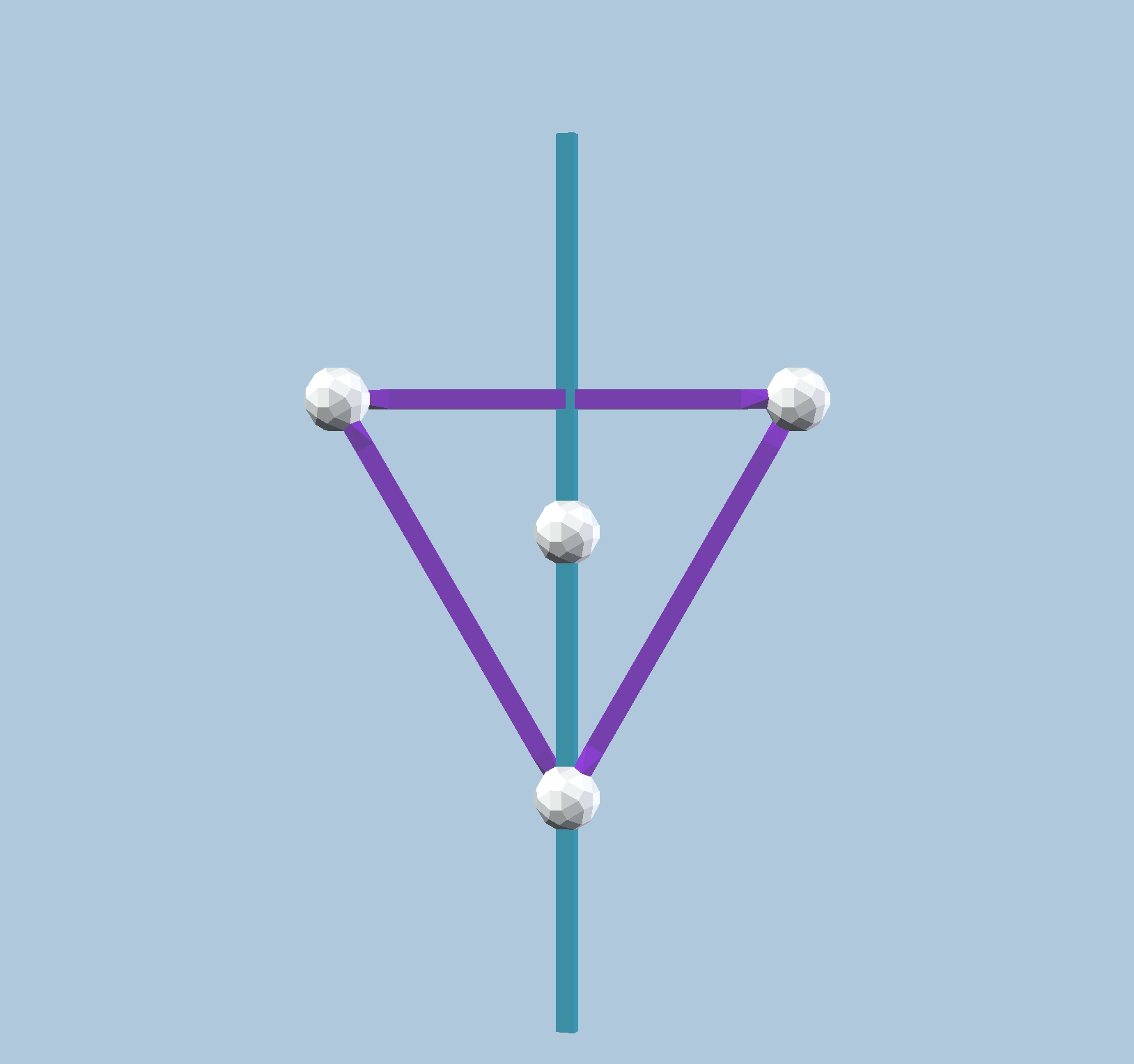
Fig. 9.2a: A regular triangle (in lavender color). The blue vertical axis defines one of the lines of bilateral symmetry. Model made with vZome.



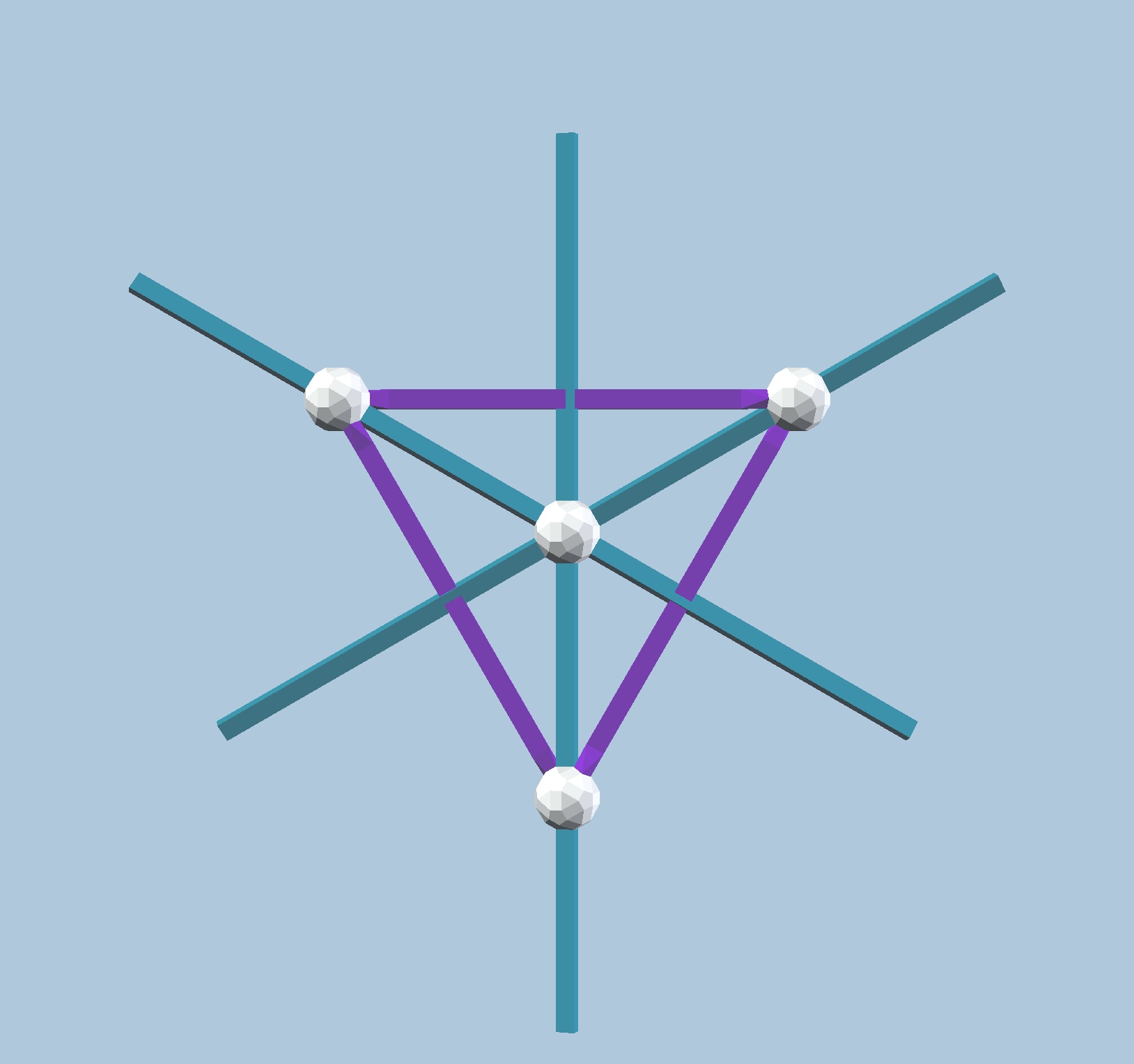
Fig. 9.2b: A Triangle has two more such axes of bilateral symmetry. These define the kaleidoscope of the 3-fold dihedral symmetry, where the plane is divided in six regions. Model made with vZome.


However, it should be clear that the Triangle has two other such lines, which cross at the centre of the triangle (Fig. 9.2b) They create six separate regions in the plane, which are defined by angles of 180 deg / 3 = 60 degrees, these are the fundamental regions of the 3-fold dihedral symmetry. Note that this symmetry has no central symmetry!

As before, different positions of initial points result in different figures. In Fig. 9.3a, moving the initial vertex from a point in an axis of bilateral symmetry to its neigbour, we create the dual Triangle, in red, i.e., we switched which mirror is active. For a point in the middle of the fundamental region, both mirrors are active, createing a regular polygon with 2n sides, in this case a Hexagon (Fig. 9.3b). If the initial point is not exactly at the same distance from the two mirrors, we create an irregular Hexagon, like the ditrigon in Fig. 2.3e. These represent different types of Wythoff construction acting on the same kaleidoscope.



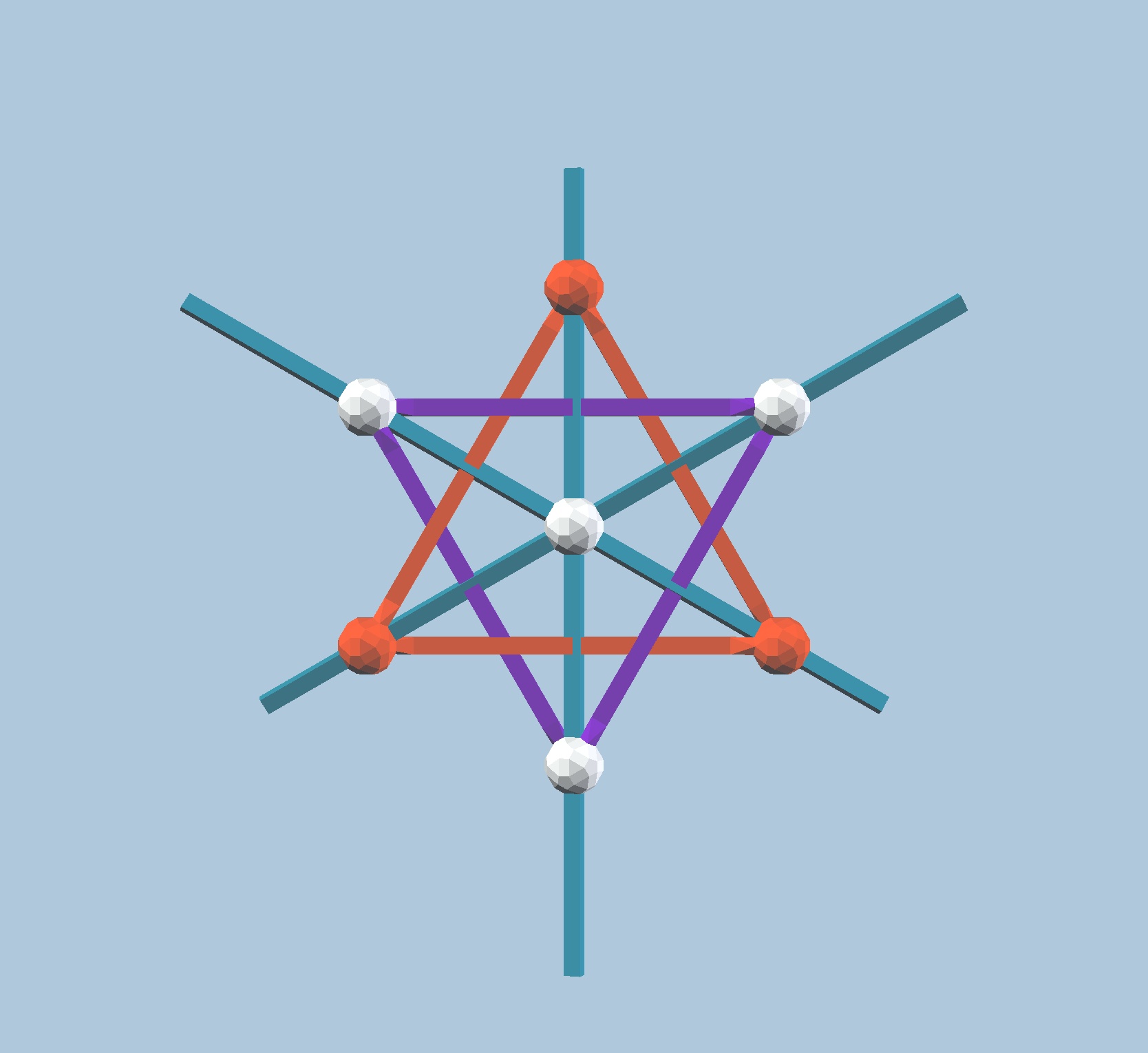
Fig. 9.3a: A point located in a neighbouring axis of bilateral symmetry creates a dual polygon, in red. Model made with vZome.



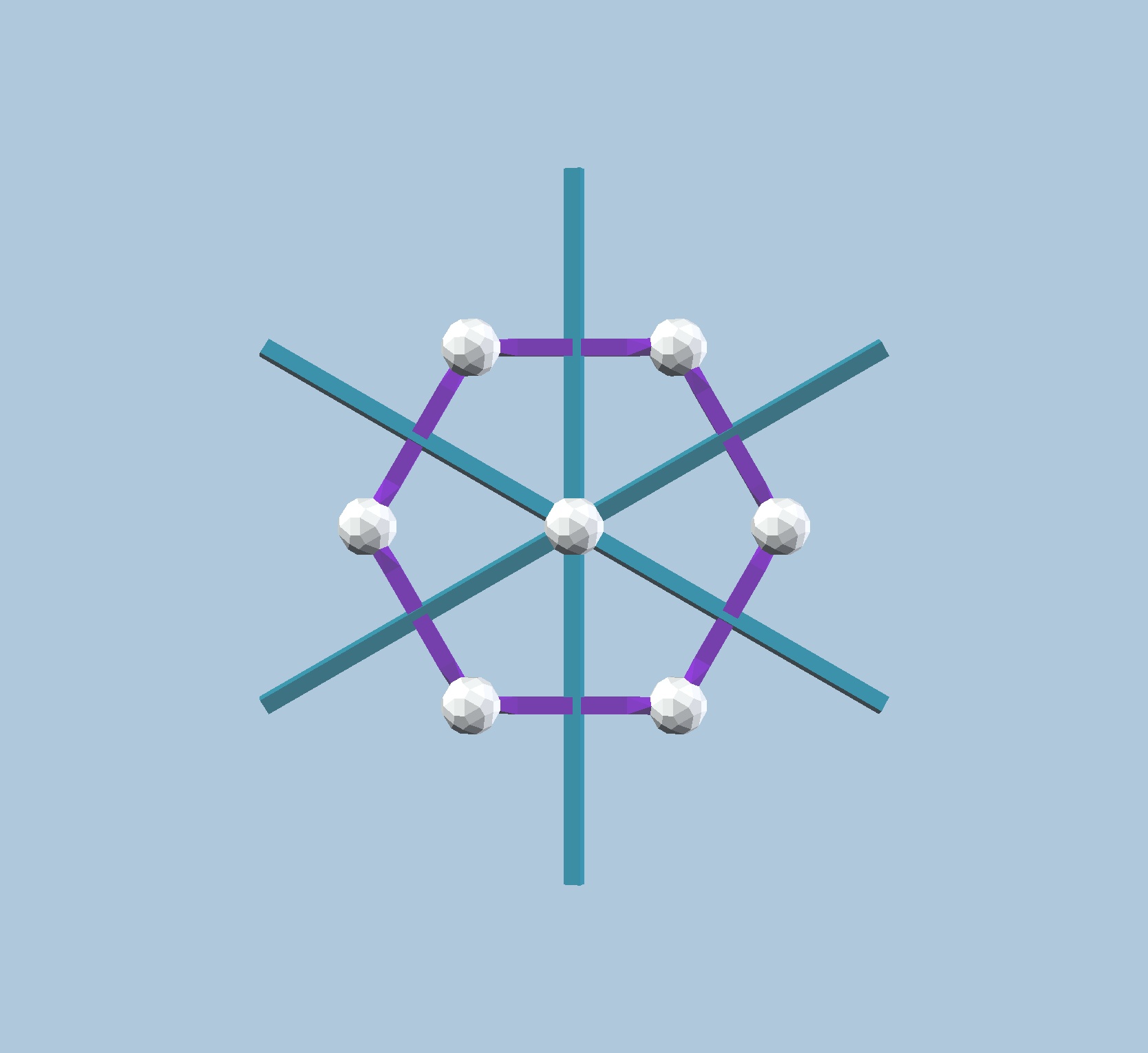
Fig. 9.3b: A point equidistant from the axes of bilateral symmetry produced a regular polygon with 2n sides.


The Square and Hexagon can, of course, also be obtained from 4-fold and 6-fold dihedral symmetry. The fact that they can also be derived from the 2-fold and 3-fold ditrigonal symmetries is a general feature of the Wythoff construction: in many cases, the same polytope can be obtained by different Wythoff constructions in different underlying kaleidoscopes.

The Wythoff construction in 3D

 We will now build the Kaleidoscopes associated with the regular polyhedra. The starting idea is the same: we start by looking for the planes of bilateral symmetry for the whole polyhedron, which go necessarily through the the centre of the whole figure. The full set of such planes then defines the 3-D polyhedral kaleidoscope, where they act as mirrors.

For a particular regular polyhedron A, it is clear that its planes of bilateral symmetry must go through its edges: each edge separates two identical faces, from each of these A looks identical. However, it is also true that the edges connect two identical vertices, from which A also looks identical. This implies that the lines perpendicular to the edges - the edges of the dual of A, here designated B, must also be coincident with planes of bilateral symmetry. Thus, all edges of the dual polytope compounds in Fig. 3.3a, b, and c are in the planes of bilateral symmetry of the dual pairs A/B.

However, looking at those figures, it is clear that the planes of bilateral symmetry define a further set of edges. To see them, we need to extend each edge "around" the polyhedron, making it an equatorial polygon. To do this, we add to the edges in models in Figs. 3.3a, b and c the edges used in making the Cube and other rhombic polyhedra. Doing this, we achieve a representation of the kaleidoscopes of the regular polyhedra, these are displayed in the next Figures.

Why specifically the rhombic polyhedra, and not the quasi-regular polyhedra, which are also isotoxal? The reason is that the rhombic solids are isohedral, thus the edges between faces must also be in the planes of bilateral symmetry.



Fig. 9.4a: The Tetrahedral kaleidoscope. The Tetrahedron is represented by the green HG2 struts, the other struts are there only to represent planes of bilateral symmetry.



Fig. 9.4b: The Octahedral kaleidoscope. In this model, we used HG2 struts for the edges of the Octahedron and half-blue 2 struts (in teal) for the edges of the Cube. The latter HB struts are very rare and unfortunately no longer made by the Zometool company. Using HB and HG struts allows the use of a single Y2 strut to represent the edges of the Rhombic dodecahedron.



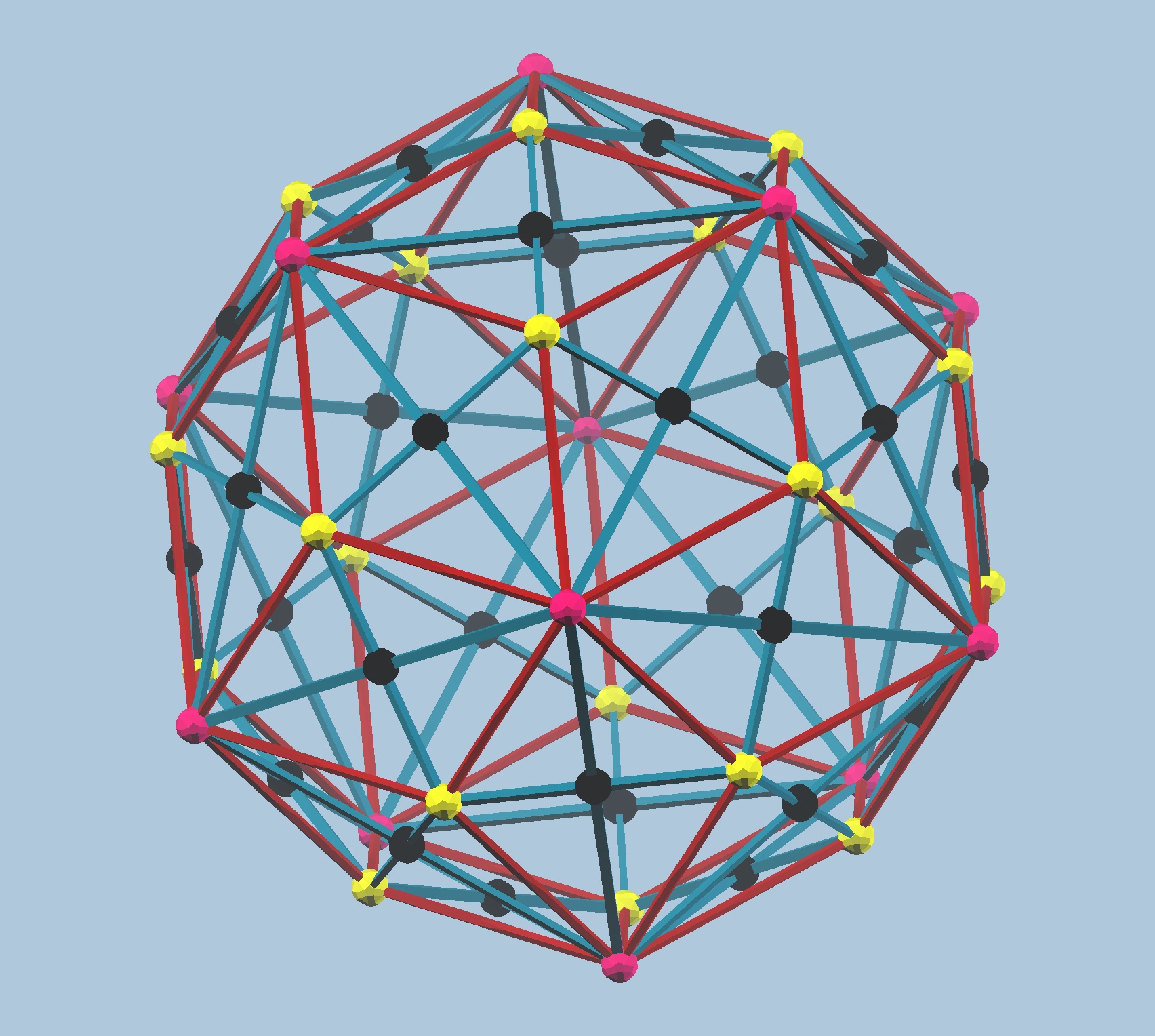
Fig. 9.4c: The icosahedral kaleidoscope. Note here how, using regular-sized B1 struts (for the edges of the Dodecahedron) and B2 struts (for the edges of the Icosahedron, in yellow) requires the use of two R1 struts to represent the edges of the Rombic triacontahedron (see Figs. 2.2d, 4.9).


We now discuss several details of these figures:

I colour-coded the vertices according to the axis of k-fold symmetry where they are located: red for the 5-fold symmetry (because those would connect to the centre with a R strut), blue for 4-fold symmetry (because those would connect to the centre with a B strut, although B struts have no 4-fold symmetry), Y for 3-fold symmetry (Y strut) and black for 2-fold symmetry, for consistency with the models in Figs. 3.3a, b and c.

Whenever possible, I used HG and half-blue (HB) struts. This made the construction more elegant, since I don't need to make all the edges of the Rhombic figures twice the length of a Y or R strut (see Fig. 4.9). The disadvantage is that HB struts are exceedingly hard to find, as they are no longer made by the Zometool company.

The requirement that both the edges of A and B appear in the figures does not complicate them: in the case of the Tetrahedral and Icosahedral symmetries, each equatorial polygon includes both the edges of A and B, as well as the edges of the rhombic polyhedra. For detailed images of the equatorial polygons, see Figs. 9.5a, b and c.

All planes of bilateral symmetry intersect at the centre, around which the 3-D point symmetry is defined. Outside that, they intersect along the axes of k-fold symmetry of the polyhedron. Around these axes, any elements - and the whole polyhedron - have a k-fold dihedral symmetry like that shown in Figs. 9.1a, b and c, 9.2a and b and Figs. 9.3a and b.

These planes divide a unit sphere around the central point into spherical triangles, known as Möbius triangles. They are the fundamental domains of the respective point symmetry. They correspond to the triangles of the models in Figs. 9.4a, b and c. Their angle at each vertex, which coincides with a k-fold symmetry axis, is 180 degrees/k, these numbers can be used to write them:

(2, 3, 3) triangles for the Tetrahedral symmetry, as we can see from Fig. 9.4a, 24 of these tesselate the sphere.

(2, 3, 4) triangles for the Octahedral symmetry, 48 tesselate the sphere (see Fig. 9.4b).

(2, 3, 5) triangles for the Icosahedral symmetry, 120 tesselate the sphere (see Fig. 9.4c).

In the case of all these triangles, the angles at the vertices add to more than 180 degrees. This is normal, these are spherical triangles. We should be aware that there are, of course, other symmetries other than those of the regular polyhedra. As an example, for a prism, we have instead: (p, 2, 2) triangles, where 2p triangles tesselate the sphere. There is no limit for p.

One interesting feature of the kaleidoscope in Fig. 9.4c is the distribution of the white connectors, which represent a slightly distorted version of the Rhombicosidodecahedron, an Archimedean solid. Instead of Square faces around the axes of 2-fold symmetry, this distorted version has Golden rectangles. Note how this represents the connectors themselves, and how the orientation of the connectors is identical to the orientation of the solid defined by the white connectors!

***

We've calculated the angles at the vertices of the Möbius triangles. We not calculate the lengths of their edges. These are the angles, measured from the centre, between the different axes of dihedral symmetry.

If we cut the models in Figs. 9.4a, b and c along their planes of bilateral symmetry, we can see their equatorial polyhedra. Their vertices are connected to the center by the axes of symmetry of the kaleidoscope, in these models we can see how they are arranged within these planes; they show where the plane intersects other planes of bilateral symmetry. The axes of symmetry are coloured like the balls they connect to, except for the axes of 2-fold symmetry: the balls are black, but the struts that connect to them (either by HG or HB) are coloured teal.



Fig. 9.5a: One of the six planes of bilateral symmetry of the Tetrahedral kaleidoscope.



Fig. 9.5b: Three planes of bilateral symmetry of the Octahedral kaleidoscope have 4-fold symmetry; they contain the equatorial Squares of the Octahedra.



Fig. 9.5c: The six other planes of bilateral symmetry of the Octahedral kaleidoscope are directly related to the six planes of bilateral symmetry of the Tetrahedral kaleidoscope. They are very different from the three planes of symmetry in Fig. 9.5b.



Fig. 9.5d: A plane of bilateral symmetry of the Icosahedral kaleidoscope. Note the overall 2-fold symmetry, which has 2 axes of bilateral symmetry. As in the case of the Tetrahedral kaleidoscope, all planes of bilateral symmetry are identical.


As discussed in the polyhedron page, the Tetrahedral kaleidoscope has four axes of 3-fold symmetry, and three of 2-fold symmetry, neither with central symmetry. It has six planes of bilateral symmetry, which go through opposite edges of the enveloping Cube. In Fig. 9.5a, note that the colours of the HG2 struts on top and below are different: the green one represents an edge of the Tetrahedron, the other one doesn't. This emphasises the fact that the Tetrahedral symmetry does not have central symmetry.

As discussed above, the Octahedral kaleidoscope has 3 axes of 4-fold symmetry, 4 axes of 3-fold symmetry and 6 axes of 2-fold symmetry. In Figs. 9.5b and c, we find an unusual characteristic of this kaleidoscope, that it was two different types of planes of bilateral symmetry. Three of these (Fig. 9.5b) have 4-fold symmetry; they contain the edges of the Octahedron, which form equatorial Squares. Their 4-fold symmetry implies that they are necessarily perpendicular to the 3 axes of 4-fold Octahedral symmetry. Six others have 2-fold symmetry, they contain the edges of the Cube and of the Rhombic dodecahedron. Their symmetry implies that they are necessarily perpendicular to the 6 axes of 2-fold Octahedral symmetry. Because they include opposite edges of a Cube, they have the same arrangement as the six planes of bilateral symmetry of the Tetrahedron.

As we've seen, the Icosahedral kaleidoscope has 6 axes of 5-fold symmetry, 10 axes of 3-fold symmetry and 15 axes of 2-fold symmetry. In Fig. 9.5d, we can see that its plane of bilateral symmetry has itself an overall 2-fold symmetry, with 2 blue axes of bilateral symmetry that are shared with the whole kaleidoscope. This symmetry implies these planes are necessarily perpendicular to the 15 axes of 2-fold Icosahedral symmetry; there are therefore 15 of these planes. We can check this by noting that each of the equatorial polygons includes 4 of the 60 edges of the Rhombic triacontahedron, and 2 of the 30 edges of the Icosahedron or Dodecahedron. From the symmetry of this figure, we can derive a fundamental fact, that unlike the Tetrahedral symmetry, the Octahedral does not "fit" within the Icosahedral symmetry. Indeed, in the Compound of five cubes, the arrangement of vertices and edges above the faces of the Cubes is not invariant under a 90-degree rotation; the same happens for the vertices of the Compound of five octahedra.

One of the advantages of these figures is that we can calculate very easily the angles between the axes of symmetry as seen from the central point. We now go in detail through these:
  1. In Fig. 9.5a, we see that the angle between the axes of 2-fold and 3-fold symmetry is the angle between the diagonal and the short side of the Yellow rectangle (Fig. 2.2b), this is arctan(√2) = 54.735 610 317 245... degrees. The angle between the two axes of 3-fold symmetry is 180 degrees minus twice the first angle, 70.528 779 365 509... degrees.
  2. In Fig. 9.5b, we see that the angle between the 2-fold and 4-fold symmetry axes of the Octahedral kaleidoscope is 45 degrees. In Fig. 9.5c, we see that the angle between the 2-fold and 3-fold axes of symmetry is the angle between the diagonal and the long side of the Yellow rectangle (Fig. 2.2b), this is arctan(1/√2) = 35.264 389 682 754... degrees. The angle between the 3-fold and 4-fold symmetry axes is the complementary, i.e., the angle between the diagonal and the short side of the Yellow rectangle (Fig. 2.2b), 90 − 35.264 389 682 754... = 54.735 610 317 245... degrees, which we have met already in the Tetrahedral kaleidoscope.
  3. In Fig. 9.5d, we see that the angle between the axes of 2-fold and 3-fold symmetry is the angle between the diagonal and the long side of the Long yellow rectangle (Fig. 2.2e), this is arctan(1/φ2) = 20.905 157 447 889 degrees. The angle between the axes of 2-fold and 5-fold symmetry is the angle between the diagonal to the the long side of the Golden rectangle (Fig. 2.2d), this is arctan(1/φ) = 31.717 474 411 461... degrees. Finally, we see that the angle between the axes of 3-fold and 5-fold symmetry is 90 degrees minus the other two, 37.377 368 140 649... degrees.
These are thus the lengths of the edges of the spherical Möbius triangles. They add to 180, 135 and 90 degrees in the cases of the Tetrahedral, Octahedral and Icosahedral kaleidoscopes. They are all the information we need to build these kaleidoscopes. Detailed instructions on how to do build paper models are provided by Wenninger (1974). Detailed instructions on how to build actual working kaleidsocopes, with mirrors, are provided by Coxeter (1991), chapter 3.

***

The kaleidoscopes associated with the symmetries of the regular polyhedra are now completely defined. We can refer to its planes of bilateral symmetry as mirrors, since they reflect each half of the polyhedron into another half. We now illustrate the Wythoff construction using these Zometool models of their kaleidoscopes: From this, it is clear that the regular polyhedra and their rectifications share the same type of Wythoff construction: Their vertices are reflections of one of the three vertices of the Möbius triangle (i.e., of points lying on the symmetry axes of the kaleidoscope) by a single mirror, the one opposite to that vertex. Thus, in each case, only one mirror is active. The fact that a triangle has only three vertices means that for each pair of dual regular polyhedra (i.e., for each type of symmetry) there is only one rectified form.

The main difference between two dual regular polyhedra and their rectification is the way the edges are reflected. As we've seen in the derivation of the kaleidoscopes, the edges of two dual regular polyhedra are necessarily in the planes of bilateral symmetry: they coincide, respectively, with the two sides of the Möbius triangle that meet at a right angle (at the black balls in Figs. 9.4a, b and c). Each such edge is shared by a total of 4 such triangles, their number is therefore the number of Möbius triangles in each symmetry / 4.

However, for the rectifications, this is not the case, as shown in Fig. 9.6.



Fig. 9.6: Icosahedral kaleidoscope, as in Fig. 9.4c, now with one edge of the Icosidodecahedron (B2 strut in teal).


In this figure we start with the model of the Icosahedral kaleidoscope in Fig. 9.4c. As we've seen above, the long side of the Möbius triangle is that of a Rhombic polyhedron, in this case of a Rhombic triacontahedron. Here one of these sides (highlighted by the black line) is reflecting one of the points of 2-fold symmetry, A, into a second one, A'. Uniting A and A' is one of the edges of the Icosidodecahedron (represented by a B2 strut in teal), which is therefore (as we've seen in the polyhedron page) perpendicular to those of the Rhombic triacontahedron. This means that the edge of the Icosidodecahedron does not coincide with any edge of the Möbius triangle and is therefore within that triangle. In the Figure, we also see how the edge of the Icosidodecahedron is shared equally by two Möbius triangles, as are the edges of the Rhombic triacontahedron. This implies that their number is the number of Möbius triangles in each symmetry / 2; i.e., twice the number of edges of the regular polyhedra.

We also see here that the way the edges of the rectifications are reflected by the two perpendicular mirrors implies that there are four of them meeting at each of those black balls. Therefore, they necessarily have a rectangular vertex figure, which as we've seen in Fig. 9.1a, is a general product of the 2-fold symmetry around the black balls. As we've seen already in the polyhedron page, the central symmetry of these vertex figures implies that these rectifications have equatorial Polygons.

One interesting fact, which we have already mentioned, is that the rectification of the Tetrahedron is itself also regular, an Octahedron; its vertices are the black balls in Fig. 9.4a, these are reflected by a single mirror, which in that figure is represented by the edges of the Cube. Its edges are therefore perpendicular to those of the Cube, they are the edges of the Octahedron. This highlights that, as for even-sided polygons (like the Hexagon in Fig. 9.3b), some polyhedra can also have multiple Wythoff constructions. This particular case of a multiple Wythoff construction will be of importance for what follows.

There are other possible types of Wythoff construction for polyhedra, which are associated with reflecting points located in the edges and inside the Möbius triangles. The result of such constructions are the Archimedean solids.

***

A final question: can the regular star polyhedra be derived using the Wythoff construction? The answer is yes, only that the Wythoff construction reflects vertices of Schwarz triangles, which have surfaces that are multiples (by a factor of d) of those of the Möbius triangles. These cover the sphere d times as a multi-connected Riemann surface. The number d is known as the density of the resulting polytopes. The only two Schwarz triangles that yield regular polyhedra (the Kepler-Poinsot polyhedra) are:

(2, 5/2, 5) - these have d = 3; they generate the Stellated dodecahedron and the Great dodecahedron.

(2, 5/2, 3) - these have d = 7; they generate the Great icosahedron and the Great stellated dodecahedron.

Because they have a right angle (the "2" at the start), they also generate the rectifications of these polyhedra, respectively the Dodecadodecahedron and the Great icosidodecahedron, which have similar properties to the rectifications mentioned above. There are many other Schwarz triangles, which generate all but one of the 75 non-prismatic uniform star polyhedra, the "Star archimedeans".

However, there are cases where multiples of the smaller Möbius triangles fit into larger Möbius triangles. This is the origin of the regular compounds: as the Wythoff construction starts reflecting the vertices of these triangles, it will only generate the vertices of the regular polyhedra with the symmetry associated with those triangles. Two Möbius triangles of the Octahedral group fit inside a Möbius triangle of the Tetrahedral group (their numbers are 48 and 24 respectively) this gives rise, via the Wythoff construction, to the Stella Octangula, which has d = 2. Five Möbius triangles of the Icosahedral group fit inside a Möbius triangle of the Tetrahedral group (their numbers are 120 and 24 respectively); this gives rise to the regular compounds with Icosahedral symmetry, which have d = 5 or 10.

***

Just like we can apply the concept of the Wythoff construction to polyhedra, we can also apply it to the regular tilings of 2-D Euclidean space, which are no longer point symmetry groups, but flat analogs of the polyhedral surface. Doing this, we obtain all the Archimedean tilings of 2-D Euclidean space, with the exception of the elongated triangular tiling, which is non-Wythoffian. These tilings are of practical interest for fields like architecture, design and engineering.

The Wythoff construction in 4D

 The Wythoff construction works in analogously in any dimensional space. We will now discuss in particular how things work in 4 dimensions.

To build the kaleidoscope, we must first have a central point, from where the 4-D point symmetry is defined. Intersecting at this point are "hyperplanes" of bilateral symmetry. These 3-D "planes" intersect a 3-sphere centred on that point along particular 2-D surfaces. These divide the 3-sphere into Goursat tetrahedra, the fundamental domains of these 4-D point symmetries.

The vertices of these tetrahedra correspond to the intersections of the 3-Sphere with axes of polyhedral symmetry - as we've seen, projecting the polychoron along these axes we obtain projections with the respective symmetry. The edges of these tetrahedra correspond to the axes of k-fold dihedral symmetry we've seen for polyhedra; if an edge of the polychoron is coincident with one of those, its edge figure is a k-sided polygon, if a face is perpendicular to them, it is a k-sided polygon as well. As mentioned just above, the faces of these tetrahedra are associated with bilateral symmetry. This means that faces of a regular polychoron must be in their planes: since two identical cells connect at each face, the faces must be coplanar with planes of bilateral symmetry. The edges of a polychoron must be perpendicular to them, because these link two identical vertices.

For two dual polychora A and B, two of the vertices of polyhedral symmetry of the Goursat tetrahedron correspond to the the centres of cells and vertex figures of A, which by duality correspond to the vertex figures and cells of B, with the same symmetries. What about the other two vertices? These can be found easily from the fact mentioned above that each edge and each face of a regular polychoron are associated, at the same time, with bilateral and dihedral symmetry. Thus, their central points correspond to axes of a polyhedral symmetry of the polychoron that combines dihedral and bilateral symmetry: the prismatic symmetry.

The vertices of two dual regular polychora A and B are built by reflecting vertices in the first two types of vertices of the Goursat tetrahedron. As for the polyhedra, the rectifications of regular polychora also share the same type of Wythoff construction: their vertices are reflections of vertices of the Goursat tetrahedron, but those associated with prismatic symmetries. Since the fundamental region is a Tetrahedron (with 4 vertices), for two regular polychora there are in general two rectifications. Like the rectifications of regular polyhedra, all their edges are identical.

***

We have already seen rectifications of regular polychora: the rectified 5-cell (Fig. 5.3), rectified 16-cell (which is also the 24-cell, see Figs. 5.5a and b) and rectified 24-cell (Fig. 5.6). However, because of the self-duality of the 5-cell and 24-cell, they have only one rectification; therefore they not provide a good illustration of the two different rectifications we generally expect from reflecting points on the prismatic vertices of the Goursat tetrahedron. Furthermore, the rectification of the 16-cell is unusual in being regular, the 24-cell.

In the next two Figures, we show the rectifications of the 120-cell and 600-cell, which share their Hexacosichoric symmetry but are clearly different. In both of them, we can see clearly how their vertices (which appear in the middles of the edges of the polychora they rectify) are associated with prismatic symmetries: their vertex figures are a Triangular prism in the case of the 1200 vertices of the Rectified 120-cell in Fig. 9.7 and a Pentagonal prism in the case of the 720 vertices of the Rectified 600-cell in Fig. 9.8. These vertices are reflections of the points associated with the Triangular and Pentagonal prismatic symmetries of the Goursat tetrahedra, they mark the position and number such points in the Hexacosichoric kaleidoscope.



Fig. 9.7: The icosidodecahedral cell-first projection of the Rectified 120-cell.

How to build: Study the perspective-flattened Dodecahedra in the model of the 120-cell. Make models of Icosidodecahedra with similar flattening. Then have a look at the Eusebeia page on the Rectified 120 cell.
Picture taken by Jason Wu.


In the Icosahedral projection of the rectified 120-cell, the Dodecahedra of the 120-cell are replaced by their rectifications, Icosidodecahedra. Under each of the 600 vertices of the 120-cell, a Tetrahedron (the vertex figure of the 120-cell) appeared. Each edge is shared by a Tetrahedron and two Icosidodecahedra. This Icosahedral projection is necessarily centred on an Icosidodecahedral cell. Each edge is shared by two Icosidodecahedra and one Tetrahedron. Three Icosidodecahedra and two tetrahedra meet at each vertex.

In the page on the regular convex polychora, we have seen two semi-regular convex polychora (which, apart from being Uniform, have only regular cells, in these cases of two distinct types): the Rectified 5-cell and the Snub 24-cell. There is a third and last semi-regular convex polychoron, the Rectified 600-cell. Like the Rectified 5-cell, this results from rectifying a regular convex polychoron with Tetrahedral cells: the 600 Tetrahedra of the 600-cell are replaced by their regular rectifications, Octahedra. Under each of the 120 vertices of the 600-cell new Icosahedra (the vertex polyhedron of the 600-cell) appeared; all their projections were already visible in the model of the 600-cell in Fig. 5.10. Each edge is shared by one Icosahedron and two Octahedra. Three Icosahedra and five Octahedra meet at each vertex.



Fig. 9.8: The Icosahedral projection of the Rectified 600-cell. This projection is the rectification of the Icosahedral projection of the 600-cell.

How to build: After studying the perspective-flattened Icosahedra in the model of the 600-cell, have a look at the Eusebeia page on the Rectified 600 cell. Also recommended is David Richter's page on the Rectified 600-cell.


Also, as for the other semi-regular polychora, all faces are Triangular. Since all faces are Triangular, the prismatic vertex figures are necessarily edge sections located under each vertex, as in the case of the Rectified 5-cell and Rectified 16-cell (the 24-cell).

If you pay close attention to the model, you will be able to see several Archimedean solids in blue, starting with Icosidodecahedra - the rectifications of the Icosahedral sections of the 600-cell. These polyhedra are edge sections of the Rectified 600-cell. Because they have Icosahedral symmetry, they appear ``under'' the Icosahedral cells in 4-D space, around the central cells in this projection. Studying the model further, you will be able to see many flattened versions of those. All these sections are the cells of 14 non-convex polychora, all of them edge facetings of the Rectified 600-cell and therefore represented by the same model. One of them is the Rectified icosahedral 120-cell, which has Great dodecahedra and Icosidodecahedra as cells (for more about the Icosahedral 120-cell, see the page on regular star polychora). These 14 edge-facetings are a sub-group of the 60 facetings of the Rectified 600-cell that are uniform, non-convex polychora.

In these models, we can see a general feature of these rectifications: the prismatic symmetries around their vertices have no central symmetry. This means that there are no equatorial polyhedra associated with them, which is unlike what we find for most of the regular polychora. The situation is almost the reverse of what we find among regular polyhedra, where only one of the nine regular polyhedra (the Octahedron) has equatorial polygons, but all their rectifications have, by virture of their rectangular vertex figures, equatorial polygons. On the other hand, the Icosidodecahedral cells of the Rectified 120-cell and all cells of the Rectified 600-cell have central symmetry. This means that we can see equatorial cell rings. Some of these are visible along the 5-fold symmetry axes of the Rectified 120-cell (we see one of these at the centre of Fig. 9.7), because the Icosidodecahedra connect to each other at common Pentagonal faces. For the Rectified 600-cell, equatorial cell rings are visible along the 3-fold symmetry axes, and they include alternate Octahedra and Icosahedra, which connect with each other at their common Triangular faces.

There are other possible types of Wythoff construction for convex polychora, which are associated with reflecting points located in the edges, faces and inside the Goursat tetrahedra.



Fig. 9.9a: The Truncated 600-cell, here seen along one of its 5-fold symmetry axes.



Fig. 9.9b: The same model as above, seen here from a 3-fold symmetry axis.

How to Build: See the Eusebeia page on the Truncated 600-cell


A reflection of a point in an edge of the Goursat tetrahedron is a truncation. In Figs. 9.9a, b, we see the Icosahedral projection of the Truncated 600-cell. It is similar to the Rectified 600-cell above, and it also has 120 Icosahedral cells. However, instead of 600 Octahedral cells, it has 600 Truncated tetrahedral cells. In Fig. 9.9b, we see the model along a cell ring that lies along one of the 3-fold axes of the model. Along this axis, two Truncated tetrahedra connect to each other via common Hexagonal faces, and to Icosahedra via common Triangular faces.

The rectifications discussed above, the Snub 24-cell and the Truncated 600-cell are examples of Archimedean polychora; these are discussed in more detail here.

***

Just like we can apply the concept of the Wythoff construction to polychoral kaleidoscopes, we can also apply it to Goursat tetrahedra that fill 3-D Euclidean space. In these cases, we are no longer dealing with the type of kaleidoscope associated with finite point-symmetry groups. Doing this, we obtain most of the uniform honeycombs, the flat analogues of uniform polychoral surfaces, one of these, the Cubic honeycomb, is regular. However, some such uniform tilings are non-Wythoffian. These honeycombs are of practical interest for fields like architecture, design, engineering and crystallography.

Coxeter-Dynkin diagrams

 To proceed, we will now investigate in some detail the concept of a Coxeter-Dynkin diagram (henceforth CD diagrams). These are graphs that describe the fundamental regions of the kaleidoscopes we have seen above and the polytopes built from them in an extremely compact and elegant way.

For dihedral symmetries, like the 2-fold (Figs. 9.1a, b and c) and 3-fold symmetry (Figs. 9.2a and b and 9.3a and b), the graph consists of two dots with line between them. The two dots represent the two mirrors that define the border of the fundamental region. The line indicates the dihedral symmetry of the kaleidoscope, i.e., the angle between the mirrors.

Below, we represent these graphs (how else?) with the Zometool: the dots are connectors, the lines are struts. The graphs have the following rules: for a 2-fold symmetry, the line is invisible, i.e., there is no strut! The 3-fold symmetry is indicated by an unmarked line (in the Zometool version, a yellow strut). For 4 and 5-fold symmetries, the lines have a number above them indicating the dihedral symmetry; in the Zometool version we will indicate these with blue or red struts, as these represented these symmetries in the corresponding vertices in the models of the kaleidoscopes in Figs. 9.4a, b and c and 9.5a, b, c and d.



Fig. 9.10: CD graphs for dihedral kaleidoscopes (left), and for the polygons built with them (on the right).


The graphs described above represent only the kaleidoscope. To represent a polytope, the nodes are ringed, indicating which mirrors of the fundamental region are active during the Wythoff construction. In the Zometool version, we represent ringing by turning a connector black. Ringing a single node indicates that only one mirror is active, this means that the point being reflected is located in the other mirror (Figs. 9.1b, 9.2b). Doing this, we obtain a Polygon with the same number of sides as the symmetry. Ringing the other node means that the other mirror is the one that is active, in this case we obtain the dual Polygon (red Triangle in Fig. 9.3a). Ringing both nodes indicates that both mirrors are active, i.e., the point is in the middle of the fundamental region: we then obtain a polygon with twice the number of sides (the Square in Fig. 9.1c and the Hexagon in Fig. 9.3b). Note that the Square is also obtained by ringing a single node of the graph associated with the 4-fold dihedral symmetry, this is a reflection of the aforementioned fact that the same polytope can result from different Wythoff constructions acting on different kaleidoscopes.

***

For 3-D symmetries, the CD graphs have three nodes and three lines connecting them. The lines correspond to the vertices of the Möbius triangles, and list the dihedral symmetries associated with each vertex, following the same rules as in Fig. 9.10. One of the consequences (at least for the polyhedral kaleidoscopes we studied above) is that one of the lines is invisible, the line corresponding to 2-fold symmetry. This is the reason why these graphs are represented by lines, instead of having the triangular shapes they depict. Not all kaleidoscopes have a single invisible line: the prismatic symmetries include two empty lines, some other symmetries have no invisible lines.



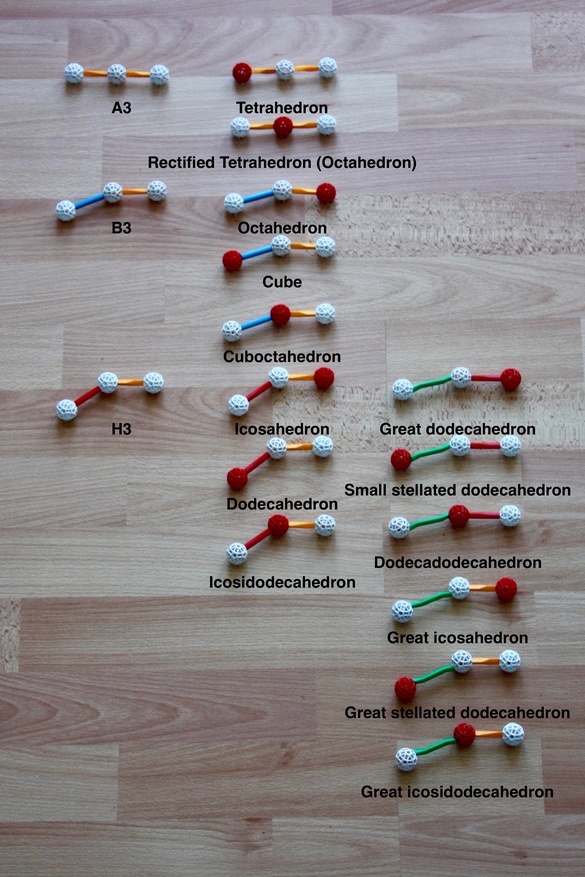
Fig. 9.11: CD graphs for polyhedral kaleidoscopes (left), and for the polyhedra built with them (right).


As above, the nodes represent the edges of the Möbius triangles, the mirrors of the kaleidoscope. Ringing a node indicates its mirror is active during the Wythoff construction. Again, ringing a single node means that only one mirror is active, i.e., the point being reflected is at the intersection of the other two mirrors, i.e., in one of the vertices of the Möbius triangle.

Ringing one end node of the graph represents, in the symmetries in Fig. 9.11, the construction of a regular polyhedron. Ringing the node at the opposite end of the graph produces the dual regular polyhedron. If the CD graph is symmetric (which it is for the Tetrahedral symmetry), then the regular polyhedra obtained from ringing either end are identical (Tetrahedra), this means that the tetrahedron is self-dual. Ringing the middle node produces the rectification of the regular polyhedra. Importantly, note the two graphs for the Octahedron, which can be obtained by ringing an end node in the Octahedral symmetry, and the middle node in the Tetrahedral symmetry. This represents two different Wythoff constructions of this polyhedron.

These graphs are very instructive. Cutting a note at the end opposite to the one being ringed we see the faces of the polyhedron, in the example at the bottom we do this for the Dodecahedron, revealing a Pentagon. Cutting the ringed node, and ringing the one closer to it, we see the vertex figure, when we do this to the Dodecahedron, we see a Triangle. For the rectified polyhedron, we see that both polygons are faces, as both touch the node being ringed.

***

For 4-D symmetries, the CD graphs extend those in Fig. 9.11, they now represent the four polyhedral symmetries associated with the Goursat tetrahedron.



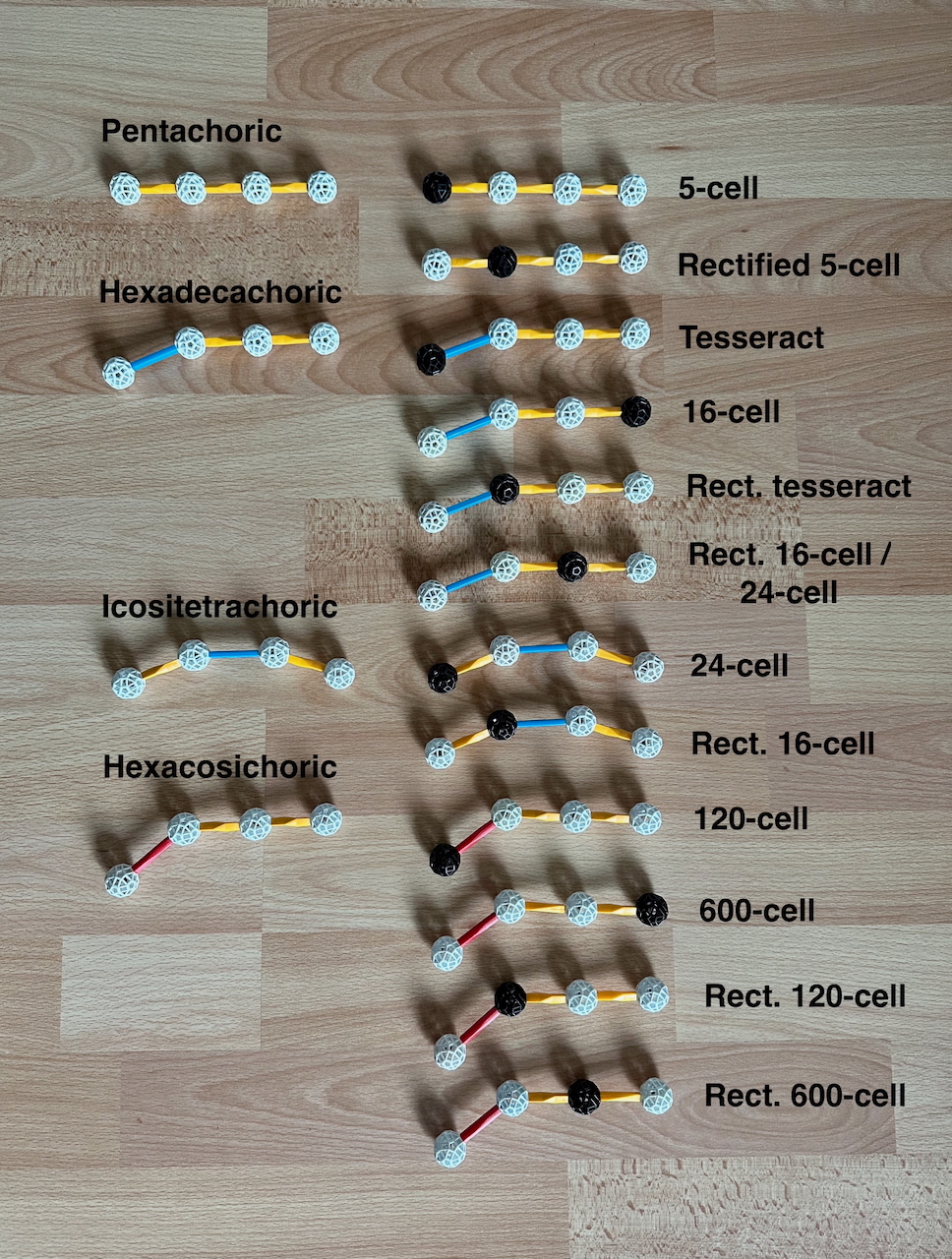
Fig. 9.12a: CD graphs for polychoral kaleidoscopes (on the left), and for the regular polychora and their rectifications built with them (on the right).



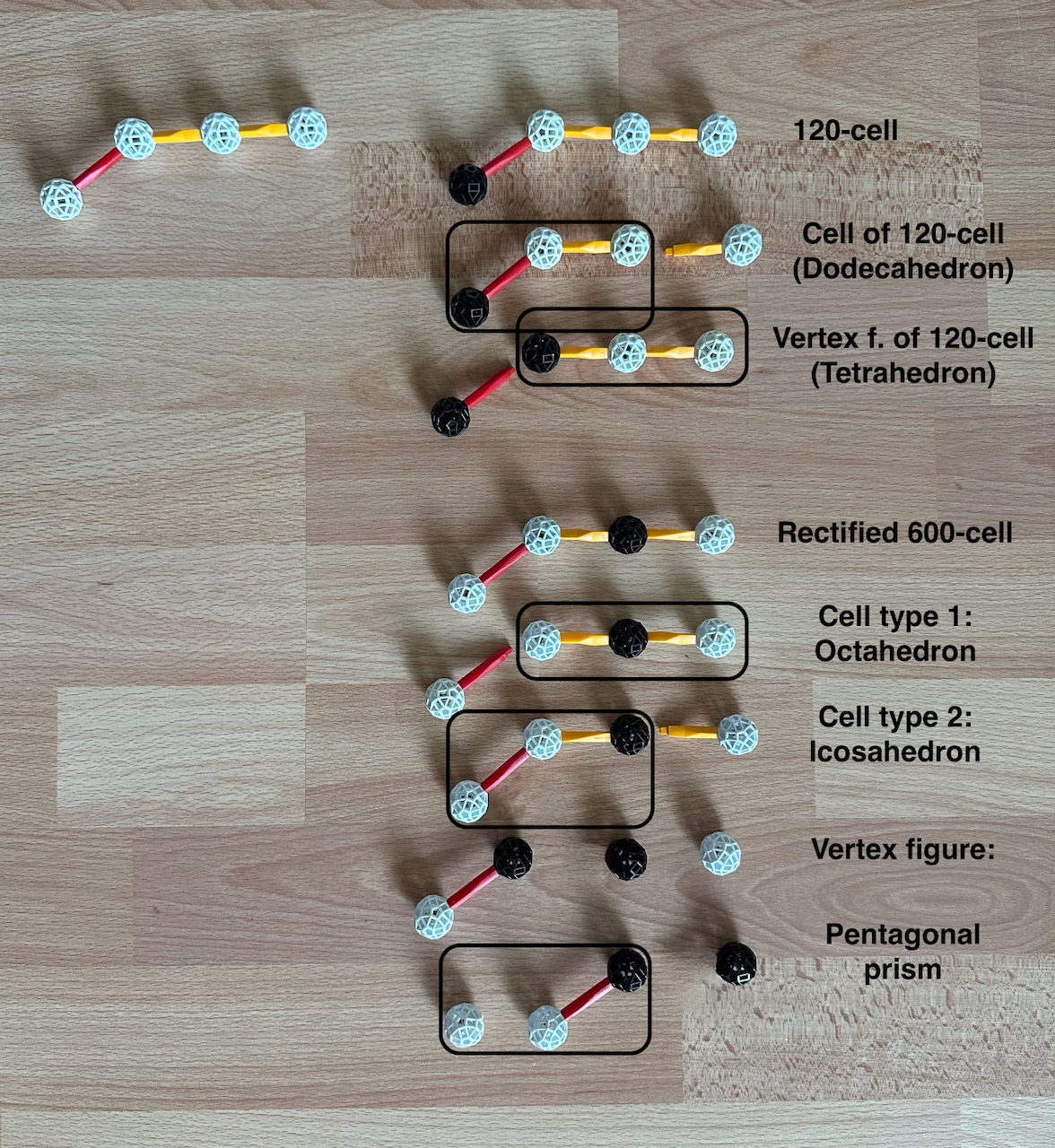
Fig. 9.12b: Example with how to read the cells and vertex figures for the 120-cell and rectified 120-cell.


As before, ringing a single node means that only one mirror is active, i.e., the point being reflected is at the intersection of three other mirrors, which means at one vertex of the Goursat tetrahedron.

Ringing either of the end nodes of the graph represents, in the symmetries in Fig. 9.12a, the construction of two dual regular polychora. For each regular polychoron, we see that the lines in the graph represent the dihedral symmetries of the faces, the vertex figure of the cells and the edge figures. If the CD graph is symmetric (which it is for the Pentachoric and Icositetrachoric symmetries), then the regular polychora obtained from ringing either end are identical (5-cells and 24-cells respectively), this means that they are self-dual. Ringing the middle nodes corresponds to the rectifications. For symmetric graphs the two rectifications are also identical to each other - however, they are not self-dual. Note the two graphs for the 24-cell: this can be obtained as the Rectified 16-cell and also by ringing the kaleidoscope associated with its "native" Icositetrachoric symmetry at one end. This symmetry has no analogue in any other dimensional space.

In Fig. 9.12b, we show how cutting a note at the end opposite to the one being ringed we see the cells of the polychoron: doing this for the CD graph of the 120-cell, we obtain the CD graph of the Dodecahedron. Cutting the ringed node, and ringing the one closer to it, we see the vertex figure; doing this for the 120-cell we obtain the Tetrahedron. For the rectified polychora, we see that there are two types of cells. In the example in Fig. 9.12b, we see that removing alternate nodes of the CD graph of the Rectified 600-cell we obtain the CD graphs of Octahedra (as a rectified Tetrahedron) and Icosahedra. Cutting the ringed node and ringing the next node - in either direction - we see that the vertex figure is a Pentagonal prism (note the similarity with the top CD graph in Fig. 9.11); to do this we need to keep in mind that the two end nodes are linked by an invisible line denoting the 2-fold symmetry. In the last line, we merely rotated the CD graph of the Rectified 600-cell by one node.

***

We now come to a new type of CD graph, one with three branches. This is the graph for the demi-tesseractic symmetry. In Fig. 9.13, we see how this can be derived from the demicubic symmetry of the Tetrahedron.



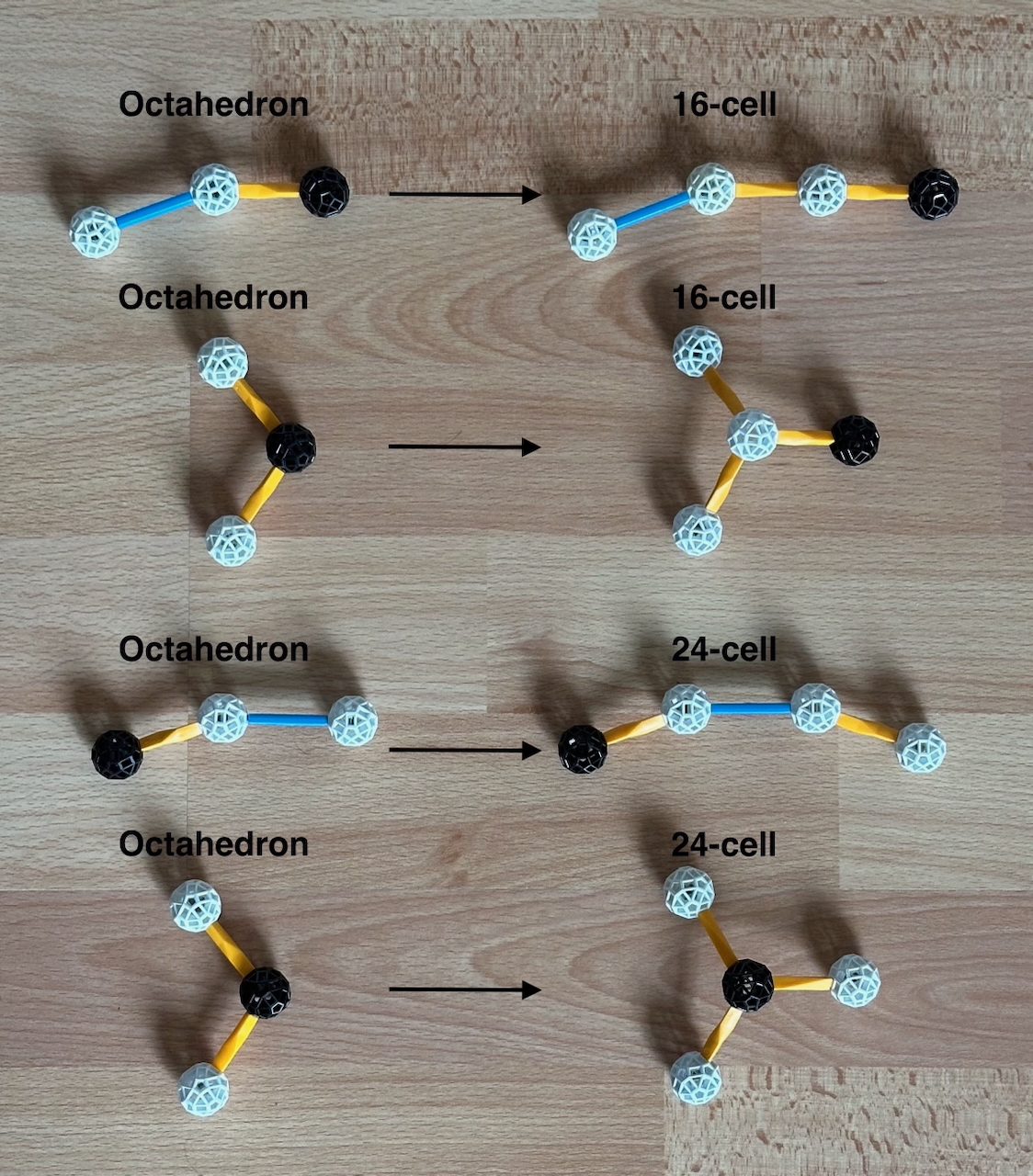
Fig. 9.13: CD graphs for Octahedra and its relatives in four dimensions. The transformations are indicated by the arrows.


At the top, we transform the Octahedron into a 16-cell by adding another node, linking it with a strut with 3-fold symmetry, and ringing the new node instead. Doing this, we obtain the 16-cell. Whenever we add a new node and change the ringing to it, the preceding polytope is the vertex figure of the new one, this means that the Octahedron is the vertex figure of the 16-cell.

Next, we do the same to the Octahedron, but now represent it as a Rectified tetrahedron. Adding one node and strut, we must obtain, again, the 16-cell. Note that, although the polychoron is the same, the underlying symmetry used to build it in this second case (demitesseractic) is not identical to the one used on top (hexadecachoric): as discussed in detail here, the latter can generate uniform polychora with Octagons, because it has a 4-fold strut in its CD graph (as mentioned in Figs. 9.1c and 9.3b, and also 9.10, double ringing leads to a polygon with twice the symmetry); the demitesseractic symmetry has no 4-fold symmetries.

In the third row, we start again with the Octahedron, and add a node at the opposite end instead. It is clear that the Octahedron will be a cell of the new polychoron. A comparison with Fig. 9.12a will show at once that the new polytope is, of course, the 24-cell (it is the only regular polychoron with Octahedral cells), built with its "native" Icositetrachoric symmetry.

In the last row, we do the same, but again with the CD graph of the Octahedron as a Rectified tetrahedron. The result is again the 24-cell, but this time built as a Rectified demitesseract. As we saw in the first and second rows, the demitesseract is the 16-cell, and as mentioned above, the 24-cell is a rectified 16-cell.

***

What is the geometric meaning of the three-fold CD graphs? In the linear CD graphs, ringing a node at either end produces two dual polychora. This duality stems from the fact that the extreme nodes are linked by an invisible 2-fold strut, which indicates a right angle. The edges of two dual polyhedra are perpendicular to each other; the edges and faces of two dual regular polychora are also perpendicular to each other.

In the CD graph of the demitesseractic symmetry, the same is happening, only that this time is the three outer nodes that are connected to each other with three invisible 2-fold struts. This means that the Goursat tetrahedron has three right angles, which are apparent at the centre of a model of this tetrahedron in Fig. 9.14.



Fig. 9.14: Model of the fundamental region of the demitesseractic symmetry. This model is only approximate, since the actual Tetrahedron is a spherical tetrahedron, so the angles at the outer vertices are slightly distorted.


Reflecting either of the three outer vertices in the Wythoff construction, we obtain the vertices of the 16-cell, with half of the length of their edges coinciding with one of the edges of the fundamental region, as for the regular polyhedra and polychora above -- in this case one of the blue struts. The edges of the three 16-cells generated by this symmetry intersect in the connector in the middle. This is the phenomenon of triality we have met when discussing the regular polychoron compounds, see especially Fig. 7.2b on the right. Reflecting the vertex at the centre (using the large Triangular mirror) we obtain the rectification of all three, the 24-cell. As in the case of the polyhedral rectifications discussed above, its edge is inside the fundamental region, linking the vertex at the center with its reflection closer to us. Thus, as in those rectifications, each edge is shared by two neighbouring Goursat tetrahedra. Since the 24-cell has 96 edges, the 3-sphere is covered by 192 of these tetrahedra.

Note than when we choose one of the outer vertices to generate the 16-cell, the symmetry is broken into a bilateral symmetry, with the plane of bilateral symmetry passing through the chosen vertex. Dividing this Goursat tetrahedron in half along that plane we obtain the Goursat tetrahedron for the Hexadecachoric symmetry of the 16-cell, thus 384 of the latter are needed to cover the 3-sphere. When we choose the central vertex to be reflected and generate the 24-cell, the whole figure has 3-fold symmetry. Dividing this tetrahedron along the three planes of bilateral symmetry of the 3-fold symmetry (as in Fig. 9.2b), we obtain six different regions, the Goursat tetrahedra for the Icositetrachoric symmetry of the 24-cell. Thus 6 × 192 = 1152 of those tetrahedra are needed to cover the 3-sphere.


Paulo's polytope site / Next: Beyond the fourth dimension.