Star polychora

The mathematician does not study pure mathematics because it is useful; he studies it because he delights in it and he delights in it because it is beautiful.
J. H. Poincaré

Like polygons or polyhedra, polychora are not necessarily convex. In what follows, we will show models of highly symmetrical non-convex polychora, which are known as ``star polychora'' by analogy with the star polygons and star polyhedra.

To understand many of these polychora, we must clarity the meaning of stellations and facetings among 4-D objects. Stellating a polychoron extends its cells along their 3-D "planes" until they meet identically extended cells, while faceting removes parts of the polychoron while preserving its vertex arrangement.

As for polygons and polyhedra, the larger the number of cells/vertices of a polychoron, the larger the number of its stellations/facetings. All such stellations/facetings are necessarily non-convex.

Also, as for polyhedra, and for the same reasons, if polychora A and B are duals, then the dual of the stellation of A is a faceting of B. It is very important to keep this in mind for understanding what follows.

Regular star polychora

 There are ten regular star polychora, the 4-D analogues of the regular star polyhedra. As for regular star polyhedra, they must be stellations and facetings of regular convex polychora because they must be symmetric around each vertex and around each cell. Below and in Nan Ma's page on star polytopes you can see models of all of them. The cool exploding polychoron animations in the latter site are from this Observable notebook.

All ten have the Hexacosichoric symmetry of the 600-cell and 120-cell; as we'll see below, there are no regular star polychora with other symmetries; this situation is analogous to the regular star poyhedra, which only have Icosahedral symmetry. We depict their geometric relations in Diagrams IIa, b and c below. Some preliminary conclusions from these diagrams: Thus, apart from the Grand 600-cell and Great grand stellated 120-cell, the other 8 regular star polychora are facetings of the 600-cell and stellations of the 120-cell, i.e., they have 120 vertices and 120 cells. Both types of elements are necessarily aligned with the 60 axes of Icosahedral symmetry, with the cells and vertex polyhedra sharing that symmetry. Thus, their cells are necessarily located under their vertices. They are analogous to the Stellated dodecahedron and Great dodecahedron, which are stellations of the Dodecahedron and facetings of the Icosahedron and therefore have 12 faces with 5-fold symmetry located under their 12 vertices; the vertex figures also have 5-fold symmetry.

The icosahedral symmetry of the cells and vertex polyhedra includes central symmetry, for that reason, like the 24-cell, these 8 polychora have both equatorial polyhedra and equatorial cell rings.

***

Three of the regular star polyhedra are built from the 600-cell by using its three sets of regular edge and face sections as cells. Because this faceting operation preserves the edge arrangement, the Zometool representations of their Icosahedral projections are identical to that in Figs. 5.10 and 6.1. Because this is a vertex-first projection, the same is the case for these three projections.


Fig. 6.1: The Zometool Icosahedral projection of the 600-cell, this time seen from a 3-fold symmetry axis. This model also represents the Icosahedral projections of three regular star polychora: the Icosahedral 120-cell, the Great 120-cell and the Grand 120-cell.


The shared edge arrangement of these polychora also implies that their vertex polyhedra must share the vertex arrangement of the vertex polyhedron of the 600-cell: the Icosahedron. This means that they are the three facetings of the Icosahedron depicted in Fig. 4.6c. In cases where the polychora share the same face arrangement, the vertex polyhedra must share the same edge arrangement; their faces are determined by the vertex figures of the cells, their vertex figures are the edge figures of the polychoron. We can therefore fully characterise the star polychora built with the sections of the 600-cell:
  1. The Icosahedral face sections of the 600-cell are the cells of the Icosahedral 120-cell (see virtual model), which shares the Triangular faces of the 600-cell. The vertex polyhedron is the Great dodecahedron, the edge figure is the Pentagram.
  2. Since the Icosahedral 120-cell has Triangular faces, its vertex polyhedron (the Great dodecahedron) must be highlighted by its edges. These are the Great dodecahedral edge sections of the 600-cell and the cells of the Great 120-cell (see virtual model). The vertex polyhedron is the Stellated dodecahedron, the edge figure is the Pentagon. Since the cells and vertex polyhedron are duals, this polychoron is self-dual.
  3. The Dodecahedral edge sections of the 600-cell are the cells of the Grand 120-cell (see virtual model). This polychoron shares the arrangement of Pentagonal faces of the Great 120-cell. Its vertex polyhedron is the Great icosahedron, the edge figure is the Pentagram.
Unlike these regular sections, the equatorial polyhedra in the outermost layer (Icosidodecahedra) do not give rise to additional regular polychora, because they are not themselves regular.

***

We now present Icosahedral projections of the 7 remaining regular star polychora. Like the model of the 600-cell above, these models are made on a φ smaller scale than the corresponding models in David Richter's projects with the Zometool page, the reason for this is the fact that size 3 struts are no longer widely available, but also because the space in my office is limited! Also, they all have points where several blue struts intersect. Because I wanted to make these models a permanent addition to my office, I cut the necessary blue parts with pliers.

Figs. 6.2a, b, 6.3a and b show models of Icosahedral projections of the 6 remaining regular facetings of the 600-cell. Given their symmetry, they necessarily have the vertex arrangement of the Icosahedral projection of the 600-cell (Figs. 5.10 and 6.1). Therefore, as for the three previous regular star polychora, these are vertex-first projections. The Icosahedral symmetry of these projections allows the appearance of undistorted cells and sections (in blue, which we list) that share that symmetry and are located (in 4D) under the two vertices being projected to the centre, at increasing depths.

The first model (Figs. 6.2a and b) represents a projection of the Small stellated 120-cell (henceforth "Stellated 120-cell" for short, see virtual model).


Fig. 6.2a: Icosahedral projection of the Stellated 120-cell and Great grand 120-cell.


Fig. 6.2b: This is how it looks in my office.
Picture by Jason Wu.

How to build: see instructions in David Richter's dedicated page.


The stellation of the 120-cell into the Stellated 120-cell provides an example of how stellations in polychora happen in multiple dimensions: The false vertices of the Stellated dodecahedral cells of the Stellated 120-cell are the true vertices of the Dodecahedral cells of the 120-cell. The same applies to projections: in the projection in Figs. 6.2a and b, the false vertices have the same arrangement (and in this case at the same scale) as the true vertices of the Icosahedral projection of the 120-cell in Fig. 5.11.

Since the vertex figure of the Stellated dodecahedron is a Pentagon and 12 non-overlapping Stellated dodecahedra touch each vertex, the vertex polyhedron of the stellated 120-cell has 12 non-overlapping Pentagons as faces - a Dodecahedron, the edge figure is therefore the Triangle. This is a unique case among the regular polychora and has many consequences described below, the first of which that the edges of this polychoron connect each vertex of the 600-cell to the 20 vertices of the Dodecahedral section closest to it, i.e., section 2 in Table 3. Interestingly, the resulting edges highlight the large Icosahedral vertex sections of the 600-cell, numbers 3 and 5 in Table 3, which were not highlighted by the model of the 600-cell in Fig. 5.10/6.1.

Here is a list of the undistorted polyhedra visible in the model (which you meet as you build the model) which give us a(n incomplete) list of its edge sections:
  1. At the centre, and closest to the vertices, are Great icosahedra, which have the vertices of vertex sections 1 and 7 in Table 3 (more on this below),
  2. The latter's edges are shared with Stellated dodecahedra. These are the cells of the Stellated 120-cell,
  3. The three partially regular polyhedra in Fig. 3.7, which have the vertices of vertex sections 2 and 6 in Table 3 (more on this below),
  4. The latter's edges are shared with Compounds of five cubes (more on this in the discussion on the regular polychoron compounds),
  5. Great dodecahedra. These are the cells of the Great grand 120-cell (see below),
  6. The latter's edges are shared with the aforementioned large Icosahedra, which have the faces of vertex sections 3 and 5 in Table 3. See more on these sections below.
On the outside, enveloping the projection, is an undistorted Dodecadodecahedron, the equatorial polyhedron of the Stellated 120-cell. This shares the vertices of vertex section 4 in Table 3.

There are 120 identical instances of sections 1 to 6, and 60 instances of the equatorial polyhedron. In addition to the 600 Cubes of the Compounds of five cubes, there are also 600 Tetrahedral and 600 Octahedral sections. Thus, the list of sections includes seven of the nine regular polyhedra plus the three partially regular polyhedra. The model shows projections of all instances of these cells, all 600 Tetrahedra and 600 Octahedra are projected with distortion. Note that Sections 1 and 6 are isomorphic, as are Sections 2 and 5. As we've seen, the partially regular polyhedra represented listed in 3) are either isomorphic to each other, or their two sets of faces are isomorphic to each other, as is also the case for Section 7, the equatorial polyhedron.

The Great grand 120-cell (see virtual model) in the list above is built using the Great dodecahedral sections of the Stellated 120-cell as cells. Since these polychora have the same edge arrangement, their vertex polyhedra must have the same vertex arrangement: the Dodecahedron for the Stellated 120-cell, and its only regular faceting, the Great stellated dodecahedron, for the Great grand 120-cell. This means that the edge figure of the Great grand 120-cell is also the Triangle. However, as we've seen in the polyhedron page, the Dodecahedron has many more facetings; one of the consequences of this is the profusion of edge sections, polychora and polychoron compounds that are edge facetings of the Stellated 120-cell, which we will discuss below.

***

The model in Figs. 6.3a and b represents the Icosahedral projection of the Grand 600-cell (see virtual model). The edge arrangement results from connecting each vertex of the 600-cell to the 12 vertices of section 5 in Table 3. Its false vertices have the same arrangement of a φ times smaller 600-cell, the reason for this is explained further below in this page.


Fig. 6.3a: This model represents the Icosahedral projections of the Grand 600-cell and three other regular star polychora that share its edge arrangement.

See also David Richter's page on this projection.


Fig. 6.3b: This is how it looks in my office.
Picture by Jason Wu.

How to build: Make a model of the 600-cell, but extend all internal edges: there can be no broken lines. Then build a new, outer identical set of vertices with the same orientation, with their spacing increased by φ (only a few of these will suffice). For each new outer vertex, see what edges of the internal model point towards it, then extend those edges to the outer vertex. Do this for a set of neighbouring vertices, which will allow you to work out the intersections of those edges. Once this is done, apply the same pattern to all outer vertices using Icosahedral symmetry, while removing all the edges of the outer 600-cell that were holding the outer vertices in place. See rationale for this below.


As mentioned above, the Grand 600-cell is a faceting of the 600-cell and its only stellation; like the latter it has 600 Tetrahedral cells, which have the same orientations of the Tetrahedral cells of the 600-cell. Therefore, the projections of the 600 Tetrahedral cells in the projection in Fig. 6.3a and b are identical to those of the Icosahedral projection of the 600-cell in Figs. 5.10, 6.1 except that they are larger in the former model; all appear distorted in these projections given the latter's Icosahedral symmetry.

Thus, 20 cells and 12 edges meet at each vertex, as in the 600-cell. Thus, since the Grand 600-cell is not convex, its vertex polyhedron has to be non-convex and have 20 Triangular faces and 12 vertices - it is therefore the Great icosahedron. The edge figure is the Pentagram.

As in the case of the 600-cell, the Grand 600-cell has three types of regular edge and face pseudo-sections (thus called because they include regions outside the polychoron they section), with Icosahedral symmetry and 120 instances each, which we list below. In the model in Figs. 6.3a and b two undistorted and superposed instances of each of these sets of pseudo-sections appear under the two superposed central vertices.

As in the case of the 600-cell, these pseudo-sections are the cells of three other regular star polychora that share its edge arrangement, also listed below. Since they have 120 cells, they must be, unlike the Grand 600-cell, stellations of the 120-cell. The shared edge arrangement implies that the Zometool representations of their Icosahedral projections are identical to that in Figs. 6.3a and b. It also implies that vertex polyhedra must share the vertex arrangement of the Great icosahedron (the vertex polyhedron of the Grand 600-cell); this means that they are facetings of the Icosahedron. In cases where the polychora share the same face arrangement, the vertex polyhedra must share the same edge arrangement; their faces are determined by the vertex figures of the cells:
  1. The Tetrahedral cells of the Grand 600-cell imply that its vertex polyhedron (the Great icosahedron) is outlined by its faces. These Great icosahedral face sections, which share their vertices with vertex sections 3 and 5 in Table 3, are the cells of the Great icosahedral 120-cell (virtual model), which therefore shares the Triangular faces of the Grand 600-cell. Since the faces are shared with those of the previous polychoron, the vertex polyhedron must share the edges of the previous vertex polyhedron (the Great icosahedron), it is therefore the Stellated dodecahedron, which means that the edge figure is the Pentagon.
  2. Since the Great icosahedral 120-cell has Triangular faces, its vertex polyhedron (the Stellated dodecahedron) must be highlighted by its edges. These Stellated dodecahedral sections, which share the edges and vertices of the Great icosahedral sections mentioned above, are the cells of the Grand stellated 120-cell (virtual model). The vertex polyhedron must have Pentagonal faces, it is the Great dodecahedron, thus the edge figure is the Pentagram. Since the cells and vertex polyhedra are duals, this is a self-dual polychoron.
  3. The Pentagrammic faces of the previous sections are shared by Great stellated dodecahedral edge sections. Their vertices are those of vertex sections 2 and 6 in Table 3. These are the cells of the Great stellated 120-cell (virtual model), which therefore shares the faces of the Grand stellated 120-cell. Since the faces are shared with the previous polychoron, the vertex polyhedron must share the edges of the previous vertex polyhedron (the Great dodecahedron), its faces are the Triangular vertex figures of the cells: it is therefore the Icosahedron and edge figure is the Pentagon.
On the outside, enveloping the projection, is an undistorted Great icosidodecahedron, the projection of one of the 60 instances of the equatorial polyhedron of the Grand 600-cell.

***

It is an interesting fact that all rectifications of regular polyhedra occur as equatorial polyhedra of all regular polychora with centrally symmetric vertex polyhedra. Here is a list with their (even-sided) equatorial polygons first:

Eq. PolygonEq. PolyhedronPolychora R0/ℓ Figure
SquareOctahedron16-cell √2/2 5.4
HexagonCuboctahedron24-cell 1 5.5a, b
DecagonIcosidodecahedron600-cell, Icosahedral 120-cell, Great 120-cell, Grand 120-cellφ5.10, 6.1
HexagonDodecadodecahedronStellated 120-cell, Great grand 120-cell16.2a, b
DecagramGreat icosidodecahedronGreat stellated 120-cell, Grand stellated 120-cell,
Great icosahedral 120-cell, Grand 600-cell.		1 / φ6.3a, b

The equatorial polyhedra of the facetings of the 600-cell are either the latter's equatorial polyhedron, the Icosidodecahedron, or its facetings (Fig. 4.12). As discussed above, they are useful for calculating the metric properties of their polychora: the values of R0 and R1 for these polychora are those of their equatorial Polygons listed in Table 1 (R0, listed again here). This implies in particular that the Stellated 120-cell and the Great grand 120-cell are, like their equatorial Polygon (the Hexagon) and polyhedron (the Dodecadodecahedron), radially equilateral! This concludes the list of regular polytopes in n dimensions with this characteristic, which already included, apart from the Hexagon, the Tesseract and 24-cell.

We will come back to these useful equatorial polyhedra a couple more times.

***

In Figs. 6.4a and b, we present the Icosahedral projection of the last of the regular star polychora, the most complex of the 16 regular polychora, the final regular stellation of the 120-cell and its only regular faceting: The Great grand stellated 120-cell (virtual model). Since it is the dual of the Grand 600-cell, it has 600 vertices with Tetrahedral vertex polyhedra, and 120 Great stellated dodecahedra as cells.


Fig. 6.4a: Icosahedral projection of the Great grand stellated 120-cell, here seen from a 5-fold symmetry axis.

See also David Richter's page on this projection.


Fig. 6.4b: Same model as in the Figure above, here seen from a 3-fold symmetry axis.

How to build: Make a smaller version of the Stellated 120-cell (in Fig. 6.2a), but with all internal edges extended - there can be no broken lines. Then identify the equivalent vertices of the largest possible Dodecahedron in the model, i.e., the outermost balls along the 3-fold symmetry axes. These are the vertices of the central Dodecahedron of a (large) Icosahedral projection of the 120-cell. Now, based on this, build a few of the remaining "outer" vertices of that projection of the 120-cell at an appropriate scale. Then, from each of those vertices, see what edges in the inner model point towards it, and extend those edges until they reach that vertex. Doing this for a set of neighboring vertices will then allow you to figure out the network of edge intersections. Once this is done, repeat for all vertices of the 120-cell using Icosahedral symmetry, while removing all edges of the large projection of the 120-cell that were holding the first set of outer vertices in place. Look here for the justification of this method of construction.

This model can use 20 Y3 struts. These will be directly aligned with the 3-fold symmetry axis shown in this Figure. This saves 40 regular-sized struts (Y2 and Y1) and 20 balls and slightly improves the appearance of the model. In this model, I omitted intersecting blue struts.


Since the model in Figs. 6.4a and b is an Icosahedral projection of a faceting of the 120-cell, its vertex arrangement is necessarily the same as for the Icosahedral projection of the 120-cell in Fig. 5.11. This also means that, like that projection, this is necessarily a cell-first projection: Indeed, there are two superposed, undistorted Great stellated dodecahedra concentric with the model.

As in the 120-cell, apart from the cells we see no edge sections because there are no Triangular faces; there are no equatorial polyhedra because the vertex polyhedron (the Tetrahedron) has no central symmetry. However, as in the 120-cell, there are equatorial rings with 10 cells, which result from their central symmetry.

Apart from the large number of vertices (600), this polychoron has a great number of false vertices: an inner set with the vertex arrangement of a small 120-cell, a slightly larger one with the arrangement of the 600-cell (together these are the false and true vertices of the Stellated 120-cell), and a second, larger set that also has the arrangement of the 120-cell. As we will see later, these are the vertices of the Compound of 120 5-cells. As shown by the construction method, and discussed in more detail later, these represent successive stages of extension of the edges of the 120-cell.

Geometric relations of the regular polychora

 We will now summarise the properties of the regular polychora. In this summary, we will also show that there are no additional regular polychora. We will do this with the help of Table 4, where we list the possible cells and vertex polyhedra.

Unlike Table 2, this Table is finite, since the cells or vertex polyhedra can only be one of the 9 regular polyhedra. However, of the 81 entries, only 25 are logically possible. The reason for this is that the vertex figure of the cell must match the face of the vertex polyhedron. To give an example, if the cell is a Cube (which has a Triangular vertex figure), then the vertex polyhedron must have Triangular faces. These possibilities appear in 4 groups, depending on the vertex figure of the cells: 16 in the Triangular group (yellow), 1 in the Square group (red), 4 in the Pentagonal group (green) and 4 in the Pentagrammic group (Gold). These numbers are the squares of the number of polyhedra with Triangular, Square, Pentagonal and Pentagrammic faces in Table 2.

The convex regular polychora have their names in boldface. For the Nth column with the cell type corresponds in the Nth row a vertex polyhedron that is its dual. This implies that for the objects along the diagonal (not all of them polychora) the cells and vertex polyhedra are duals, these objects are therefore self-dual. Flipping the table around this diagonal, we find dual objects: for instance, the Great grand 120-cell is the dual of the Great icosahedral 120-cell.


Table 4: Regular polychora have, by definition, regular cells and vertex polyhedra. Thus, if we list all possible cells in columns and all possible vertex polyhedra in rows we can enumerate all regular polychora (colored according to the vertex figures of the cells: yellow - Triangles, red - Squares, green - Pentagons, gold - Pentagrams) and all regular honeycombs of the Euclidean (dark gray) and hyperbolic (gray) 3-D spaces. The objects in light gray are not honeycombs, they are degenerate polychora with an infinite number of elements, the reason for this is that they are isomorphic to the honeycombs of 3-D hyperbolic space indicated with the same letters.

Note the similarity of the top left 4 × 4 square with Table 2.


If the vertex polyhedron is convex and the Solid angles of all cells meeting at a particular vertex equal or exceed 4π steradians, then we don't have a finite polychoron, but a regular division of a 3-D space: a honeycomb. In Table 4, we find all five compact regular honeycombs: the self-dual Cubic honeycomb of the Euclidean 3-D space and the four regular honeycombs of 3-D hyperbolic space: the Order-5 cubic honeycomb, its dual, the Order-4 dodecahedral honeycomb and the self-dual Order-5 dodecahedral and Icosahedral honeycombs.

In this process, we see that the closest analogues of polychoral surfaces are honeycombs of 3-Dimensional ``surfaces'', Euclidean and hyperbolic. There is a close correspondence between polychoral ``surfaces" and the finite honeycombs of the 3-D spherical surface, but as for polyhedra, this correspondence is not one-to-one, because of objects like the regular multi-dimensional beach balls.

Without these five honeycombs, we still have 20 objects. To proceed, we rely on the concept of isomorphism. Among regular polyhedra and polychora, this operation changes all Pentagonal elements (either the cell's faces, vertex figures, or edge figures) into Pentagrammic and all Pentagrammic elements into Pentagonal, as necessary in a reciprocal operation. Two isomorphic polychora are topologically identical, sharing the same number of cells, faces, edges and vertices which have, for symmetry reasons, the same arrangements. The same happens for lower-dimensional elements; i.e., they have the same configuration matrix. The four objects indicated with letters in parentheses are not honeycombs (see detailed treatment in Coxeter 1973), however they are isomorphic to the four hyperbolic honeycombs indicated with the same letters. The resulting infinite number of elements implies that, although we might attempt to build polychora with these types of cells and vertex polyhedra, they never close on themselves.

The remaining 16 objects were already mentioned above. There are therefore no additional regular polychora, and therefore no star polychora with symmetries other than that of the 600-cell. Also, no additional facetings/stellations of the 120-cell and 600-cell are regular.

***

We now discuss the geometric relations between the 120-cell, 600-cell and the regular star polychora. Instead of 6 polyhedra shown in Diagrams Ia and b, we now have 12 polychora, in Diagrams IIa, b and c we follow Conway, Burgiel and Goodman-Strauss (1991) and arrange them as the vertices of a Cuboctahedron, which has 12 vertices.


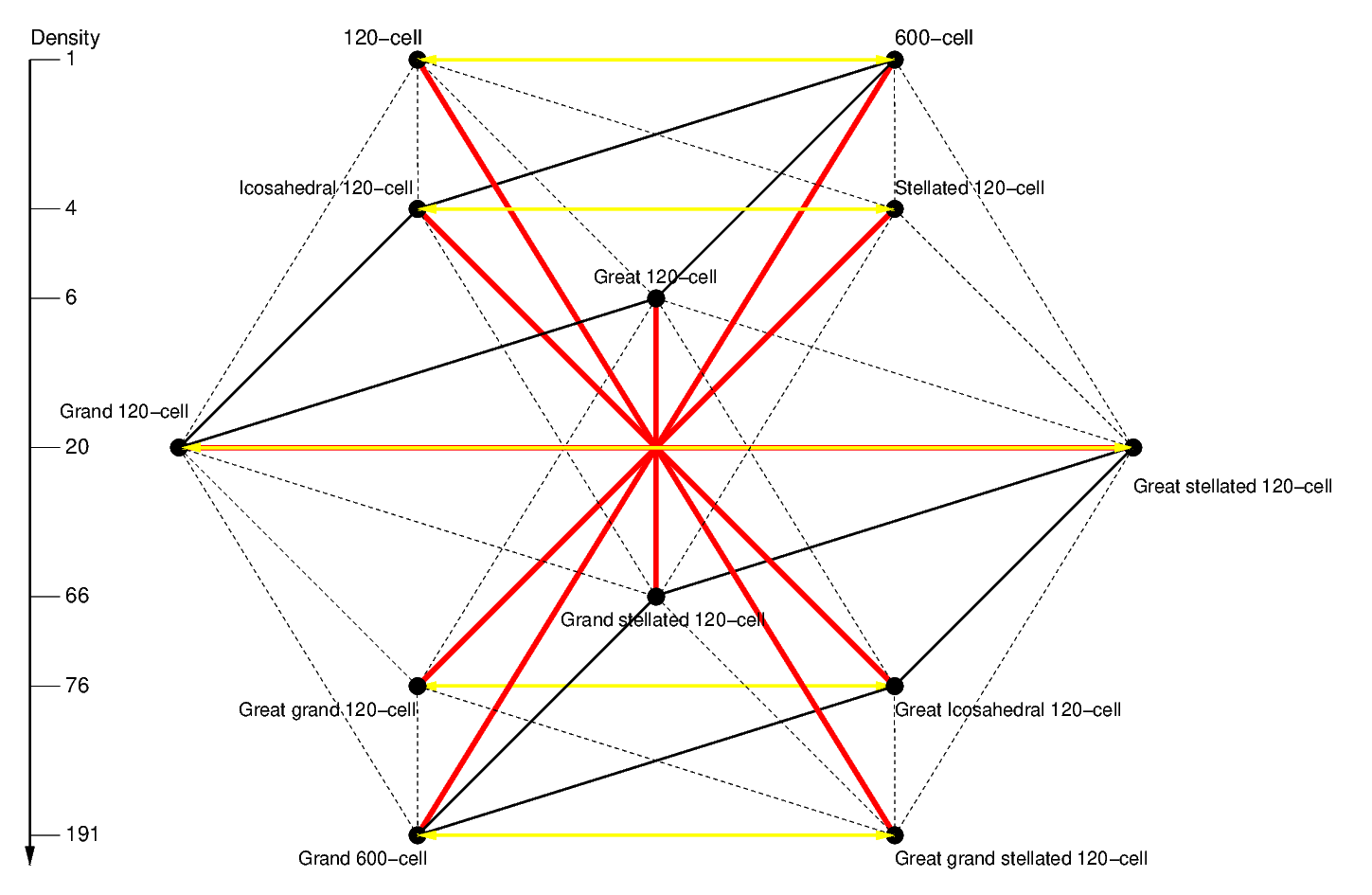
Diagram IIa. Reciprocal relations between the 120-cell, 600-cell and regular star polychora.


As in those earlier diagrams, the vertical scale indicates the density. The thick black lines represent sets of 4 polychora with identical edge arrangements (depicted by the models in Figs. 6.1 and 6.3a and b). The aforementioned reciprocal geometric relations between polytopes are indicated by reflections:
  1. Duality. This operation is represented by the yellow reflections across the central vertical line. The correspondences can be checked from Table 4. Their horizontal direction means that this operation preserves the density. The aforementioned self-dual star polychora, the Great 120-cell and the Grand stellated 120-cell, are necessarily represented in that central vertical line. Other than Polygons and Simplices, they and the 24-cell are the only regular polytopes in n-dimensional spaces with this property.
  2. Isomorphism. This operation is represented by the red reflections through the centre.
To establish these isomorphisms, we note first that the cells and sections of the 600-cell are, respectively, identical and isomorphic to the cells and ``sections'' of the Grand 600-cell (see Diagram Ia). The same applies to their equatorial polyhedra - the Icosidodecahedron and Great icosidodecahedron, both of which share the Triangular faces of their respective polychora. As we've seen, these regular sections are the cells of the regular edge facetings of the 600-cell (Fig. 6.1, in black circuit C) and Grand 600-cell, (Figs. 6.3a and b, in black circuit C'), which are listed below in parentheses.
  1. Tetrahedron - Tetrahedron (600-cell, Grand 600-cell),
  2. Icosahedron - Great icosahedron (Icosahedral 120-cell, Great icosahedral 120-cell),
  3. Great dodecahedron - Stellated dodecahedron (Great 120-cell, Grand stellated 120-cell),
  4. Dodecahedron - Great stellated dodecahedron (Grand 120-cell, Great stellated 120-cell).
Interestingly, their vertex polyhedra (all facetings of the Icosahedron) are also isomorphic (see Diagram Ia):
  1. Icosahedron - Great icosahedron (600-cell, Grand 600-cell),
  2. Great dodecahedron - Stellated dodecahedron (Icosahedral 120-cell, Great icosahedral 120-cell),
  3. Stellated dodecahedron - Great dodecahedron (Great 120-cell, Grand stellated 120-cell),
  4. Great icosahedron - Icosahedron (Grand 120-cell, Great stellated 120-cell),
which, together with their identical cell plane and vertex arrangements implies that the pairs in parentheses are isomorphic to each other! We can also see that the pattern of faceting of the Icosahedral vertex figure of the 600-cell is repeated in reverse (starting in the Great stellated 120-cell) for the facetings of the Grand 600-cell.

As for polyhedra, if two polychora are isomorphic, so are their duals. This is enough to establish the two remaining isomorphisms (120-cell - Great grand stellated 120-cell / Stellated 120-cell - Great grand 120-cell). This can be quickly verified by checking that the vertex and cell plane arrangements in each pair are identical and that their cells and vertex polyhedra are indeed isomorphic to each other, as discussed following Figs. 6.2a and b, 6.4a and b.


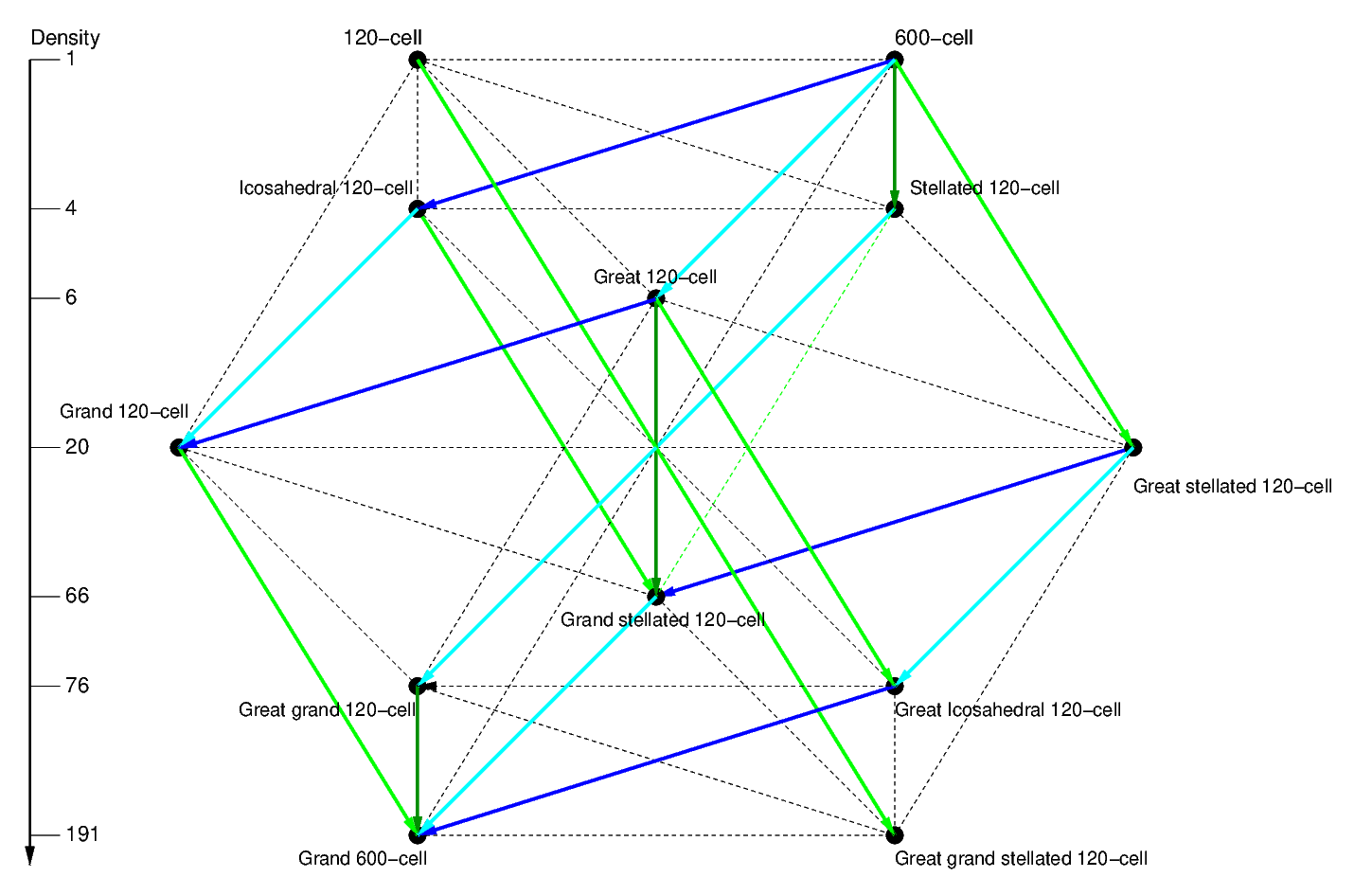
Diagram IIb. Faceting operations for the regular star polychora.

Diagram IIb systematises what we have learned above about the the edge sections of the 600-cell, Grand 600-cell and Stellated 120-cell and the polychora derived from them using these sections as cells. The four faceting operations that occur among regular polychora are represented by parallel translations within the same Cuboctahedral arrangement (represented by arrows), the reason for this is the central symmetry of the isomorphism operation in Diagrams Ia and IIa:
  1. Face faceting. As we've seen from the study of the sections, several polychora share the same face arrangements. These polychora are linked by the dark blue arrows. This operation changes Pentagonal edge figures into Pentagrammic ones
  2. Edge faceting. Equally, we have seen that several polychora share the same edge arrangement, but without sharing face arrangements. These are indicated by the light blue arrows. This transformation preserves the edge figures, but being a faceting operation, it decreases their size.

    As we've seen in the study of the sections, because these two operations preserve the polychoron's edge arrangement, they necessarily facet the vertex polyhedra. In the case of circuits C and C' (here in blue), they are the Icosahedron and its facetings (Fig. 4.6c), which occur in the same sense (top right to lower left) and with the same vertex polyhedra in both circuits. This leads us to the next faceting operation.
  3. Vertex faceting. The light green arrows represent a faceting that preserves the type of vertex polyhedron; however, since this is a faceting, it necessarily reduces the size of the vertex polyhedron: the vertex polyhedron of the 600-cell is an Icosahedron with edge length 1 (the chord of the inner angle of the Triangle), the vertex polyhedron of the Great stellated 120-cell is an Icosahedron with edge length 1 / φ (the chord of the inner angle of the Pentagram).
  4. Dual vertex faceting. This operation, represented by the dark green arrows, is necessary to completely account for all facetings. It transforms the vertex polyhedron into its dual, while reducing its size. Thus, the aforementioned Dodecahedral vertex polyhedron of the Stellated 120-cell is the dual of the Icosahedral vertex polyhedron of the 600-cell.
The latter operation is natural, in the sense that the vertex faceting of a polyhedron replaces a face by a dual one, which for Polygons means an identical one, only rotated. When vertex faceting a polychoron, the faceting either produces dual or identical cells, not both at the same time.



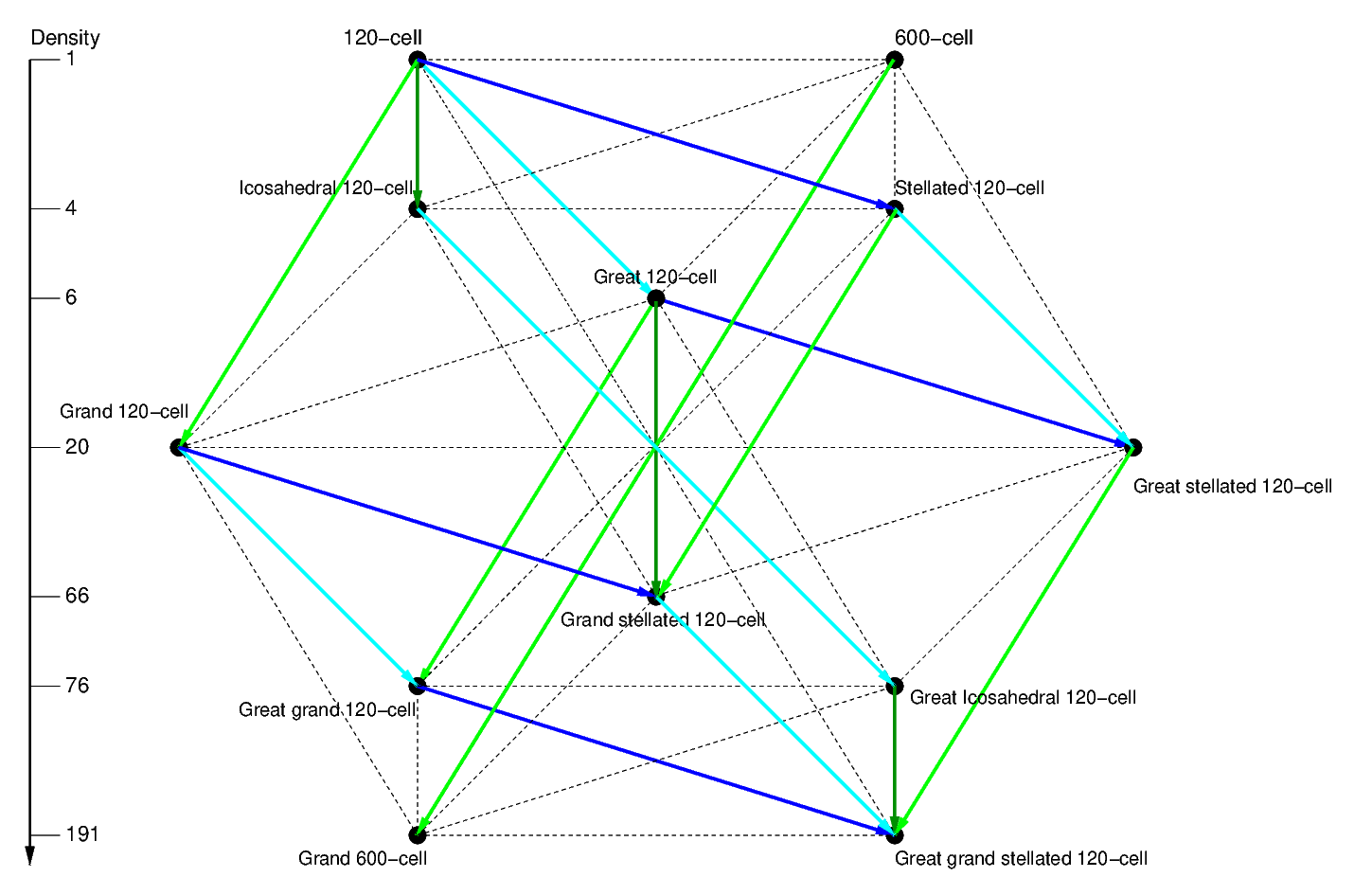
Diagram IIc. Stellation operations for the regular star polychora.


As we've seen, for two dual polychora A and B, a stellation of A (sA) is the dual of a faceting of B (fB). We can therefore say that the stellation operation from A to sA is the dual of the faceting operation from B to fB. Being the duals of the faceting operations, these operations are, in this diagram, a reflection around the central vertical line of the faceting operations in Diagram IIb; for this reason they are also represented by sets of parallel translations, in this case arrows with the same colours as those of their dual transformations. These stellation operations give the regular star polychora their names.
  1. Edge stellation. This operation is represented by the dark blue arrows. Since the dual operation (face faceting) preserves the face arrangement, this operation preserves the dual (perpendicular) edge directions, but extends them, stellating Pentagonal faces into Pentagrammic ones. This has to be since the dual operation transforms Pentagonal edge figures into Pentagrammic ones.
  2. Greatening. This operation is represented by the light blue arrows. Since the dual operation (edge faceting) preserves the edge arrangement, this operation preserves the perpendicular 2-D facial planes. Since the dual operation preserves the type of edge figure but makes it smaller, this operation replaces a face by a larger one of the same type (see Fig. 4.5a).

    Since the dual operations facet the vertex polyhedra, these two operations stellate the cells. The pattern of cell stellation in the top blue circuit is shown in Fig. 4.6b.
  3. Aggrandizing. This operation is depicted by the light green arrows. Since the dual operation replaces vertex polyhedra by smaller ones of the same kind, this operation replaces cells by larger ones of the same kind. From this, we see that the cell types in the lower blue circuit are a repeat of the cell types in the top blue circuit.
  4. Dual aggrandizing. The second operation is depicted by the dark green arrows. Since the dual operation changes a vertex polyhedron into a smaller dual, this operation changes a cell into a larger dual.
As we can see in Diagram IIc, two of the polychora in circuit C' are derived from two of the polychora in circuit C by edge stellation (which stellates Pentagons into Pentagrams). This edge stellation explains why the false vertices of the polychora in circuit C' have the same arrangement as the vertices of the 600-cell, as mentioned above. But do the true vertices have the vertex arrangement of the 600-cell, as we assumed above?

To verify this independently, we note that this edge stellation also happens necessarily to the equatorial polyhedron in circuit C, the Icosidodecahedron: as we've seen in the commentary after Fig. 4.12a, extending its edges we obtain the Great icosidodecahedron, the equatorial polyhedron of circuit C'. The fact that the vertices of this equatorial Great icosidodecahedron lie directly above those of the equatorial Icosidodecahedron it stellates implies that the vertices of the polychora in circuit C' lie directly above those of the polychora in circuit C they stellate, i.e., they are also the vertices of a 600-cell in the same orientation, only in a φ times larger configuration that we expect from stellating all Pentagons into Pentagrams. This applies to their projections as well, thus justifying the method of construction of the model of Figs. 6.3a and b by stellation of the model of Figs. 5.10 and 6.1, with the former's vertex arrangement being φ times larger.

Challenge to the reader: As mentioned above, the Cuboctahedron has 4 Hexagons as equatorial Polygons. In Diagrams IIa, b and c, which Hexagons touch polychora where the cells match the polyhedra touched by the Hexagon in Diagrams Ia and b? Do the geometric operations along them match those in Diagrams Ia and b? If not, what are they replaced with?

To help answer this question, we show in the Figure below a representation of Diagrams IIa, b and c in the Zometool.


Fig. 6.5: Representation of diagrams IIa, b and c with the Zometool. Note the similarity with Fig. 4.10c. The difference here is that we only use two of the faceting prisms and include the struts connecting their vertices to the centre. These struts are the same as used for the edges of the the Cuboctahedron; this happens because the latter is radially equilateral.


The black balls - the vertices of the outer Cuboctahedron - represent the 120-cell, 600-cell and the 10 regular star polychora, the struts represent the geometrical operations discussed above. Note how the edge stellation and its dual, the face faceting, are special, being the only operations represented by the blue struts. All others, including duality, can be represented by green struts and include special double-length cases going through the centre of the figure: the isomorphisms.

Partially regular polychora

 Apart from the convex Archimedean polychora and the regular star polychora, we know many more uniform polychora. It is not known if the list is complete or not, but it likely isn't, because hundreds of them have been found since 2020. However, apart from some of the regular star polychora, only four are edge facetings of the regular polychora, and thus represented by the models above. We now list them.

There is one faceting of the 16-cell, the Tesseractihemioctachoron; which is an edge faceting and therefore shares all the Zometool representations of the 16-cell. This polychoron is constructed with the 4 equatorial Octahedra of the 16 cell plus 8 of its 16 Tetrahedra. Since all cells are regular, this is a semi-regular non-convex polychoron. It is the 4-dimensional analog of a its partially regular vertex polyhedron, the Tetrahemihexahedron; the latter is necessarily a faceting of the Octahedral vertex polyhedron of the 16-cell.

The Stellated 120-cell is special because because a) it is radially equilateral and b) it is the only regular polychoron where the vertex polyhedron is a Dodecahedron. This is interesting because, as we've seen, Dodecahedra can be faceted in 22 different ways, this results in 22 edge facetings of the Stellated 120-cell, all radially equilateral, all sharing the same the Zometool representation. As we have also seen above, one of these is another regular polychoron, the Great grand 120-cell, which has the only regular faceting of the Dodecahedron, the Great stellated dodecahedron, as a vertex polyhedron.

Three of these facetings have the ditrigonal polyhedra in Fig. 3.7 as vertex polyhedra:
  1. The Small ditrigonal 120-600-cell has the Small ditrigonal icosidodecahedron as vertex polyhedron and 120 Great icosahedra and 600 Tetrahedra as cells.
  2. The Ditrigonal 120-120-cell has the Ditrigonal dodecadodecahedron as vertex polyhedron and 120 Great icosahedra and 120 Icosahedra as cells.
  3. The Great ditrigonal 120-600-cell has the Great ditrigonal icosidodecahedron as vertex polyhedron and 120 Icosahedra and 600 Tetrahedra as cells.
The names of these three "ditrigonal" polychora are consistent with those of the ditrigonal polyhedra, which indicate the number of the two types of faces separately. These Icosahedral, Great icosahedral and Tetrahedral cells are the aforementioned Icosahedral, Great icosahedral and Tetrahedral sections of the Stellated 120-cell. In addition to sharing the vertex arrangement of the 600-cell and edge arrangement of the Stellated 120-cell, they share an identical face arrangement, a consequence of the fact that their vertex polyhedra, the partially regular polyhedra in Fig. 3.7, share the same edge arrangement. Furthermore, since all faces are Triangular, their vertex polyhedra are necessarily among their edge sections; these are the ditrigonal sections of the Stellated 120-cell mentioned above.

The isomorphisms between these polytopes are the same as for their vertex polyhedra: the Small ditrigonal 120-600-cell is isomorphic to the Great ditrigonal 120-600-cell and the two sets of cells of the Ditrigonal 120-120 cell are isomorphic to each other.

Being edge facetings of regular convex polychora, the Tesseractihemioctachoron and the three ditrigonal polychora are isogonal and isotoxal. Furthermore, their vertex polyhedra are the partially regular polyhedra, all isotoxal and which each edge separating the two types of faces; this implies that these four polychora are also isohedral, with each face (Triangles in all four cases) separating the two types of cells of each object, all of which are regular, and include, in the four polychora, all regular polyhedra with Triangular faces. No other semi-regular polychora come this close to full regularity. For this reason I call them, by analogy with their vertex polyhedra, the ``partially regular'' polychora.

It is important to note that while the Tesseractihemioctachoron and its vertex polyhedron (the Tetrahemihexahedron) are part of an infinite family of partially regular polytopes (the demi-crosses, which have the edges of the cross polytopes and where the vertex polytopes are the n−1 dimensional demi-crosses), the ditrigonal polytopes are, like the regular polytopes with their symmetries, unique to three and four dimensions, being therefore exceptional.


Paulo's polytope site / Next: Zomable regular polychoron compounds. These exist because two of the facetings of the Dodecahedron are regular compounds: the Compound of five cubes and the Compound of ten tetrahedra.