Polyhedra

"Without Geometry life is pointless."
In "King of Infinite Space: Donald Coxeter, the Man Who Saved Geometry", by Siobhan Roberts.

A polygon (plural "polygons") is a finite region of 2-D Euclidean space* bound by at least 3 straight line segments, or edges; these edges meet in pairs, in angles different from 0 and 180 degrees, at an identical number of vertices. These surface elements (henceforth "elements") - in this case edges and vertices - are, together with the inner surface, also part of the polygon.

A Regular polygon (henceforth Polygons) is isogonal and isotoxal. This means that not only are the elements identical (edges of the same length, edge-vertex-edge angles - the "inner angles" - identical), but the polygon looks the same from all elements of a particular type. It follows from this that the polygon has a well defined centre and that all elements of a particular type are equidistant from it. The inner angle of a Polygon with n sides is given by 180 × (n - 2) / n degrees. This is 60 degrees for a Triangle, 90 degrees for a Square and 108 degrees for a Pentagon.

A Polyhedron (plural "polyhedra") is a finite region of 3-D Euclidean space** bound by at least 4 polygons - its "faces" - and at least 6 edges and 4 vertices. Just as its edges link two vertices, faces meet in pairs at its edges. Just as each polygonal face is bond by an equal number of edges and vertices (at least 3 each), edges and faces meet in equal numbers (and at least 3 each) at each vertex, in a way specified by a single polygon, the "vertex figure". These surface elements are, together with the inner volume, also part of the polyhedron.

Regarding the paper models below, the conventions on polyhedral faces are as follows: The equilateral triangles (henceforth Triangles) are yellow, Squares are red, regular pentagons (Pentagons) are green and regular pentagrams (Pentagrams) are gold. The non-regular polygonal faces are blue.

* This is the traditional definition of a polygon. We will not consider here apeirogons, skew polygons, or complex polygons.

** Again, a traditional definition that excludes tesselations, which are infinite divisions of a 2-D Euclidean space - I don't have space in my office for infinite objects.

Regular and quasi-regular convex polyhedra

In a regular polyhedron, all faces and vertex figures are regular. From this, it follows that it is isohedral: the faces are not only identical, but the polyhedron looks the same seen from all of them; this implies, for instance, that the polyhedron has a well defined centre and that all faces are equidistant from it. The same is true for the other types of elements, i.e., the polyhedron is also isogonal and isotoxal.

Regarding their names, we extend the polygonal naming convention to the regular polyhedra: For the regular tetrahedron, we will use simply the capitalised word Tetrahedron, and likewise for Octahedron, Icosahedron, Dodecahedron, etc.

The first models I built represented the five "Platonic solids", the convex regular polyhedra. They have been known at least since the time of the Pythagoreans.

Fig. 2a: The five Platonic solids.
In the foreground is the Tetrahedron.
In the middle row on the left is the Octahedron, to its right is the Cube.
In the background, on the left, is the Icosahedron, and on the right is the Dodecahedron.

Fig. 2b: Here are the platonic polyhedra again, this time as dice. Picture by Aris Noutsos.

The Tetrahedron has 4 Triangular faces, 4 vertices where 3 edges and 3 faces meet, i.e., with Triangular vertex figures, and 6 edges; it is an equilateral triangular pyramid. This is the smallest number of elements that any polyhedron can have, making this an analogue of the Triangle in 2 dimensions. It has tetrahedral symmetry.

The Octahedron has 8 Triangular faces, 6 vertices where 4 edges and 4 faces meet, i.e., with Square vertex figures, and 12 edges. One can think of it as two equilateral Square pyramids glued together at their Square bases. The Cube is the most familiar shape of all; it has 6 Square faces, 8 vertices with Triangular vertex figures and 12 edges. The Octahedron and the Cube have the same type of symmetry, called Octahedral symmetry.

The Icosahedron has 20 Triangular faces, 12 vertices with Pentagonal vertex figures and 30 edges. The Dodecahedron has 12 Pentagonal faces, 20 vertices with Triangular vertex figures and 30 edges. The Icosahedron and the Dodecahedron have the same type of symmetry, called Icosahedral symmetry.

One interesting feature of the Platonic solids with Triangular faces is that their vertex figures are inevitably highlighted by their edges. In the case of the Tetrahedron, each vertex has a Triangular figure highlighted as the sides of its opposite face. In the case of the Octahedron, the vertex figure is a Square, which appears as an ``equatorial'' polygon halfway between two opposite vertices, there are therefore three of them in three orthogonal planes. In the case of the Icosahedron, the vertex figure is a Pentagon, one appears around (and under) each of the 12 vertices of the Icosahedron. Each edge and vertex of the Icosahedron is shared by two and five such Pentagons respectively.

If the faces have central symmetry, then opposite edges are parallel. The same will happen to adjacent faces. Thus, in these polyhedra there are equatorial ``rings'' of faces. The only face of a Platonic solid with central symmetry is the Square, and indeed in the Cube we can see three equatorial rings of Squares in perpendicular planes.

***
With the Platonic solids, we can build several interesting compounds. Three of them are presented below, the compound of a Tetrahedron with its dual in Fig. 3a, the compound of an Octahedron and a Cube in Fig. 3b, and the compound of a Dodecahedron and an Icosahedron in Fig. 3c. Note that the edges of the two dual polyhedra intersect in their midpoints, indicated by the black balls, at right angles.

Fig. 3a: Zometool edge model of the compound of a Tetrahedron (edges in green) with a dual Tetrahedron (edges in teal).

Fig. 3b: Zometool edge model of the compound of a Octahedron (edges in green) and a Cube (edges in blue).

Fig. 3c: Zometool edge model of the compound of a Icosahedron (edges in yellow) and a Dodecahedron (edges in blue).

The models in these figures were made for illustrative purposes only, they have been disassembled.

These compounds illustrate a concept that will be fundamental for understanding all polytopes, duality.

If polygons A and B are dual, then to a vertex of A corresponds an edge of B, and to each vertex of B corresponds an edge of A. Thus, A and B are of the very same kind, but B is rotated relative to A by 180 deg / n, where n is the number of sides of the Polygons.

If polyhedra A and B are dual, then to a vertex of A corresponds a face of B that is the dual polygon of the vertex figure of A, that face of B is in a plane perpendicular to the line from the vertex of A to its centre. Likewise, to a face of A corresponds a vertex of B, with a vertex figure that is the dual of the face of A. The number of edges of A and B are the same, and each edge of A intersects and edge of B at 90 degrees. If A and B are regular, their edges intersect in their midpoints.

As we can see from Fig. 3b, the Octahedron and the Cube are duals. In Fig. 3c, we can see that the Dodecahedron and Icosahedron are also duals. The dual of the Tetrahedron is another Tetrahedron in a different position (Fig. 3a), i.e., the Tetrahedron belongs to a special class of polyhedra that are self-dual. We can also see that the equatorial Square of the Octahedron is the dual of the equatorial ring of Squares of the Cube - the four vertices of the former correspond to the four faces of the latter. Thus, if regular polyhedron A has faces with central symmetry (and thus has an equatorial ring of faces) its dual polyhedron B will have a vertex figure with central symmetry (and an equatorial Polygon).

Fig. 3a illustrates an important fact: by omitting alternating vertices of the Cube, we obtain the vertices of a Tetrahedron. This makes the Tetrahedron the 3-dimensional representative of an infinite family of polytopes built by deleting alternating vertices of Hypercubes, the Demi-hypercubes, which have their unique demi-hypercubic symmetry.

***
In Fig. 4, we see models of the convex polyhedra derived from the (non-convex) polyhedron compounds in Figs. 3b and c: the intersections of their polyhedra and their convex hulls.

Fig. 4: The convex quasi-regular polyhedra and the rhombic polyhedra.
Bottom left: the Cuboctahedron. To its right is the Rhombic dodecahedron.
Top left: the Icosidodecahedron. To its right is the Rhombic triacontahedron.

The Cuboctahedron is the intersection of the two polyhedra in Fig. 3b. Its vertices are the black balls of that model. Given the way it is built, it has the 6 Square faces of the Cube, the 8 Triangular faces of the Octahedron, 12 identical vertices and 24 identical edges. The Rhombic dodecahedron is the convex hull of the two solids of the compound in Fig. 3b; its vertices are the full set of white balls of that compound. It has 12 identical Rhombic faces (hence its name), the 6 vertices of the Octahedron (with Square vertex figures), the 8 vertices of the Cube (with Triangular vertex figures) and 24 identical edges. These polyhedra share the Octahedral symmetry of the compound from which they were derived.

The Icosidodecahedron is the intersection of the two polyhedra in Fig. 3c, its vertices are the black balls of that model. It has the 20 Triangular faces of the Icosahedron, the 12 Pentagonal faces of the Dodecahedron, 30 identical vertices and 60 identical edges. The Rhombic triacontahedron is the convex hull of the compound in Fig. 3b. Its vertices are the full set of white balls in that model. Its has 30 identical Rhombic faces (hence its name), the 12 vertices of the Icosahedron (with Pentagonal vertex figures), the 20 vertices of the Dodecahedron (with Triangular vertex figures) and 60 identical edges. These polyhedra share the Icosahedral symmetry of the compound from which they were derived.

These polyhedra illustrate an important geometric operation called "rectification". It consists of marking the mid-points of the edges of a polyhedron (for instance, the black balls in Figs. 3a and b) and cutting off the vertices at those points. This results in a new face, provided those mid-points are co-planar.

The rectification of a regular polyhedron A, (rect(A)), has the following properties:

Faces: Rect(A) has two types of faces. 1) The polygonal faces of A are replaced in rect(A) by their dual polygons (i.e., with that particular rotation); 2) Under the vertices of A, rect(A) has a new face, identical to the vertex figure of A.
Vertices: Since the vertices of rect(A) are the mid-points of the edges of A, their numbers are the same. The vertices of rect(A) are all identical, i.e., rect(A) is isogonal. Each vertex is touched by four edges and four faces, two faces of each type and alternating. Thus, the vertex figure is generally a rectangle, with one of its axes of symmetry aligned with the edges of A.
Edges: The number of edges of rect(A) is twice the number of edges of A. All edges are identical and separate the two types of faces, i.e., rect(A) is isotoxal.
If A and B are duals, Rect(A) = Rect(B). However, this is not true for dimensions higher than 3.

The rectification of the Octahedron and Cube is the Cuboctahedron in Fig. 4, the rectification of the Icosahedron and Dodecahedron is the Icosidodecahedron in Fig. 4. Importantly, if we rectify a Tetrahedron, the polyhedron we obtain has only one type of face (Triangles), which means it is regular: the Octahedron. The consequences of this will appear repeatedly in this and the pages that follow. Because they are isogonal and isotoxal, the Cuboctahedron and Icosidodecahedron are called "quasi-regular".

From this, it might seem that a rectification is the same as the intersection of two dual polyhedra whose edges intersect. That is the case for the rectifications of regular polyhedra, however, in general, the intersections of the edges of two dual polyhedra are not in their midpoints.

One of the characteristics of these rectifications is that they have equatorial polygons, a consequence of the central symmetry of their Rectangular vertex figures. The equatorial polygon is a Square in the case of the Octahedron, a Hexagon in the case of the Cuboctahedron, and a Decagon in the case of the Icosidodecahedron. These polygons make it very easy to calculate the metric properties of their polyhedra like the distance of a vertex to the centre, ₀R as a function of the edge length ℓ:

In a Square, ℓ = √ 2 ₀R, i.e., if ℓ = 1, then ₀R = √ 2 /2. The same applies then to the Octahedron.
The Hexagon is the only convex Polygon for which ℓ = ₀R, i.e., it is radially equilateral. The same applies, then, to the Cuboctahedron!
In a Decagon, ℓ / ₀R = 2 sin(18°) = (√ 5 − 1) /2. The latter number is known as Φ and is the inverse of the Golden ratio (φ), i.e., if ℓ = 1, then ₀R = φ. The same applies then to the Icosidodecahedron.

These equatorial polygons can also be used with some of the previous faces to make new polyhedra, the Hemipolyhedra.

***
Now, each rhombic face of a rhombic polyhedron in Fig. 4, defined in Figs. 3b and c by the white balls, is centred on a black ball (a vertex of a quasi-regular polyhedron). Equally, we see in those Figures that each face of a quasi-regular polyhedron (defined by the black balls) is centred on a white ball. This means, as you might have guessed already, that the quasi-regular and rhombic polyhedra are duals.

Being the duals of the quasi-regular polyhedra, the rhombic polyhedra in Fig. 4 must have the following properties:

Faces: They are isohedral, however, their faces are not regular, but rhombic. These Rhombuses are the duals of the rectangular vertex figures of the quasi-regular polyhedra. Like the latter, these Rhombuses have central symmetry.
Vertices: They are not isogonal: there are two types of vertices, corresponding to the two different types of faces of their duals.
Edges: They are isotoxal, with each edge (same number as the dual, and crossing the edges of the dual at 90 degrees) linking the two kinds of vertices.

Since the quasi-regular polyhedra have equatorial polygons, the rhombic polyhedra have equatorial rings of Rhombic faces. This is inevitable given the central symmetry of those faces.

One way of making a Rhombic dodecahedron is by dividing a Cube into six (non-equilateral) Square pyramids, and attach them by their Square bases to the faces of a second Cube. This operation can be seen as the dual of making a Cuboctahedron by rectification of the Octahedron. This will be important later for understanding the 24-cell, and why 4-dimensional space has so many regular polytopes. This also has an immediate consequence: if, in a filling of 3-D space with Cubes (the Cubic honeycomb) we select half of the Cubes in such a way that the Cubes in each set don't touch each other at their faces (i.e., divide the set into two alternate sets of Cubes), divide the Cubes in one set into 6 Square pyramids and attach those pyramids to the neighbouring Cubes, we can fill the full 3-D space with Rhombic dodecahedra: this is the Rhombic dodecahedron honeycomb.

The faces of the Rhombic triacontahedron are Golden rhombuses.

We could in principle apply other types of truncation operation to the Platonic solids to generate other polyhedra. There are 13 isogonal, non-prismatic convex polyhedra where the faces, though not identical, are all Polygons: these are known as the Archimedean solids. Apart from the Cuboctahedron and Icosidodecahedron, none of the other Archimedean solids is isotoxal.

Star polyhedra

If we relax the condition of convexity, then there are four additional regular polyhedra, known as the Kepler-Poinsot polyhedra, or more simply the regular "star" polyhedra. These admit non-convex regular Polygons (Star polygons) as faces or vertex figures, however, only Pentagrams actually occur. The regular polyhedra with Pentagrammic faces were described in detail by Johannes Kepler. Their duals, with Pentagrammic vertex figures, were found about 200 years later by Louis Poinsot. All of them have 30 edges and Icosahedral symmetry.

Fig. 5a: The four regular "star" polyhedra. Note how the central parts of their faces are hidden inside the models.
Bottom left: the Stellated dodecahedron. Bottom right: the Great dodecahedron
Top left: The Great stellated dodecahedron. Top right: the Great icosahedron.

Fig. 5b: The earliest (1430) known representation of a Stellated dodecahedron, in the floor of St. Mark's Basilica in Venice, by Paolo Ucello. I took this picture in June 2022.

The Small stellated dodecahedron (henceforth "Stellated dodecahedron" for short, see 3-D model here) has 12 Pentagrammic faces and 12 vertices with Pentagonal vertex figures. Its dual, the Great dodecahedron (see 3-D model here), has 12 Pentagonal faces and 12 vertices with Pentagrammic vertex figures.

The Great stellated dodecahedron (3-D model here) has 12 Pentagrammic faces and 20 vertices with Triangular vertex figures. Its dual, the Great icosahedron (3-D model here), has 20 Triangular faces and 12 vertices with Pentagrammic vertex figures.

As mentioned at the start, for regular polygons or polyhedra all vertices are at the same distance from the centre. Thus, the inner vertices of the Pentagram or star polyhedra are "false vertices": edges intersect, but they don't end there. In what follows, we generally refer only to the true, outer vertices. Similarly for the edges of the non-convex polyhedra: two or more faces can intersect at a false edge, but none of those faces is limited by that edge. As an example, for the Great dodecahedron above, only the outer edges are true edges.

Earlier on, we have noticed that, because of its Triangular faces, the Icosahedron has its vertex figure (the Pentagon) highlighted by its edges. Because this Pentagon lies on a single 2-D plane, it represents a cut of the Icosahedron by a 2-D plane that includes these edges, an "edge section". The Great dodecahedron has the same vertices and edges of the Icosahedron, but it has these Pentagonal edge sections as faces; the Pentagonal vertex figure of the latter became Pentagrammic in the former. Equally, since the Great icosahedron also has Triangular faces, its vertex figure (the Pentagram) is necessarily highlighted by its edges. The Stellated dodecahedron has the same edges of the icosahedron, but those Pentagrams as faces, and Pentagonal vertex figures instead of Pentagrammic.

***
We now introduce two very important concepts that are essential for understanding these polyhedra, stellation and faceting.

Among polygons, stellation means extending the edges of a polygon until they meet other similarly extended edges of the same polygon. Each stellation transforms a convex Polygon into a larger star polygon or a polygram (a regular compound of Polygons), but preserves the number of edges. Facetings cut into a polygon, but preserve its vertices. The larger the number of sides/vertices of a polygon, the larger the number of distinct stellations and facetings. Such stellations/facetings are necessarily non-convex.

For polyhedra, things are similar: Stellations extend the polyhedron by extending its faces along their planes until they meet other similarly extended faces; therefore they preserve the number of faces and their facial planes. Facetings remove parts of a polyhedron while preserving its vertex arrangement. The larger the number of faces/vertices of a polyhedron, the larger (in principle) is the possible number of its stellations/facetings. As for polygons, such stellations/facetings are necessarily non-convex.

A very important rule links these operations: If polyhedra A and B are dual, then the dual of a stellation of A, s(A), is a faceting of B, f(B). The reason is simple: the facial planes of A and s(A) are the same, thus the lines perpendicular to those planes - where we find the vertices of their duals - are also the same. Thus, the dual of s(A) must have the same vertex arrangement of B, being therefore its faceting. This rule will be very important to understand all that follows.

The specific stellations and facetings and other detailed geometric relations between the Dodecahedron, Icosahedron and the regular star polyhedra are displayed by the diagrams Ia and Ib below. All the operations depicted preserve the full Icosahedral symmetry. Some preliminary conclusions from these diagrams can already be deduced from the number of vertices and faces mentioned above:

The Great dodecahedron, Stellated Dodecahedron and Great Icosahedron are regular facetings of the Icosahedron, sharing its arrangement of 12 vertices. The Great stellated dodecahedron, the only regular star polyhedron with 20 vertices, is the only regular faceting of the Dodecahedron.
Therefore, the duals of these facetings - The Stellated dodecahedron, Great dodecahedron, and Great stellated dodecahedron are regular stellations of the Dodecahedron, all have 12 faces as indicated by their names. The Great icosahedron, the dual of the Great stellated dodecahedron, is the only regular star polyhedron with 20 faces, it is the only regular stellation of the Icosahedron.

Therefore, two polyhedra (the Stellated dodecahedron and Great dodecahedron) are stellations of the Dodecahedron and facetings of the Icosahedron. Their 12 faces and 12 vertices are necessarily co-aligned with the 6 axes of 5-fold symmetry of the model. Thus, these faces are located "under" the vertices, as we can see in Fig. 5a.

Following Coxeter (1973, see references), in Diagram Ia we arrange these six polyhedra as the vertices of a regular Hexagon, the only convex polygon that is radially equilateral.

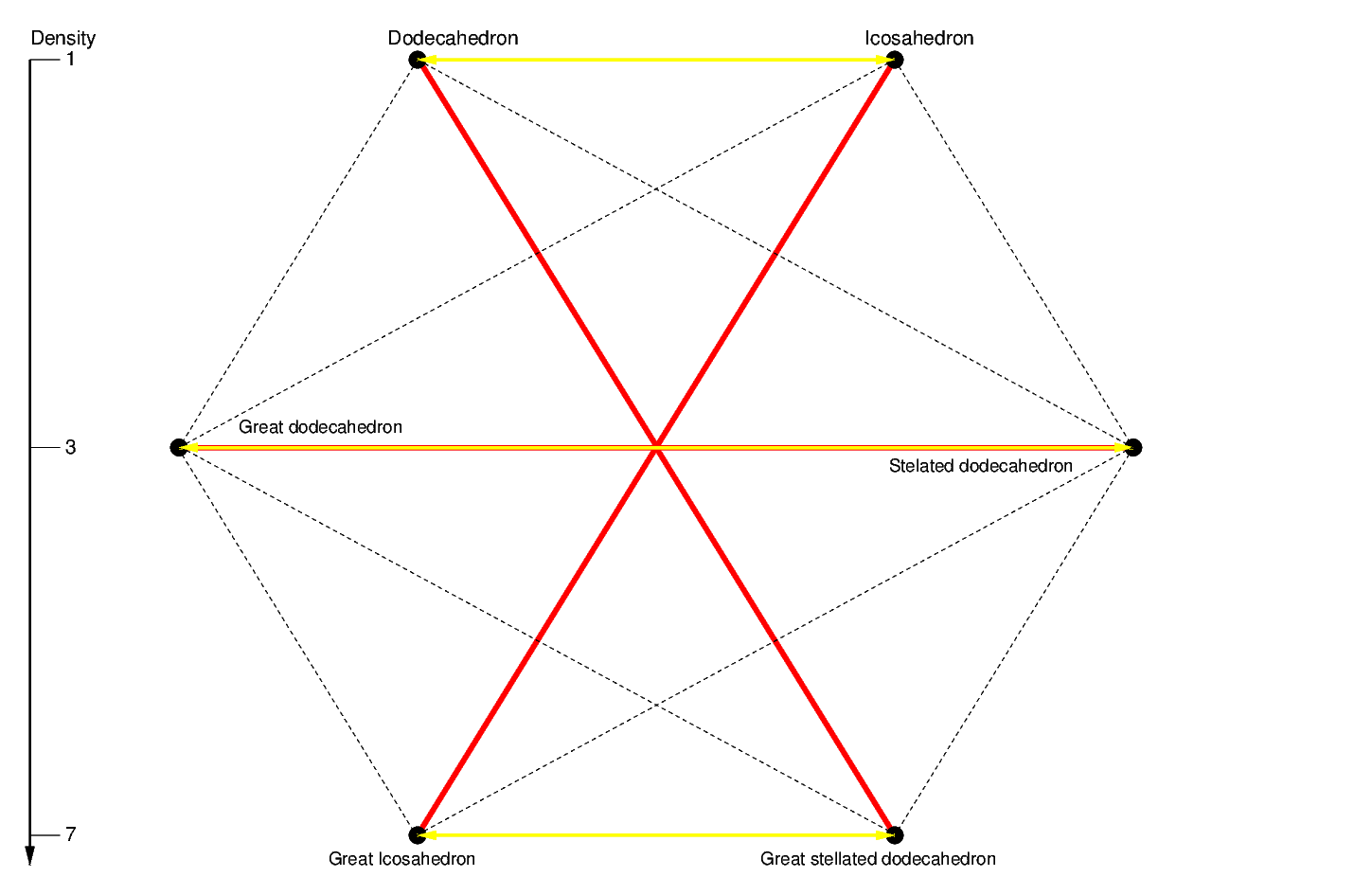
Diagram Ia

The vertical scale indicates the density. The lines denote the two most important geometric relations between polyhedra, both of which are reciprocal (e.g., if A is the dual of B, then B is the dual of A), they are therefore indicated by reflections:

Duality. The operation is represented by the yellow reflections across the central vertical line. Their horizontal direction means that this operation preserves the density.
Isomorphism. This operation is represented by the red reflections through the centre. As pointed out by Coxeter, this operation changes Pentagons into Pentagrams and Pentagrams into Pentagons, whether they are faces or vertex figures. If the polyhedron has Pentagonal and Pentagrammic elements then both must change, otherwise the operation is not reciprocal. Two isomorphic polyhedra are topologically identical: they have the same number of faces, edges and vertices; the faces have the same number of sides, and the vertices have the same number of faces and edges converging into them, etc. (i.e., their configuration matrices are identical).

As an example of isomorphism, the Icosahedron and Great icosahedron are isomorphic, with 20 Triangular faces, five of each join at each of the 12 vertices, which have the same arrangement. They have isomorphic vertex figures (Pentagons and Pentagrams) highlighted by their edges. Thus, using the Pentagons of the Icosahedron to make Great dodecahedra is isomorphic to using the Pentagrams of the Great icosahedron to make Stellated dodecahedra.

If two polyhedra are isomorphic, so are necessarily their duals. This implies that the Dodecahedron is isomorphic to the Great stellated dodecahedron. We have thus established geometrically all the isomorphisms in Diagram Ia.

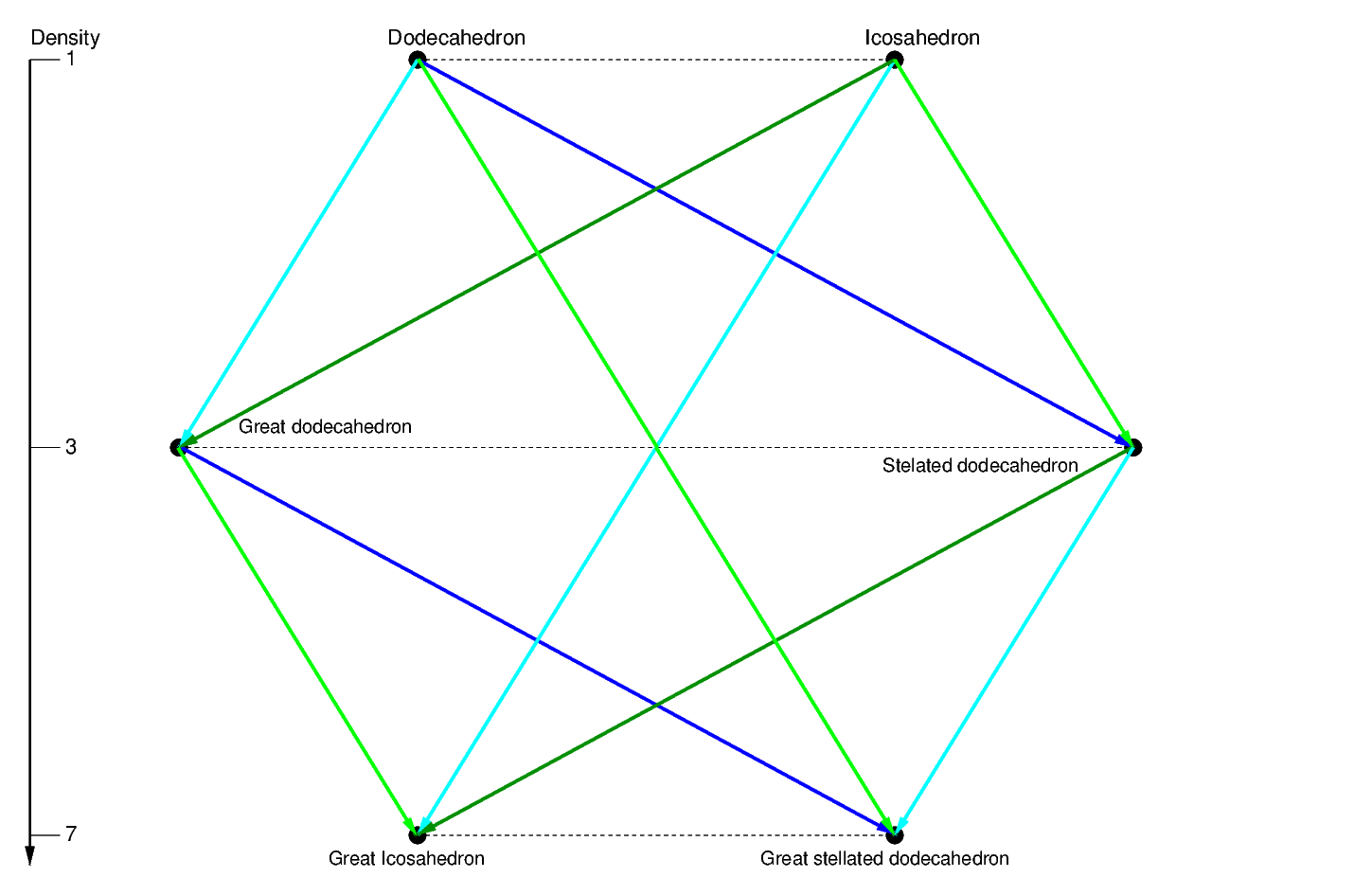
Diagram Ib

Using the information on the sections, we can show, in green in Diagram Ib, the two faceting operations that can occur among regular polyhedra. These can be represented by parallel translations (represented as arrows) within the same Hexagonal arrangement, the reason for this is the central symmetry of the isomorphism operation:

Edge faceting. This operation, represented by the dark green arrows, represents the cases discussed above where the edge arrangement was preserved by making a polyhedron using the sections of another as faces. Because the edges are preserved, this operation necessarily facets the vertex figures, from Pentagons to Pentagrams. In the lower part of the diagram, this operation goes in the opposite direction from the construction of the Stellated dodecahedron from the Great icosahedron; this means that the Great icosahedron is a faceting of the Stellated dodecahedron.
Vertex faceting. This operation, represented by the light green arrows, replaces a vertex figure by a smaller dual. Here we see that the Great stellated dodecahedron is the only faceting of the Dodecahedron, having also Triangular vertex figures.

The four polyhedra in the rectangular green circuit are facetings of the Icosahedron, sharing its vertex arrangement (see Fig. 11c).

As we've seen, for two dual polyhedra A and B, a stellation of A (sA) is the dual of a faceting of B (fB). We can therefore say that the stellation operation from A to sA is the dual of the faceting operation from B to fB. Being the duals of the faceting operations, these operations are, as shown in this diagram in blue, a mirror image of the faceting operations; for this reason they are also represented by sets of parallel translations. These stellation operations give the regular star polyhedra their names.

Edge stellation. This operation is represented as the dark blue arrows. Since the dual operation preserves the edge arrangements but changes Pentagonal vertex figures into Pentagrammic ones, this operation preserves the perpendicular edge directions but extends them by stellating Pentagonal faces into Pentagrammic faces.
Greatening. This operation is represented by light blue arrows. Since the dual operation replaces the vertex figure by a smaller dual, this operation replaces a face with a larger dual in the same plane (see Fig. 11a).

The four polyhedra in the rectangular blue circuit are stellations of the Dodecahedron, sharing its facial planes (see Fig. 11b).

***
We will now summarise the properties of the regular polyhedra. In this summary, we will also show that there are no additional regular polyhedra, despite the fact that that the Icosahedron has many more stellations and the Dodecahedron many more facetings. We will do this with the help of Table 1, where we list the possible faces and vertex figures.

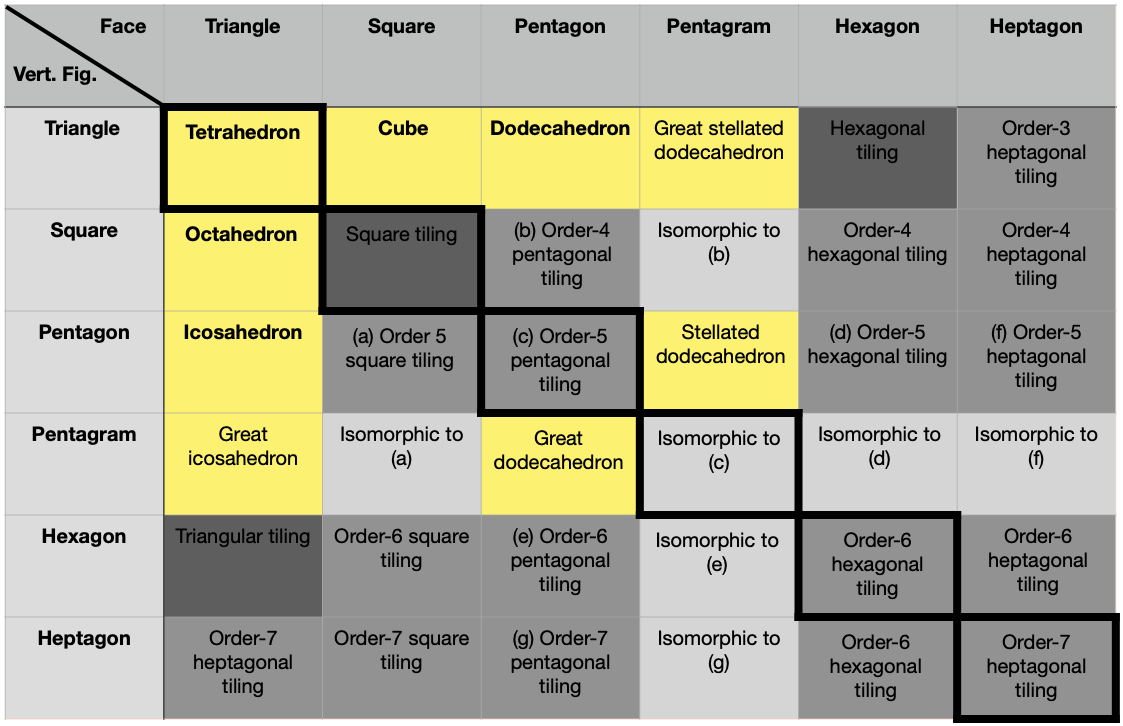
Table 1: Regular polyhedra have, by definition, regular faces and vertex figures. Thus, if we list all possible faces in columns and all possible vertex figures in rows we can enumerate all regular polyhedra (yellow) and regular tilings of the Euclidean (dark gray) and hyperbolic (gray) planes. The convex regular polyhedra have their names in boldface. The objects along the diagonal have identical faces and vertex figures, they are therefore self-dual. Flipping the position of the table around this diagonal, we find dual polyhedra: for instance, the Great stellated dodecahedron is the dual of the Great icosahedron. The objects in light gray are not tilings, they are degenerate polyhedra with an infinite number of elements, the reason for this is that they are isomorphic to the tilings of the hyperbolic plane indicated with the same letters.

That the Platonic solids are the only regular convex polyhedra can be proved very easily by noting that at least three faces must meet at each vertex, and that the sum of the inner angles of those faces must be less than 360 degrees.

Thus, for Triangular faces, the possibilities are the Tetrahedron, Octahedron and Icosahedron. When 6 Triangles meet and a vertex, the sum of the inner angles reaches 360 degrees, and we have the Triangular tiling of the Euclidean plane. For seven Triangles meeting at a vertex, we have the Order-7 triangular tiling, one of the infinitely many regular tilings of the hyperbolic plane.
If three Squares meet at a vertex, we have the Cube, if four Squares meet at a vertex, we reach a sum of inner angles of 360 degrees, thus obtaining the Square tiling of the Euclidean space. Beyond this only hyperbolic tilings with Squares.
If three Pentagons meet at each vertex, we have the Dodecahedron, if four or more meet at a vertex, we have again hyperbolic tilings.
For Hexagons, no polyhedra are possible: if three meet at a vertex, we already have a sum of inner angles of 360 degrees, thus obtaining the Hexagonal tiling of the Euclidean space. Beyond this only hyperbolic tilings exist.

In this process, we see that the closest analogues of polyhedral surfaces are tilings of 2-Dimensional surfaces, Euclidean and hyperbolic. There is a close correspondence between polyhedral surfaces and the finite tilings of a 2-D spherical surface, the spherical polyhedra, but this correspondence is not one-to-one because some types of regular spherical polyhedra have no corresponding regular polyhedra, like the regular beach ball.

That there are no additional regular star polyhedra can be proven in two stages. The first is the argument from symmetry: any star polyhedron must have the vertex and facial plane arrangement as the Platonic solids, because it must also be fully symmetric around its vertices and its faces. If additional symmetric vertex or facial plane arrangements existed, we would have additional Platonic solids. With this argument, we can eliminate polygons with a number of sides larger than 5, either as faces or as vertex figures, leaving a total of 16 possibilities (the top left 4 × 4 subset), 4 of which are, as we've already seen, infinite tilings.

The second stage is based on the idea of isomorphism. The three objects indicated with letters in parentheses are not tilings, however they are isomorphic with the hyperbolic tilings indicated with the same letters. The resulting infinite number of elements implies that, although we might attempt to build polyhedra with these types of faces and vertex figures, they never close on themselves.

The remaining 9 objects were already mentioned above. There are therefore no additional regular polyhedra, and therefore no star polyhedra with symmetries other than Icosahedral.

Rectifications:

We now rectify the four regular star polyhedra. From this, we obtain two quasi-regular star polyhedra (which are uniform) and their duals (which are isohedral).

Fig. 6a: Two quasi-regular star polyhedra and their duals.
Bottom left: the Dodecadodecahedron. Bottom right: Medial rhombic triacontahedron.
Top left: the Great Icosidodecahedron. Top right: the Great rhombic triacontahedron.

Fig. 6b: Here are stained glass models of two quasi-regular polyhedra: the Icosidodecahedron (left) and the Dodecadodecahedron (right). Here we can compare the identical vertex arrangements.
Made by Naomi Janches.

The two rectifications and their duals share all the properties of the convex rectifications and their duals above:

Faces / Vertices: The Dodecadodecahedron is the rectification of the Great dodecahedron and the Stellated dodecahedron. It contains the 12 Pentagonal faces of the former and the 12 Pentagrammic faces of the latter. Its dual is the Medial rhombic triacontahedron, this has 12 vertices with Pentagonal figures and 12 vertices with Pentagrammic figures. The Great icosidodecahedron is the rectification of the Great icosahedron and the Great stellated dodecahedron. It contains the 20 triangular faces of the former and the 12 Pentagrammic faces of the latter. Its dual is the Great rhombic triacontahedron, this has 20 vertices with Triangular figures and 12 vertices with Pentagrammic figures.
Vertices / Faces: They are isogonal, with 30 vertices, as many as the edges of the regular star polyhedra. Four edges and faces (two of each kind and alternating) meet at each vertex, which means that the vertices have Rectangular figures. These vertices are arranged as those of the Icosidodecahedron (see Fig. 6b, 13c). The reason for this can be seen in Diagram Ib: the Stellated dodecahedron can be obtained from the Dodecahedron by a symmetric (both ways) edge stellation. Thus the arrangement of the mid-points of its 30 edges remained unchanged under edge stellation. i.e., it is still the vertex arrangement of the Icosidodecahedron. The same necessarily applies to its dual, the Great dodecahedron. The Great stellated dodecahedron can similarly be obtained from the Great dodecahedron by edge stellation, therefore the mid-points of its 30 edges still have the same arrangement as the Icosidodecahedron. The same necessarily applies to its dual, the Great icosahedron.
This implies that their duals are isohedral, with 30 Rhombic faces which are the duals of the Rectangular vertex figures of the dual polyhedra, also centrally symmetric. These polyhedra are necessarily stellations of the dual of the Icosidodecahedron, the Rhombic triacontahedron (see Figs. 13a and b).
Edges: They are isotoxal, with each of the 60 identical edges separating the two types of faces. This implies that their duals are also isotoxal, with the 60 identical edges linking the two types of vertices.
As we have seen, the Great icosahedron is isomorphic to the Icosahedron. For this reason, the Great icosidodecahedron, the rectification of the Great icosahedron, is isomorphic to the Icosidodecahedron, the rectification of the Icosahedron. The same applies, then, to their duals, the Rhombic triacontahedron and the Great rhombic triacontahedron. In the Dodecadodecahedron, the two types of faces are isomorphic to each other, this means that the same happens for the vertex figures of its dual, the Medial rhombic triacontahedron.

The central symmetry of the Rectangular vertex figures implies (again) that these polyhedra have equatorial polygons. For the Dodecadodecahedron, this is the Hexagon; for the Great icosidodecahedron, this is the Decagram. These equatorial polygons are useful for calculating the metric properties of these polyhedra. The equatorial Hexagon of the Dodecadodecahedron implies that, like the Cuboctahedron above, it is radially equilateral! The equatorial Decagram of the Great icosidodecahedron implies that ℓ / ₀R = 2 sin(54°) = φ, i.e., if ℓ = 1, then ₀R = Φ. These equatorial polygons imply that their duals have equatorial rings of Rhombic faces, which is inevitable given the central symmetry of those faces.

Partially regular polyhedra:

Apart from the regular polyhedra, there are only four uniform polyhedra that are stellations or facetings of the Platonic solids. One of them, the Tetrahemihexahedron, is a faceting of the Octahedron. The other three are the ditrigonal polyhedra. Like the Great stellated dodecahedron, they are facetings of the Dodecahedron. This implies that their duals (which are isohedral) are stellations of the Icosahedron. In Fig. 7 we show models of the ditrigonal polyhedra and their duals:

Fig. 7: Three of the four partially regular polyhedra are known as the ditrigonal polyhedra. They are here shown with their duals:
Bottom left: The Small ditrigonal icosidodecahedron; on top left is its dual, the Small triambic icosahedron.
Bottom middle: Ditrigonal dodecadodecahedron; on top right is its dual, the Medial triambic icosahedron.
Bottom right: The Great ditrigonal icosidodecahedron; on top right is its dual, the Great triambic icosahedron. This is represented by the same model as the Medial triambic icosahedron as they only differ in their internal structure.

Most of their properties are analogous to those of the quasi-regular polyhedra above (this is the reason why they are generally classified as such):

Faces / Vertices: They also have two types of regular faces; in fact each ditrigonal polyhedron has the types and numbers of faces as one of the rectifications with icosahedral symmetry (notice the similarity of the names):
1. The Small ditrigonal icosidodecahedron has 12 Pentagrammic faces and 20 Triangular faces like the Great icosidodecahedron;
2. The Ditrigonal dodecadodecahedron has 12 Pentagrammic and 12 Pentagonal faces like the Dodecadodecahedron,
3. The Great ditrigonal icosidodecahedron has 12 Pentagonal faces and 20 Triangular faces, like the Icosidodecahedron.
Thus, their duals have two types of vertices - in the same numbers and with the same vertex figures as the vertices of the three Rhombic triacontahedra.
Vertices / Faces: They are isogonal; however, instead of 4 edges and 4 faces converging on each vertex as in the quasi-regular polyhedra, 6 edges and 6 faces (three of each kind and alternating) converge on each vertex. Their vertex figures are therefore irregular hexagons with 3-fold symmetry. Their duals are therefore isohedral, with faces that are also irregular hexagons with 3-fold symmetry, which are the duals of the hexagonal vertex figures of the dual polyhedra.
Edges: They are isotoxal, with each edge separating the two kinds of faces; the number of edges is 60, as for the rectifications with Icosahedral symmetry. Therefore, all their duals are also isotoxal, with the 60 edges connecting the two types of vertices. However, in addition, all ditrigonal polyhedra share the same edge arrangement! Therefore, the edges of their duals, which are perpendicular to theirs, share the same edge directions as well, although with different lengths. They can all be derived from the first stellation of the Icosahedron (the Small triambic icosahedron) by a special type of asymmetric edge stellation.
The Small ditrigonal icosidodecahedron is isomorphic to the Great ditrigonal icosidodecahedron. In the Ditrigonal dodecadodecahedron, the two types of faces are isomorphic to each other. This pattern is very similar to that seen among the rectifications with Icosahedral symmetry.

The lack of central symmetry of the vertex figures of these polyhedra implies that, unlike the quasi-regular polyhedra, they have no equatorial polygons. Therefore, in their duals, the faces are not centrally symmetric either, and therefore there are no equatorial rings of faces.

Before ending this section, it is important to remark that the star polyhedra shown above represent only a small fraction of the uniform polyhedra.

Regular and partially regular polyhedron compounds

When stellating or faceting a convex Polygon, we often obtain a compound Polygon, known as a Polygram. Likewise, stellating or faceting a polyhedron often results in polyhedral compounds.

Some of these are themselves fully regular. These must be stellations and facetings of the Platonic solids for the same reason as the regular star polyhedra: because they must also be symmetric around each vertex and around each face. For the same reason, the constituent polyhedra must also be regular; but constructible with a ``smaller'' symmetry contained within the symmetry of the compound. The partially regular compounds are either stellations or facetings of a Platonic solid. Models of all of these are displayed next.

Fig. 8a: The fully regular polyhedron compounds.
In the foreground: the Compound of two tetrahedra, which we have already seen in Fig. 3a.
In the background, left: the Compound of five tetrahedra. On the right is the Compound of ten tetrahedra.

In Fig. 3a, we already saw the Compound of two Tetrahedra, also known as Stella Octangula, is the only stellation of the Octahedron. The Triangular faces of the Octahedron are expanded into dual Triangles that have twice the edge length (see Figs. 10a, b). In Diagram Ib, this type of stellation is called a "greatening". The two Tetrahedra in the compound are dual to each other. Since the compound is self-dual, it is also a faceting of the Cube, the only one. This compound has Octahedral symmetry.

The Compound of five tetrahedra is a faceting of the Dodecahedron, but does does not share its Icosahedral symmetry; it only has rotational symmetry around the symmetry axes, and no mirror symmetry. This is known as Chiral Icosahedral symmetry. This compound has a mirror image that is different from it, i.e., this compound comes in two Chiral forms. The existence of these forms highlights the fact that, generally, stellation and faceting operations do not necessarily preserve the full symmetry of the polyhedra being faceted and stellated.

Interestingly, and very rarely, these forms are dual to each other. Since both are facetings of the Dodecahedron, then both of them must be stellations of the Icosahedron. Indeed, this compound has 20 Triangular faces, like the Icosahedron and Great icosahedron, and 20 vertices with Triangular vertex figures, like the Dodecahedron and Great stellated dodecahedron; like all regular polyhedra with Icosahedral symmetry, it has 30 edges.

The Compound of ten tetrahedra can be seen as the combination of the two chiral and dual Compounds of five tetrahedra, which means it is self-dual and has full Icosahedral symmetry. Alternatively, it can be seen as a Compound of five Stellae octangulae, each made of Tetrahedra from the two dual Compounds of five tetrahedra. Since the 40 vertices of the 10 Tetrahedra coincide in pairs with the 20 vertices of a Dodecahedron, its self-duality implies that the 40 Triangular faces of the ten Tetrahedra fall in pairs on the 20 facial planes of a Icosahedron. It has 60 edges.

***
As we said above, rectifying the Tetrahedron results in another regular solid, the Octahedron. Applying the process to the Compound of two Tetrahedra, we obtain two superposed Octahedra. An inspection of the model shows why this is the case: each new face produced by the rectification of a Tetrahedron is co-planar with a face of its dual Tetrahedron (see Figs. 10a and b).

Applying the rectification to the other Tetrahedral compounds above, we obtain the results below.

Fig. 8b: The partially regular polyhedron compounds.
On the left is the Compound of five octahedra. On the right is its dual, the Compound of five cubes.

In the case of either Compound of five tetrahedra, the rectification results in a Compound of five octahedra. Rectifying the Compound of ten tetrahedra results in two exactly superposed Compounds of five octahedra; the reason is that the Compound of ten tetrahedra can be seen as a Compound of five Stellae octangulae, and as mentioned above, rectifying each of those results in two superposed Octahedra. The dual of the Compound of five octahedra is the Compound of five cubes.

Faces / Vertices: As we've seen above, a rectification of two dual forms has the faces of both of them, but in dual orientations. Therefore, the Compound of five octahedra, being a rectification of both Compounds of five tetrahedra, has (like their combination, the Compound of ten tetrahedra) 40 Triangular faces falling in pairs on the 20 facial planes of the Icosahedron.
This fact means that it is a stellation of the Icosahedron, and therefore partially regular. Thus its dual, the Compound of five cubes, is a faceting of the Dodecahedron and thus also partially regular: like the Compound of ten tetrahedra, its 40 vertices coincide in pairs with the vertices of the Dodecahedron.
Given the vertex coincidences, the latter compound must facet the Compound of five cubes, with each of its five Stellae Octangulae faceting a single Cube. Thus, by duality, it is also a stellation of the Compound of five octahedra.
Vertices / Faces: As for the other rectifications with Icosahedral symmetry, the 30 vertices of the Compound of five octahedra (which are as many as the edges of the Compound it rectifies) are arranged as the 30 vertices of the Icosidodecahedron (see Fig. 13c). Thus as the duals of those rectifications, the Compound of five cubes has 30 faces on the same planes as the 30 faces of the Rhombic triacontahedron (see Figs. 13a and b).
Edges: As in previous rectifications, the rectification of the Compound of five tetrahedra doubled the number of edges; this means that, like all rectifications with Icosahedral symmetry and their duals - and, again, the Compound of ten tetrahedra - the Compound of five octahedra has 60 identical edges. The same is therefore true for all duals, including the Compound of five cubes.
Additionally, the latter compound shares the edge arrangement of three partially regular 60-edge facetings of the Dodecahedron, the ditrigonal polyhedra in Fig. 7. This means, by duality, that the 60 edges of the Compound of five octahedra can be obtained by extending the edges of the first stellation of the Icosahedron, the Small triambic icosahedron, as for the duals of the partially regular polyhedra in Fig. 7.

Summarizing: Being facetings and stellations of the Platonic solids, the compounds in Fig. 8a are fully regular, like the regular star polyhedra in Fig. 5a. Being rectifications of the compounds in Fig. 8a or their duals, the compounds in Fig. 8b share some characteristics with the rectified polyhedra and their duals in Fig. 6a: they are facetings of the Icosidodecahedron or stellations of the Rhombic Triacontahedron. However, in addition, they are also stellations or facetings of the Platonic solids, i.e., they are partially regular like the ditrigonal polyhedra and their duals in Fig. 7, with which they share edge directions. However, since they are are isogonal, isotoxal, isohedral and consist of Platonic solids, they are generally considered regular as well.

***
There are many more non-regular stellations of the Icosahedron: one counting method yields a total of 59 stellations. However, the definition of polyhedra above includes only 22 of these stellations, which include polyhedra (like the Great icosahedron, the duals of the partially regular polyhedra in Fig. 7 and, for instance, the excavated dodecahedron) or three of the regular compounds (of 5 Tetrahedra, 10 Tetrahedra and 5 Octahedra). These 22 stellations have duals that are facetings of the Dodecahedron (see models), which include the Great stellated dodecahedron, the partially regular polyhedra in Fig. 7, the excavated dodecahedron (which is self-dual) and three of the regular compounds (of 5 Tetrahedra, 10 Tetrahedra and 5 Cubes). In contrast, apart from the regular star polyhedra, there are no additional stellations of the Dodecahedron / facetings of the Icosahedron!

We note that many more symmetric polyhedron compounds can be built. One especially interesting class, which includes the objects we just discussed, is the uniform polyhedron compounds.

In what follows, we show some Zometool models that illustrate some of the geometrical relations between the objects we have just presented.