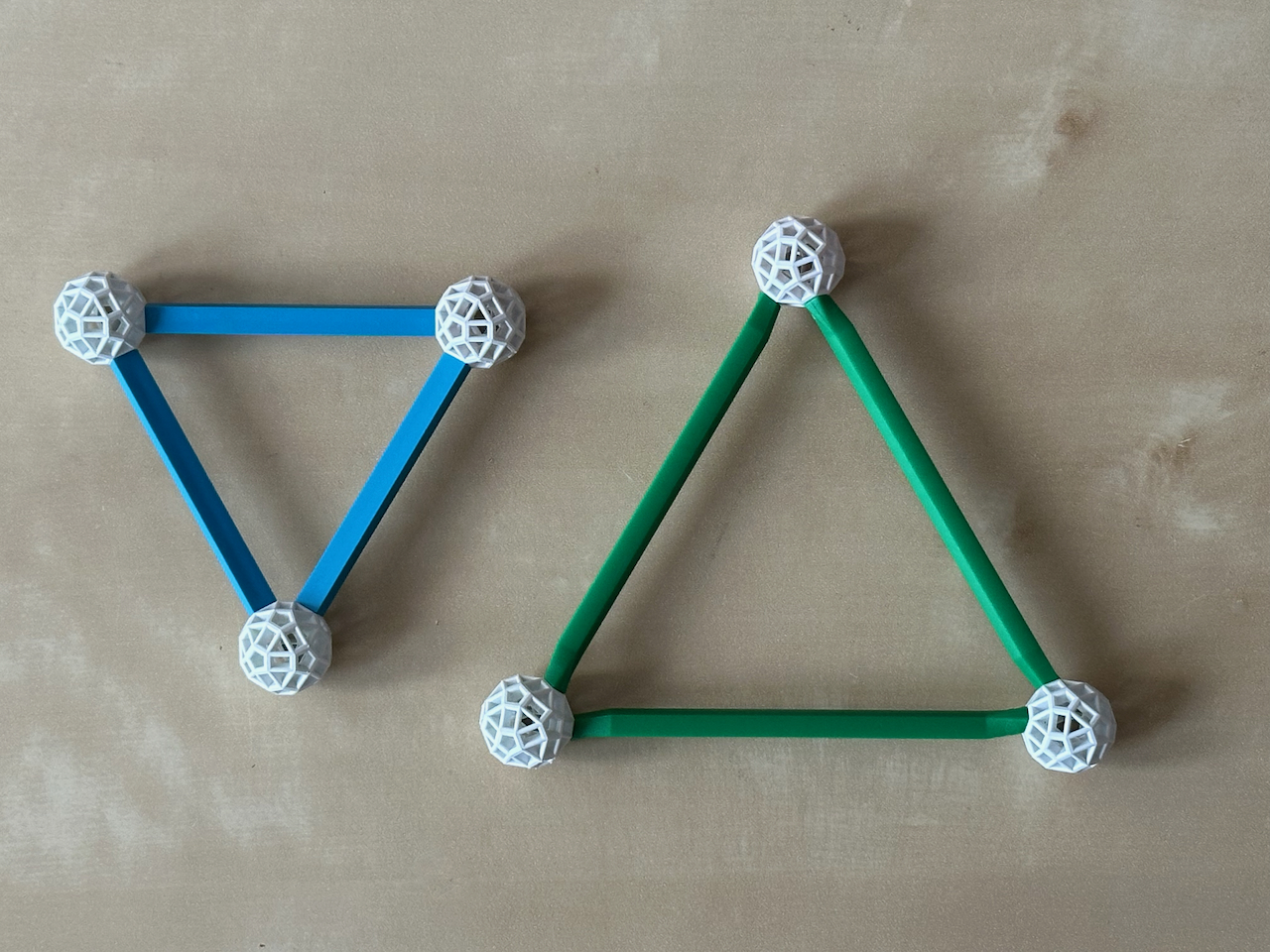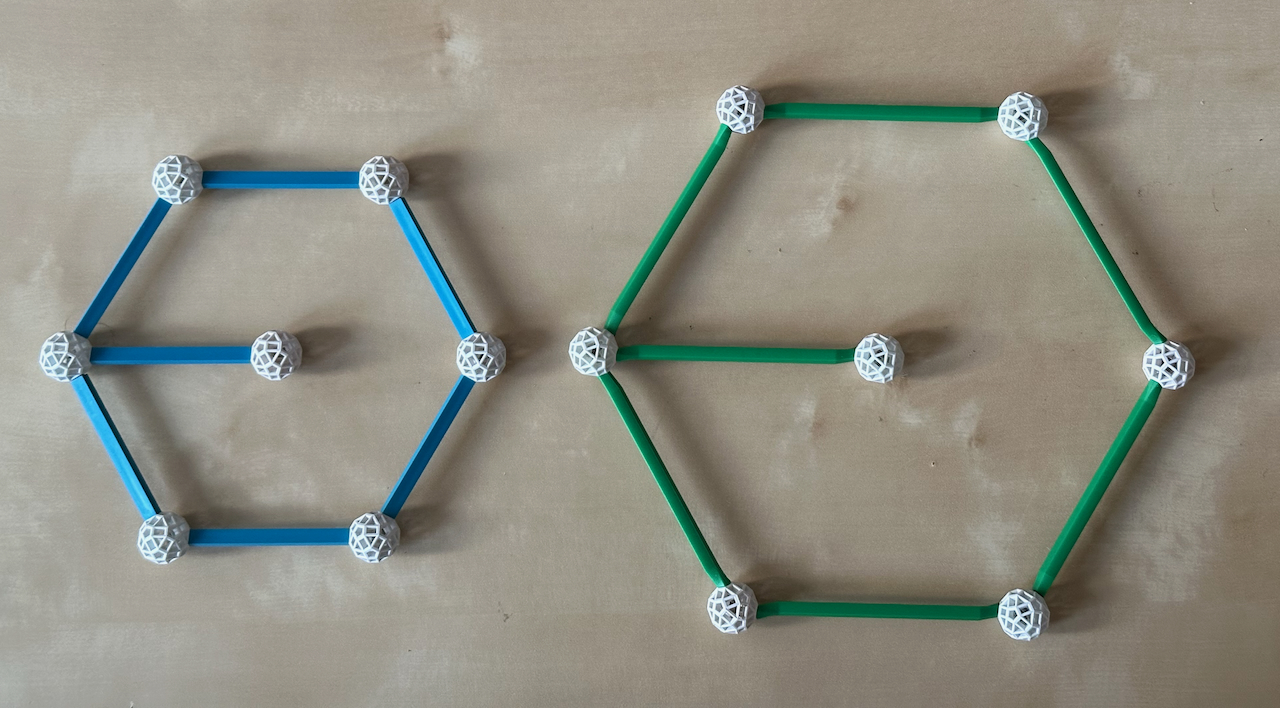Polygons

"Without Geometry life is pointless."
In "King of Infinite Space: Donald Coxeter, the Man Who Saved Geometry", by Siobhan Roberts.

In this site, I will be showing many geometrical models made using the Zometool system, which was developed by Steve Baer, Clark Richert, Marc Pelletier and Paul Hildebrandt. For this reason, I will explain some of its features that will be useful for understanding what follows.

Points, line segments, the Zometool

 In Fig. 2.1, I show the standard components of the Zometool, these represent zero and one-dimensional elements, points and line segments.

Geometry starts with geometric points, of zero dimensions. These are represented in the Zometool by the connectors, all identical: they have 12 Pentagonal holes, 20 Triangular holes and 30 rectangular holes, in a pattern that is similar, but not identical, to the faces of the Rhombicosidodecahedron. They have, therefore, an overall Icosahedral symmetry. They are normally provided in white, as in this Figure, but the Zometool company sells them in a few colours.


Fig. 2.1: The standard components of the Zometool. The balls are in white, the struts are shown for sizes 0, 1 and 2 for the different colours (see explanation below for these).


In geometry, the one-dimensional objects include line segments, which in the Zometool are represented by the struts. These are always identical at both ends: We will keep this B, R, Y, G terminology to indicate the shapes of the struts, even when referring to struts in non-native colours, which are also sold by the Zometool company. The R and Y struts have a twist in the middle, which means that the balls at both ends have always identical orientations. This means that, in any model made with the Zometool, all balls are aligned exactly with each other!

All of these struts come in three regular sizes (n = 0, 1, 2), all shown in Fig. 2.1, with the distance between the centres of balls attached at both ends (which we will designate as its length) of size n being x times larger than for size n − 1 (we will calculate this number x soon). This geometric progression means that any model built in a size could in principle be built in a smaller or larger size. Red struts also have a very short (00) size. Green struts also come in half-sizes (HG), two HG2 struts are shown right at the top of the Figure. Size 3 struts were made by the Zometool company in the early days, but they have been discontinued, and for that reason they are a bit harder to find. I buy them mostly on eBay.

To calculate the lengths of these struts, we will now define the length of the B1 strut as the unit of measurement. Given the geometric progression mentioned above, the B0 strut has length 1/x and the B2 strut has length x.

Fig. 2.1 shows a very important feature of the system: size 2 struts are as long as the sum of the lengths of struts with sizes 0 and 1:

x = 1 + 1/x   (a)

Multiplying both sides by x and moving them to the left, we obtain a simple quadratic equation:

x2 − x − 1 = 0   (b)

Using the quadratic formula, we see that there is a single positive solution to this equation:

x = (√ 5 + 1) / 2 = 1.618 033 988 749 894 848 204 586 834 365...,

which is the Golden ratio, φ. The the other solution to eq. (a) is Φ = −(√ 5 − 1)/2. From equations (a) and (b), we derive:

1 / φ = φ − 1 = − Φ = 0.618 033 988 749 894 848 204 586 834 365...   (c)

φ2 = φ + 1 = ( √5 + 3 ) / 2 = 2.618 033 988 749 894 848 204 586 834 365....   (d),

these are the lengths of the B0 and B3 struts. Equation (d) implies φ = √(φ + 1), we can also use it to calculate all powers of φ (lengths of B4, B5, B6, B7,...):

φ3 = 2 φ + 1 = ( 2 √5 + 4 ) / 2 = 4.236 067 977 499 789 696 409 173 668 731...

φ4 = 3 φ + 2 = ( 3 √5 + 7 ) / 2 = 6.854 101 966 249 684 544 613 760 503 096...

φ5 = 5 φ + 3 = ( 5 √5 + 11 ) / 2 = 11.090 169 943 749 474 241 022 934 171 828...

φ6 = 8 φ + 5 = ( 8 √5 + 18 ) / 2 = 17.944 271 909 999 158 785 636 694 674 925...,

which merely extends what Fig. 2.1 is showing, that each term in the series is the sum of the two previous ones. A consequence of this is the simple expressions in the second column, which imply that any large B strut size can be built by adding as many smaller B1 (unit) and B2 (φ) struts as indicated by the coefficients in boldface. These coefficients are the famous Fibonacci numbers, where the (n + 1)th term in the sequence (Fn + 1) is the sum of the two previous terms, Fn and Fn − 1, the sequence starts with F0 = 0 and F1 = 1. Note that the unit coefficients are one position behind in the sequence relative to the φ coefficients, therefore they can be written for n > 0 as:

φn = Fn φ + Fn − 1 = ( Fn √5 + Ln) / 2,   (e)

where Ln = Fn + 2 Fn − 1 are the coefficients in italic, the Lucas numbers. Using eqs. (c) and (d), we can calculate the negative powers of φ (lengths of B−1, B−2, B−3, B−4, B−5, ...):

φ−2 = − 1 φ + 2 = ( − 1 √5 + 3 ) / 2 = 0.381 966 011 250 105 151 795 413 165 634...

φ−3 = + 2 φ − 3 = ( + 2 √5 − 4 ) / 2 = 0.236 067 977 499 789 696 409 173 668 731...

φ−4 = − 3 φ + 5 = ( − 3 √5 + 7 ) / 2 = 0.145 898 033 750 315 455 386 239 496 903...

φ−5 = + 5 φ − 8 = ( + 5 √5 − 11 ) / 2 = 0.090 169 943 749 474 241 022 934 171 828...

φ−6 = − 8 φ + 13 = ( −8 √5 + 18 ) / 2 = 0.055 728 090 000 841 214 363 305 325 074...

As for positive powers, each power and its associated coefficients is the sum of the two previous powers and their associated coefficients. The coefficients in boldface and italic are the Fibonacci and Lucas numbers, only that their signs alternate (these are the Fibonacci and Lucas sequences extended to negative integers) and the unit coefficients in boldface are one position ahead in the Fibonacci sequence relative to the φ coefficients. Thus, for n > − 1:

(− φ)− n = Φn = − Fn φ + Fn + 1 = (− Fn √5 + Ln) / 2,   (f)

where we used the relation Ln = − Fn + 2 Fn + 1. In the limit of very large values of n, Φn converges to zero and

φ = Fn + 1 / Fn,   Ln / Fn = √5.

The convergence of the ratio of two successive terms of the Fibonacci sequence to φ, which was first demonstrated by Kepler, implies that the same happens for all sequences of positive reals where each term is the sum of the two previous ones, like the Lucas numbers.

***

As an aside, these powers of φ yield, in a simple way, many exact relations between the Fibonacci and Lucas numbers. For a few examples, adding (f) to (e), we obtain an equation that allows the calculation of the Lucas numbers without the need to know all previous terms in the sequence. Subtracting (f) from (e), we obtain a similar equation for the Fibonacci numbers, Binet's formula:

φn + Φn = Fn − 1 + Fn + 1 = Ln,     (φn − Φn) / √5 = Fn.     (g)

The first equation implies that for |Φn| < 0.5 (i.e., n > 1), all φn round to Lucas numbers, as we can see for the positive powers of φ above by comparing the coefficient in italic and the numerical value. As n increases, the difference quickly becomes extremely small. Multiplying (e) and (f), we obtain

φn Φn = (− 1)n = (Fn φ + Fn − 1)( − Fn φ + Fn + 1) = ( Fn √5 + Ln)( − Fn √5 + Ln) / 4,     (h)

from the third and fourth expressions, we obtain beautiful relations for the squares of the Fibonacci and Lucas numbers:

Fn2 = Fn − 1 Fn + 1 − (− 1)n,     Ln2 = 5 Fn2 + 4(− 1)n = 5 Fn − 1 Fn + 1 − (− 1)n.     (i)

The first equation is the famous Cassini identity, which was, however, already known to Kepler. If we multiply the two equations (g), or if we square them, we obtain respectively

F2n = Ln Fn     and     L2n = Ln2 − 2 (− 1)n = 5 Fn2 + 2 (− 1)n,     (j)

where the first equality of eq. (h) was used to derive the second set of equations. Equations (g), (i) and (j) are valid for all integer values of n.

***

Apart from the scalability, the reason why φ is important for polytopes has to do with the fact that it is the ratio of the length of the diagonal of the regular pentagon (L) to the length of its side (ℓ). The proof below is described in Livio (2002), but it is originally in Euclid's Elements. It decomposes the Pentagon into three isosceles triangles: one Golden triangle in the middle and two Golden gnomons on the sides.


Fig. 2.1a: The outside figure is a Pentagon, here built with B1 struts. This can be decomposed into a Golden triangle (at the centre) and two Golden gnomons on the left and right. The lines separating the inner Triangles (built here with B2 struts) are the diagonals of the Pentagon.


The larger angle of the Golden gnomon (β) is the inner angle at the vertex of the Pentagon, which as we'll see later is 108 degrees. Given that the two small sides of the Golden gnomon are identical (they are two consecutive sides of the Pentagon), its two remaining angles (γ) must also be identical. The sum of the inner angles of any triangle must be 180 degrees, so from β + γ + γ = 180, we obtain γ = 36 degrees. Since the Golden gnomon on the right also has angle γ at this vertex, the small angle of the Golden triangle is 108 − 36 − 36 = 36 degrees = γ; i.e., the diagonals of the Pentagon trisect its inner angle. Since the two identical angles of the Golden triangle (δ) plus γ must add up to 180 degrees, we obtain δ = 72 degrees.


Fig. 2.1b: Bisecting one of the C angles of the Golden Triangle, we obtain a Golden gnomon and a smaller Golden triangle, as shown below.


In Fig. 2.1b, we bisect one of the δ angles of the central Golden triangle, thus making two angles of 36 degrees = γ. This bisection divides the Golden triangle into two smaller triangles. For one of them, the smaller angles are both γ = 36 degrees, so it is a Golden gnomon.

The smaller triangle is very interesting: it has an angle given by γ, and from Fig. 2.1b we already knew that it has another angle given by δ, so the remaining angle must be 180 − 72 − 36 degrees = 72 degrees = δ. Thus the smaller triangle is another Golden triangle! Furthermore, since this and the previous Golden gnomon are isosceles triangles, and one of the equal sides is common, all their equal sides have length ℓ. To summarise, bisecting one of the larger angles of a Golden triangle, we decompose it into a Golden gnomon and a smaller Golden triangle.

The ratios between the larger and smaller sides of the large and small Golden triangles must be identical:

L / ℓ = ℓ / ℓ'

where ℓ' is the smaller side of the smaller Golden triangle. However, we see from Fig. 2.1b that L = ℓ + ℓ', thus,

(ℓ + ℓ') / ℓ = ℓ / ℓ',
1 + ℓ' / ℓ = ℓ / ℓ'.

If we replace ℓ / ℓ' by x we obtain eq. (a), which has the same numerical solution, φ. Thus φ is L / ℓ, the ratio of the diagonal of a Pentagon to its side, the ratio between the sides of the Golden triangle, the ratio of the sides of the Golden gnomon (hence their names) and the ratio of sizes between a Golden triangle and the smaller Golden triangle within it. This is, of course, the reason why we can represent Figs. 2.1a and b with B0, B1 and B2 struts. The full implications of this will become clear in Figs. 2.6a and b.

***

We now calculate the lengths of the other struts. For this, we will apply the Pythagorean theorem to estimate the lengths of the diagonals of a sequence of rectangles.

Before that, we note that their lengths are irrational numbers. The proof that the length of the diagonal of a Square or unit edge (√2) is irrational is very famous, having presumably been found by the Pythagoreans. However, this can be made much simpler and more general. If for an integer n √n were rational but not an integer, then it could be written as an irreducible fraction p/q, i.e., where p and q are integers with no common prime factors. However, this would imply that, after squaring this equality

n = p2/q2

the fraction on the right is also irreducible: it has the same set of prime factors on the numerator and denominator as p/q. Therefore n cannot be an integer, contradicting the assumption. n can only be an integer if q = 1, in which case it is a perfect square. The same argument is true for higher powers: apart from perfect cubes, all integers have irrational cubic roots, and so ad infinitum. This implies that φ is also irrational, because it is a sum of a rational and irrational number, √5.

Despite being irrational, the lengths of these diagonals are by definition constructible numbers because the diagonals can be constructed with a compass and straightedge in a finite number of steps. We will now show these constructions:


Fig. 2.2a: A Square built with B1 struts. Two HG1 struts represent the diagonal, they add to the length of a G1 strut.


Fig. 2.2b: A Rectangle built with B1 and G1 struts, the latter is the diagonal of the Square in Fig. 2.2a.


The Square in Fig. 2.2a has two B1 struts as sides, both with length 1. Thus, its diagonal is given by h = √ (1 + 1) = 1.414 213 562... This is the length of a G1 strut. The two HG1 struts shown have half this length, h/2 = √2 / 2 = 0.707 106 781... For other HG sizes, multiply by the different powers of φ.

The rectangle in Fig. 2.2b has B1 and G1 struts as sides, with lengths of 1 and √2. Thus, h = √ (1 + 2) = 1.733 050 807... The two Y1 struts shown have h/2 = √3 / 2 = 0.866 025 403... For other Y sizes, multiply by the different powers of φ. Because the diagonal is represented by yellow struts, I call this a Yellow rectangle. This has the proportions of A4 paper, which are kept when cut or folded in half withdways.

Mathematically, this process can go on forever, obtaining the lengths of all square roots, and building the Spiral of Theodorus. The next square root - of length 2 - is shown in Fig. 4.4a. In this page we continue instead with the Golden rectangle. In Figure 2.2c, we construct it from a Square with unit edge length (B1) on the left.


Fig. 2.2c: Construction of a Golden rectange from a Square.


We then mark the middle of the lower edge, open the compass to the upper right corner, covering a distance of √((1/2)2 + 1) = √5/2. Then mark that distance on the horizontal axis. The width of the full figure is now 1/2 + √5/2 = φ, in this case the length of a B2 strut. The length added to the side of the original Square is √5/2 − 1/2 = φ − 1 = 1/φ. From this, we see that one of the properties of Golden rectangles is that subtracting a Square (on the left), we obtain a smaller, vertical Golden rectangle (on the right). This property is analogous to the division of Golden triangles into Golden gnomons and smaller Golden triangles.


Fig. 2.2d: The diagonal of a Golden rectangle can be covered with two R1 struts.


Fig. 2.2e: A Rectangle built with B0 and B2 struts. Two Y1 sruts represent the diagonal.


The Golden rectangle in Fig. 2.2d has B1 and B2 struts as sides, with lengths of 1 and φ. Thus, h = √(1 + φ2) = √(2 + φ) = √ ((5 + √5) / 2) = 1.902 113 032... The two R1 struts shown have h/2 = √ ((5 + √5) / 8) = 0.951 056 516... For other R sizes, multiply by the different powers of φ.

Finally, the rectangle in Fig. 2.2e has B0 and B2 struts as sides, with lengths of 1/φ and φ. Thus:

h = √(φ2 + φ−2) = √L2 = √3     (k).

where we used the first (g) equation. The result is the same as in Fig. 2.2b, which means that the diagonal can also be covered by two Y1 struts, as we see in Fig. 2.2e! For this reason, I call this the Long yellow rectangle. Its area is given by φ × 1/φ = 1, i.e., the same as the Square in Fig. 2.2a. See model related to the Golden and Long yellow rectangles in Fig. 4.4b.

These lengths will be useful through the whole site, we will use them below to study the regular polygons. For many more models explaining the properties of the Zometool, see Hart (2000).

Zomable polygons

 There are many types of two-dimensional figures. In what follows, we will concentrate on polygons. We have already depicted a few polygons above (triangles, rectangles, the Square and the Pentagon): they are finite regions of 2-D Euclidean space* bound by at least 3 straight line segments, or sides; these sides meet in pairs, in angles different from 0 and 180 degrees, at an identical number of vertices. In what follows, we regard all polygons and generally polytopes as closed sets, which means that their surface elements (henceforth "elements") are also part of them.

* This is the traditional definition of a polygon. We will not consider here apeirogons, skew polygons, or complex polygons.

A regular polygon (henceforth Polygons) is isogonal and isotoxal. This means that not only are the elements identical (sides of the same length, edge-vertex-edge angles - the "inner angles" - identical), but the polygon looks the same from all elements of a particular type. It follows from this that the polygon has a well defined centre and that all elements of a particular type are equidistant from it.

The names of polygons generally denote the number of sides, which is the the same as the number of vertices; for instance the name ``pentagon'' means ``five sides'' in Greek. In this site we use capitalised polygon names to refer to their regular forms. The non-Greek names are the triangle, which refers to the three inner angles, and the quadrilaterals: Isogonal quadrilaterals are called rectangles, isotoxal quadrilaterals are called rhombuses; isogonal and isotoxal are regular, the Square.

The polygons shown above can be built with the Zometool, i.e., they are Zomable. We now expand this, depicting other Zomable Polygons and special rhombuses. Because the Zometool parts represent only points (with the balls) and line segments (with the struts), it only represents the surface elements of the polygons, the vertices and the sides. We also display a strut connecting the vertex of the polygon to its center if this can be represented with the Zometool, which tells us something about its metric properties. This study will be useful for the latter study of figures in higher dimensions, also for showcasing the capabilities of the Zometool system.

All Zomable polygons depicted in this page, including all regular polygons, are constructible, i.e., they can be built with a compass and straightedge. However, this is not the case for most polygons.


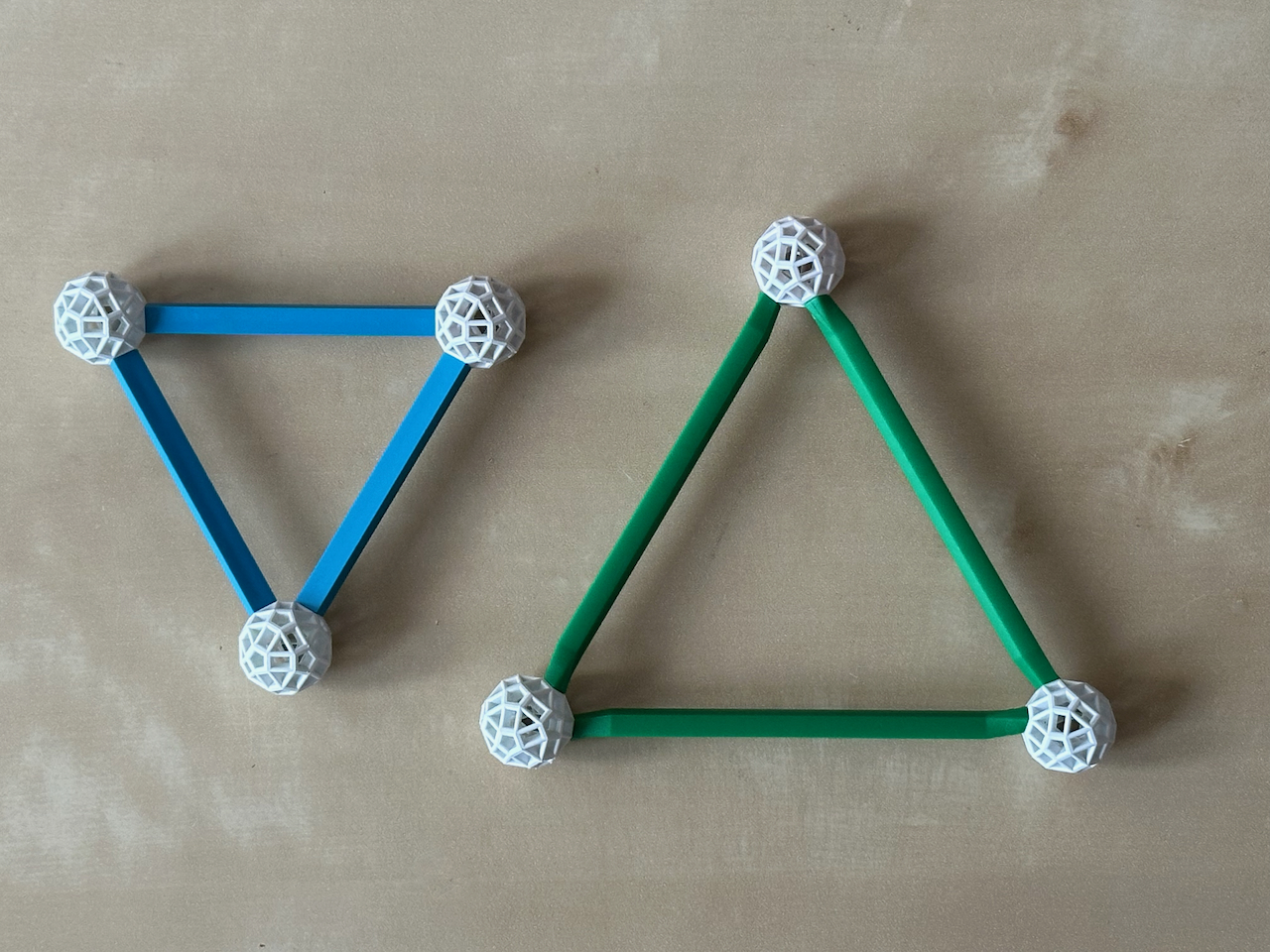
Fig. 2.3a: Triangles can be huilt with B and G struts.


Fig. 2.3b: Squares, which we have already seen built with B struts (fig. 2.2a), can also be built with G struts. Additionally, we can also see that the distance from the centre of the square to a vertex can be represented by struts of the other colour.


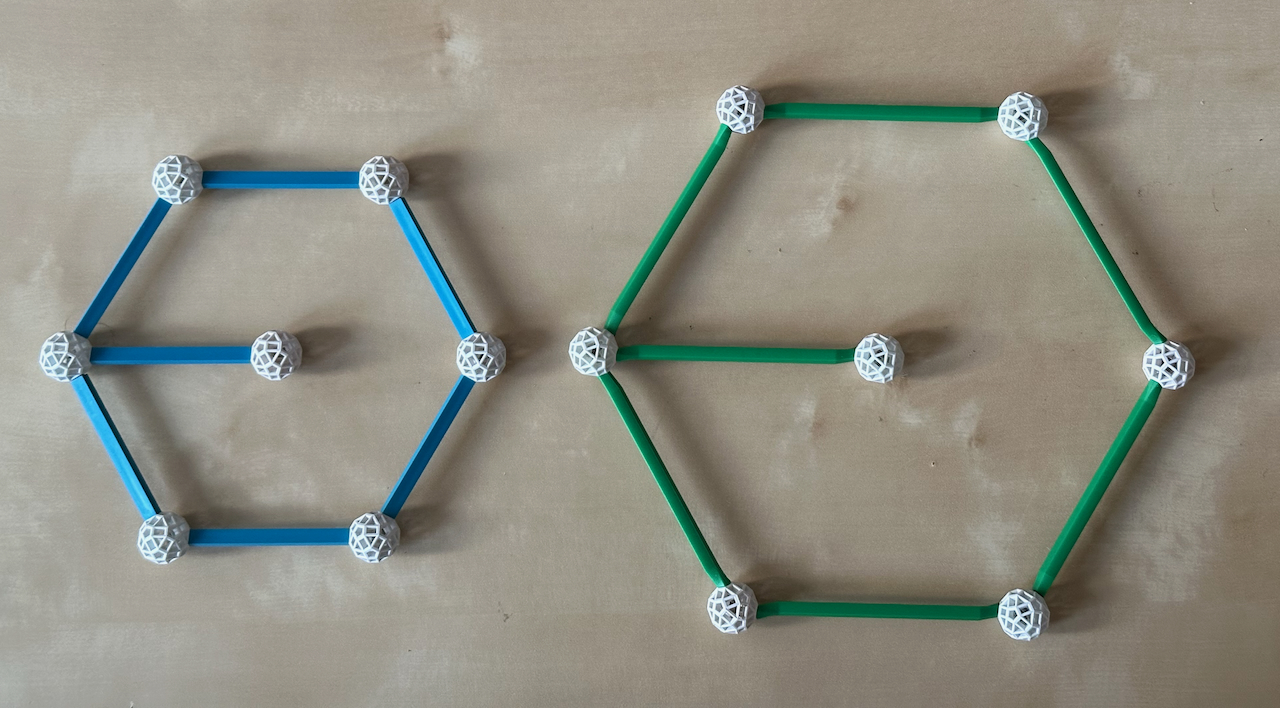
Fig. 2.3c: Hexagons can be built with B and G struts; this is a consequence of this also being true for Triangles, six of which can fill the Hexagon.


In Fig. 2.3c, the distance from the centre of the Hexagon to a vertex can be represented by struts of the same colour and length as its edges. This means that the distance of the centre to the vertex is the same as its side, i.e., the Hexagon is radially equilateral. It is the only Polygon with this characteristic.

Heptagons, Octagons and Nonagons are not Zomable. The Heptagon and Nonagon are non-constructible, the simplest such figures. The Octagon is easily constructible, but the fact that it is not Zomable will have important implications later. However, there is one last Zomable convex Polygon, the Decagon; which like the Pentagon (Figs. 2.1a, b) can only be built with B struts.


Fig. 2.3d: Like the Pentagon, the Decagon can only be built with B struts.


In Fig. 2.3d, since the angle subtended by each side at the centre is 360 / 10 = 36 degrees, we can decompose the Decagon into ten Golden triangles radiating from the centre (one of them represented in the figure). Thus, the distance from the centre to a vertex is the same as the diagonal of a Pentagon of the same side (Figs. 2.1a, b), φ times longer than the sides, and thus representable with a 1 size larger B strut.


Fig. 2.3e: The ditrigonal hexagons. These three hexagons share the same vertex arrangement, all of them are isogonal, but have edges with two lengths.


Of course, with Zometool we can represent many irregular polygons. In Fig. 2.3e, I show three special cases of irregular hexagons with 3-fold symmetry, the ditrigonal hexagons: these are, on top, the ditrigon, on lower left the propeller tripod and on lower right the tripod. The three share the same vertex arrangement and are all isogonal (within each polygon, they have the same angle and side lengths at each vertex: 120 degrees for the ditrigon, 60 degrees for the tripods), but their edges come in two different lengths, i.e., they are not isotoxal. The lengths of the edges are: 1 and 1/φ for the ditrigon, φ and 1/φ for the propeller tripod and φ and 1 for the tripod. The tripods are non-convex; furthermore, their long edges cross each other (each one crosses the other two). This makes them star polygons. These crossing points are false vertices (represented by the inner balls), because no edge ends there.

Geometric relations

To continue, we will now discuss several geometric transformations between polygons, which will be useful to understand all polytopes in general, they will also give us an opportunity to discuss regular star polygons and several special non-regular quadrilaterals.

Duality: If polygons A and B are dual, then to a vertex of A corresponds an edge of B. This is a reciprocal relation, so to each vertex of B corresponds an edge of A. Two dual polygons have the same symmetry.

We now show examples of the rectangle-rhombus duality: To the isogonal Rectangles correspond the isotoxal rhombuses; to the alternate side lengths of the rectangles correspond the alternate angles of the rhombuses. The rhombuses touch the rectangles at right angles with a line from the vertex of the rectangle to the centre; this is known as the `` Dorman Luke'' construction, which can be used in any case where a polygon has a centre. In the figues below, we demonstrate this by drawing a special circle, which touches all the vertices of the rectangles (i.e, this circle circumscribes the rectangles) and tangentially touches all the sides of the rhombuses (i.e., this circle is inscribed in the rhombuses).


Fig. 2.4a: The Yellow rectangle and its dual, the Yellow rhombus. To achieve this particular construction, we had to glue two yellow rectangles by their longer sides, obtaining a larger Yellow rectangle.


Fig. 2.4b: The Golden rectangle and its dual, the Golden rhombus.


Fig. 2.4c: The Long yellow rectangle and its dual, the Long yellow rhombus.


Thus, the duals of the Yellow, Golden and Long Yellow rectangles in Figs. 2.2b, d and e are the Yellow, Golden and Long yellow rhombuses in Figs. 2.4a, b and c.

The dual of the isogonal ditrigonal hexagons in Fig. 2.3e is a set of isotoxal hexagons, also possessing 3-fold symmetry, the triambuses. These are, however, not Zomable.

If a polygon is regular, its dual is of the same kind, but rotated by 180 deg / n, where n is the number of sides of the Polygons (see Fig. 2.4d). Thus, unlike most other types of polygons, regular polygons are self-dual.


Fig. 2.4d: The dual of a regular Polygon like the Pentagon is of the same kind: another Pentagon. The inner and outer Pentagons are duals of each other.


Rectification: Rectification consists of marking the mid-points of the sides of a polygon and cutting off the vertices at those points. This results in a new polygon, which is the rectification of the first one.

In the case of a Polygon, the rectification is of the same kind, but rotated by 180 deg / n, where n is the number of sides of the Polygons, and smaller. In Fig. 2.4d, the inner Pentagon, which is the dual of the outer pentagon, is also its rectification.

However, the rectification is not the same as a duality. If we rectify Yellow, Golden or Long yellow rhombuses, we obtain again Yellow, Golden or Long yellow rectangles, but in an orthogonal direction to that in Figs. 2.4a, b and c. In the next Figures, we see that the Rhombic diagonals are in the same proportions as the sides of the resulting rectangles, but twice as long, as shown later in Fig. 4.9. Thus, all struts of the rectangles in Figs. 2.5a, b and c are necessary to trace the diagonals of their respective rhombuses.


Fig. 2.5a: The rectification of a yellow rhombus is a Yellow rectangle.


Fig. 2.5b: The rectification of a Golden rhombus is a Golden rectangle.


Fig. 2.5c: The rectification of a Long yellow rhombus is a Long yellow rectangle.


Note that the sides of the rhombuses are as long as the diagonals of the rectangles. Also, it should be clear that the rectifications of these Rectangles results again in the original rhombuses, but with half the size.

The rectifications of Figs. 2.5a, b and c are special cases of rectifications of quadrilaterals, which by Varignon's theorem are always parallelograms.

Stellation and faceting: A stellation extends the edges of a polygon until they meet other similarly extended edges of the same polygon. Stellations can transform a Polygon into a larger star polygon. The simplest case is that of the Pentagon (if we stellate Triangles and Squares, their edges would never meet), which stellates into a Pentagram (see Figure).

Facetings cut into a polygon, but preserve its vertices. Like the stellations, they cannot be convex. In Fig. 2.3e, we saw two examples of faceting: the two tripods are facetings of the ditrigon. In what follows we show additional examples of facetings.


Fig. 2.6a: By extending the edges of the inner Pentagon, with vertices in white and dark blue B1 struts, the stellation operation results in a Pentagram, with vertices in black.


Fig. 2.6b: The Pentagram can be inscribed in a larger Pentagon, also with black vertices and B3 struts, i.e., φ2 larger than the side of the inner Pentagon. In this Figure, there are 15 Golden Gnomons and 20 Golden triangles.


In Fig. 2.6a, the inner white vertices are false vertices of the Pentagram. The new Triangular areas that were added with the stellation of the Pentagon are Golden triangles; with the two larger sides being equal to the diagonal of the Pentagon, φ times its side (Figs. 2.1a, b). Thus, the side of the Pentagram is 1 + 2 φ = φ3 the side of the inner Pentagon.

In Fig. 2.6b, we inscribe the Pentagram in a larger Pentagon, which as can see, is the dual of the inner Pentagon (see Fig. 2.4d). Because the real vertices are the same (in black), the Pentagram is a faceting of the outer Pentagon. The sides of the Pentagram are the full set of diagonals of the outer Pentagon. Since the diagonals are φ times larger then the side of the outer Pentagon (see Figs. 2.1a, b), that side is only φ2 larger than the side of the inner Pentagon. We see how these diagonals divide the whole surface of the outer Pentagon into Golden triangles, gnomons and a smaller Pentagon. This can be done again for the inner Pentagon, again and again ad infinitum.

In the next figure, we stellate a Hexagon. This results is a regular compound of two Triangles with sides three times larger, the Hexagram. This is the simplest of the regular polygon compounds, the polygrams. This Hexagram can be inscribed in a larger dual Hexagon, which it facets. As we've seen in Fig. 2.3e, there are star hexagons, but none of them is regular.


Fig. 2.7: The stellation transforms the inner Hexagon, with vertices in white and light green G1 struts, into a regular polygon compound, the Hexagram, with vertices in black. The inner white vertices are false vertices of the Hexagram.


The larger the number of sides/vertices of a polygon, the larger the number of distinct stellations and facetings. This is, as we'll see now, the case of the Decagon, for which we show all three distinct stellations. The first is a Polygram, consisting of two Pentagons. The second is a regular star polygon, the Decagram. The third is another Polygram, a compound of two Pentagrams. All of these are also facetings of of the Decagon.


Fig. 2.8a: The first stellation of the Decagon (here in dark blue B1 struts and white vertices) is a compound of two Pentagons, here with yellow vertices. The white vertices further in are now false vertices.


2.8b: The second stellation of the Decagon is the Decagram, here with black vertices. The white and yellow vertices further in are now false vertices.


Fig. 2.8c: The Decagram can be inscribed in a Decagon, which has edges built with B2 struts.

Notice how the radial struts bissect the quadrilaterals into Golden triangles, they also define central Golden triangles. Notice too the three sizes of Golden gnomons.


Fig. 2.8d: The third and last stellation of the Decagon is a compound of two Pentagrams, here with red vertices. These also result from stellating the two Pentagons with yellow vertices. The white, yellow and black vertices further in are now false vertices. Figures 2.8c and d show how many times φ appears in these geometric objects.


In Fig. 2.8b, the side of the Decagram is represented by three B1 and two B0 struts, which means it has a length 3 + 2 / φ = 1 + 2 φ = φ3 larger than the side of the inner Decagon, represented by B1 struts. Importantly, this is the same proportion as for the Pentagram and Pentagon.

In Fig. 2.8c, we inscribe this Decagram within a large Decagon. Since the real vertices are the same (in black), this means that the Decagram is a faceting of the outer Decagon. The latter is φ times larger but has, importantly, the same orientation of the inner Decagon. The distance of a vertex to the center, which was φ, now becomes φ + 1 = φ2.

Isomorphism: The Pentagon and Pentagram are isomorphic: they have same number of sides and vertices with the same topology (a single circuit going through five vertices and sides). They have the same configuration matrix. The same happens for the Decagon and Decagram. However, the Hexagon and the Hexagram are not isomorphic, since in the latter case there is not a single circuit that cover all vertices, but two (the two Triangles of the compound) - the two figures have different topologies.

Metric properties and symmetry

 In this page, I will not dwell much on the mathematical aspects of polytopes; the references cover that very well. However, a few of the metric properties of polygons keep reappearing and being useful for understanding the polytopes in this page. For this reason I will discuss them here. I will however, make a couple general remarks about their symmetries first.

Some polygons have central symmetry: each element is reflected through the centre of the polygon into an identical one. In such polygons not only must the number of sides / vertices be even (as for instance, in the aforementioned rectangles and rhombuses), but also the symmetry of the figure must be even. As an example, the ditrigons and tripods in Fig. 2.3e (and their duals, the triambuses) have an even number of sides (6), but because their overall symmetry is Triangular (order 3), they have no central symmetry. This will be important for understanding rectified and partially regular polytopes.

The regular polygons are much more symmetric, having dihedral symmetry. If their number of sides / vertices is even, then they automatically have central symmetry, which is in that case a sub-symmetry within the dihedral symmetry. Thus, if a Polygon has central symmetry, its number of vertices/sides must be even.

The idea of a polygon as a circuit mentioned above will be discussed in more detail now. As we go around a polygon, we pass through n vertices, while completing p turns around the centre. For convex Polygons, p =1, but for the Pentagram, we actually complete two turns around the centre, and for a Decagram 3 turns. This number is known as the polygon's density.

If there are common factors in n and p, we are in the presence of a Polygram. For instance, in Fig. 2.7, n = 6 and p = 2, hence two is a common factor, and thus we have 2 independent circuits (Polygons), each with n / p = 3 sides. Equally, for Fig. 2.8a, n = 10 and p = 2; 2 is the common factor and because of this we have 2 Polygons, each with n / p = 5 sides. Finally, in Fig. 2.8d, n = 10 and p = 4, 2 is a common factor, so we have 2 Polygons, each with n = 5 and p = 2, i.e., two Pentagrams.

The angle subtended by two vertices as seen from the centre must add to 360 degrees × p:

α = 360 p / n,

This angle is also the change of direction at each vertex, as we move from one side to the next. Thus, the inner angle at the vertex is the supplementary angle:

β = 180 − 360 p/n.

These angles are listed in Table 1 below, for instance, for a Triangle, the inner angles are 60 degrees. The sum is therefore 180 degrees. This sum is valid for all triangles in flat, Euclidean spaces. For the Pentagon, we obtain the aforementioned inner angle of 108 degrees.




Fig. 2.9: Definition of the main angles of a Polygon. The black circle circunscribes the Polygon, and has radius R0, the side is given by ℓ.


Now, if the vertices are at distance R0 from the centre (see Fig. 2.9), the sides (with length ℓ) are the chord of α times R0:

ℓ = R0 chord(α)

Replacing the sine expression of the chord and solving for R0, we obtain (see also Fig. 2.9):

R0 = ℓ / (2 sin (α / 2)) = ℓ / ( 2 sin (180 p / n))

The minimum distance of the side to the centre is given by:

R1 = √ (R02 − (ℓ / 2)2) = ℓ / (2 tan (α / 2)) = ℓ / (2 tan (180 p / n))

The surface of the Polygon is the same as that of 2 n triangles with base ℓ/2 and height R1.

Another important quantity is chord(β). This is, for any particular vertex P, the distance between the two vertices it connects to divided by their distance from P (ℓ). In Fig. 2.1a, the diagonal of the Pentagon has length L = chord(β) ℓ; L is the side of the inscribed Pentagram (Fig. 2.6b). Generally chord(β) ℓ is the side of the first faceting of a convex Polygon of side ℓ.

A consequence of the Zomable Polygons being constructible is that the sines in the equations for R0, R1 and chord(β) are a subset of the constructible numbers, the exact trigonometric values. From these, we obtain the values listed below:

Polygon α β R0/ℓ R1/ℓ chord(β)
Triangle 120 60 1 / √3 1 / (2 √3) 1
Square 90 90 √2 / 2 1 / 2 √2
Hexagon 60 120 1 √3 / 2 √3
Pentagon 72 108 √( (5 + √5) / 10) 1 / (2 √(5 − 2 √5)) (√5 + 1) / 2
Decagon 36 144 (√5 + 1) / 2 √(5 + 2 √5) / 2 √((5 + √5) / 2)
Pentagram 144 36 √2 / √(5 + √5) 1 / (2 √(5 + 2 √5) ) (√5 − 1) / 2
Decagram 108 72 (√5 − 1) / 2 √5 / (2 √(5 + 2 √5)) √2 √(5 − √5) / 2
Table 1: Metric properties of Zomable Polygons

Some R0 lengths and chords are indicated in boldface because they are Zomable: Regarding the Decagram, These properties will be important for a few polytopes to be mentioned later!


Paulo's polytope site / Next: Polyhedra