Making Maps

The gridding algorithms that are usually used to make maps of spectral line data employ a simple triangulation scheme. This method works well if the data is sampled on a regular grid like the one that PRASTER produces. However, if the data points are distributed irregularly (like when OTF mapping), the triangulation introduces strong artifacts which make the maps useless. Instead, more advanced schemes like ``Gauss $\times$ Sinc'' weighting or ``Orthogonal Convolution'' algorithms should be used.

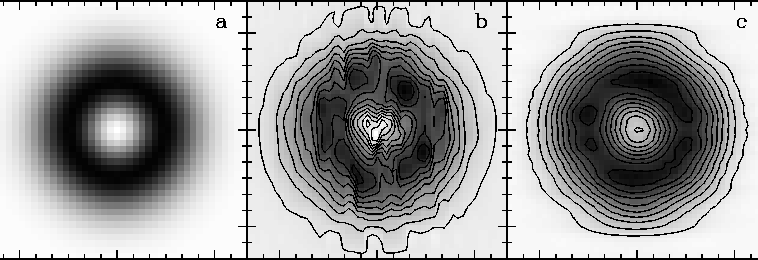
To demonstrate this effect, we have set up a ring shaped test source, added some noise and sampled it on a rectangular grid with some positional jitter (like it occurs in OTF due to variations in the startup time to accelerate the telescope to the scanning speed). We then fed the data into the triangulation command used in the Grenoble Software (GREG2 $\backslash$RANDOM_MAP) and into the Orthogonal Convolution scheme used by the latest Unix version (10/1998) of Robert Zylka's MOPSI (MAP $\backslash$RANDOM).

Figure 2 shows the results of this test. The triangulation (panel b) introduces strong striping artefacts because of the positional jitter and the noise while the Orthogonal Convolution map shows a result close to the expected structure. We strongly recommend to use such an algorithm to grid the OTF data. CLASS has a built-in gridding command called GRID. We have also have MOPSI and there are the gridding tasks GRID_EXTEND and GRID_SG in GRAPHIC. MOPSI is much faster than the other methods, but we recently discovered a problem with shift in the the velocity axis when writing the data from MOPSI to Gildas Data Format (GDF). This bug has NOT yet been fixed ! We therefore recommend using CLASS' GRID to reduce spectral line OTF data.

  

Figure 2: Gridding simulated OTF observations of a ring shaped test source (panel a) with the triangulation method (e.g. GREG's RANDOM_MAP, panel b) and with an orthogonal convolution algorithm (e.g. MOPSI, panel c). The triangulation scheme introduces strong artefacts for the OTF data due to the non-square sampling, the noise and the position jitter. The orthogonal convolution algorithm handles the OTF data much better and produces a result close to the original source. It is therefore the preferred OTF gridding algorithm.