 |  |  |  |
 |  |  |  |
This simulation investigates the influence of the FFTS performance on the quality of the reconstructions. This means that the AO will give a strehl of 0.30 and the FFTS will give a residual OPD error.
The setup of the simulation is described in table 1. The input data for the test uses a strehl value of 0.30 for the target and the calibrator which has a magnitude of 14. In addition the target and calibrator images are influenced by a gaussian distributed phase error with the same standard deviation, resulting in a fringe contrast loss. This error is modelled as a phase error on the second pupil and for each phase screen (the properties of the atmosphere will result in about 600 phase screens per position angle) a random phase error is introduced. This phase error is specified as a gaussian error with a standard deviation of the OPD between 0.0 (perfect FFTS) and 0.5 lambda (worst case, no FFTS available).
| Parameter | Description |
|---|---|
| Atmosphere/AO | The AO delivers a strehl of about 30 percent for the target and the psf star. The psfs are separately simulated and therefore not equal! |
| FFTS | The FFTS will leave a residual phase error which is given as a standard deviation of 0.0, 0.05, 0.1, 0.2, and 0.5 lambda. |
| Observation | The observation target is NGC4151 with an overlayed dust tori (simulated) at 10.1mag integral brightness. The brightness of the calibrator is set to 14mag. For each position angle (108, 144, 180, 216, 252 degree) an image equivalent to 60s exposure time was created. The wavelength was 1.2 micron (whole J-Band) and 2.2 micron (whole K-band). |
The raw data were generated according to the common scheme described in section Overview. In addition the phase screens for the psfs are influenced by a phase error on the second pupil, and the images for the target and psf-star are generated separately which means, that the calibrator image is not influenced by the target (no halo, etc.).
All simulated input data for the LN DRS pipeline are available as a tar-file (ex3_j_input.tar.gz (18MB) and ex3_k_input.tar.gz (20MB)). The corresponding results are also available as tar files (ex3_j_results.tar.gz (2.7MB) and ex3_k_results.tar.gz (2.8MB)).
The generated calibrator raw images are shown in section Calibrator. The raw images and deconvolution results are shown in section Raw Frames and Results for an AGN for the AGN and section Raw Frames and Results for a Star Cluster for the star cluster.
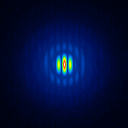
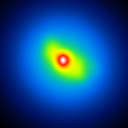
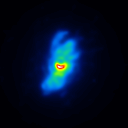
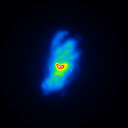
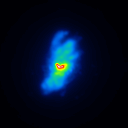
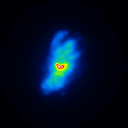
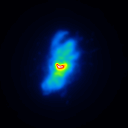
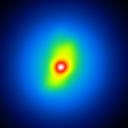
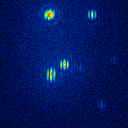
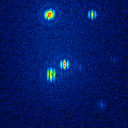
The simulated raw LBT interferograms used for the deconvolution are ideal images, they are not influenced by detector effects like different pixel gain or bad pixels. In figure 1 the calibrators for the different phase errors and one position angle are shown.
 |  |  |  |
 |  |  |  |
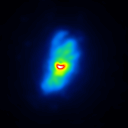
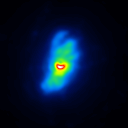
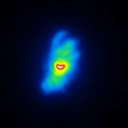
The basis of the simulation is an image of NGC4151 with an overlayed dust torus (see figure 1). The simulated raw images for a position angle of 108 degree are shown in figure 2.
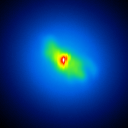 | 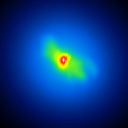 | 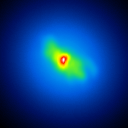 | 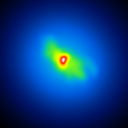 |
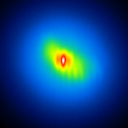 | 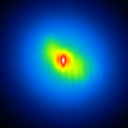 | 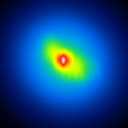 |  |
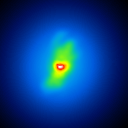
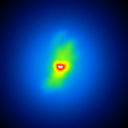
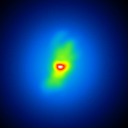
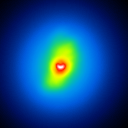
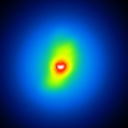
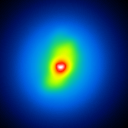
A comparison of the reconstructions depending on the phase error is presented in figure 3 for the J-Band. For the K-Band the results are presented in figure 4.
 |  |  | 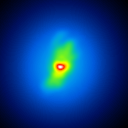 |
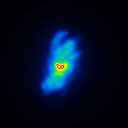 | 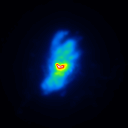 | 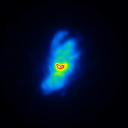 |  |
 |  |  |  |
 |  |  |  |
 |  |  | 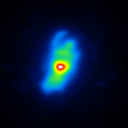 |
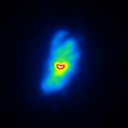 | 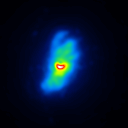 | 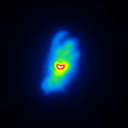 |  |
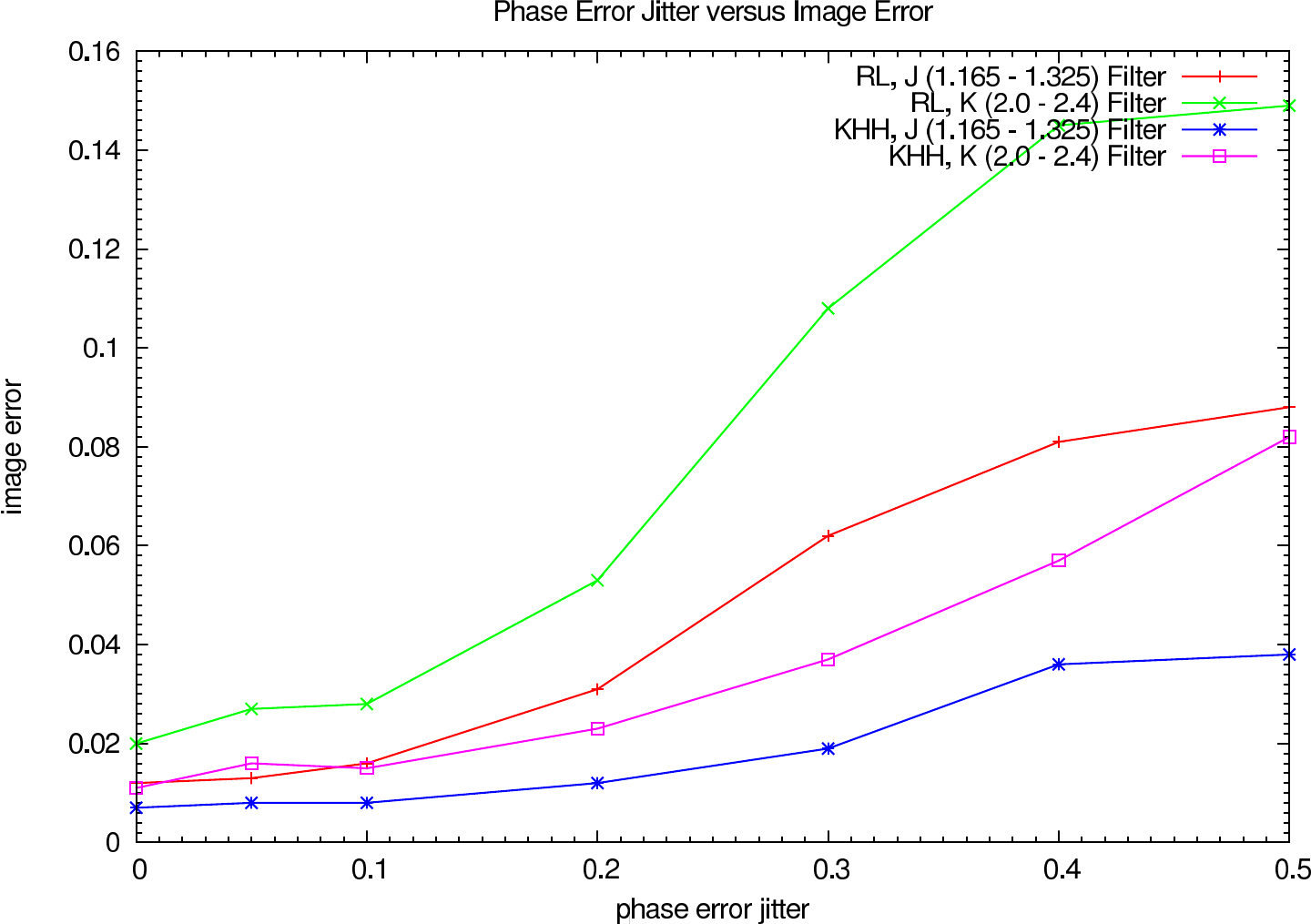
In table 2 (J-Band) and table 3 (K-Band) the errors for the star cluster depending on the OPD error are presented. In figure 5 the image errors depending on the phase error jitter are shown.
| Testcase | Richardson-Lucy | Building-Block |
|---|---|---|
| Phase Error | Image Error | Image Error |
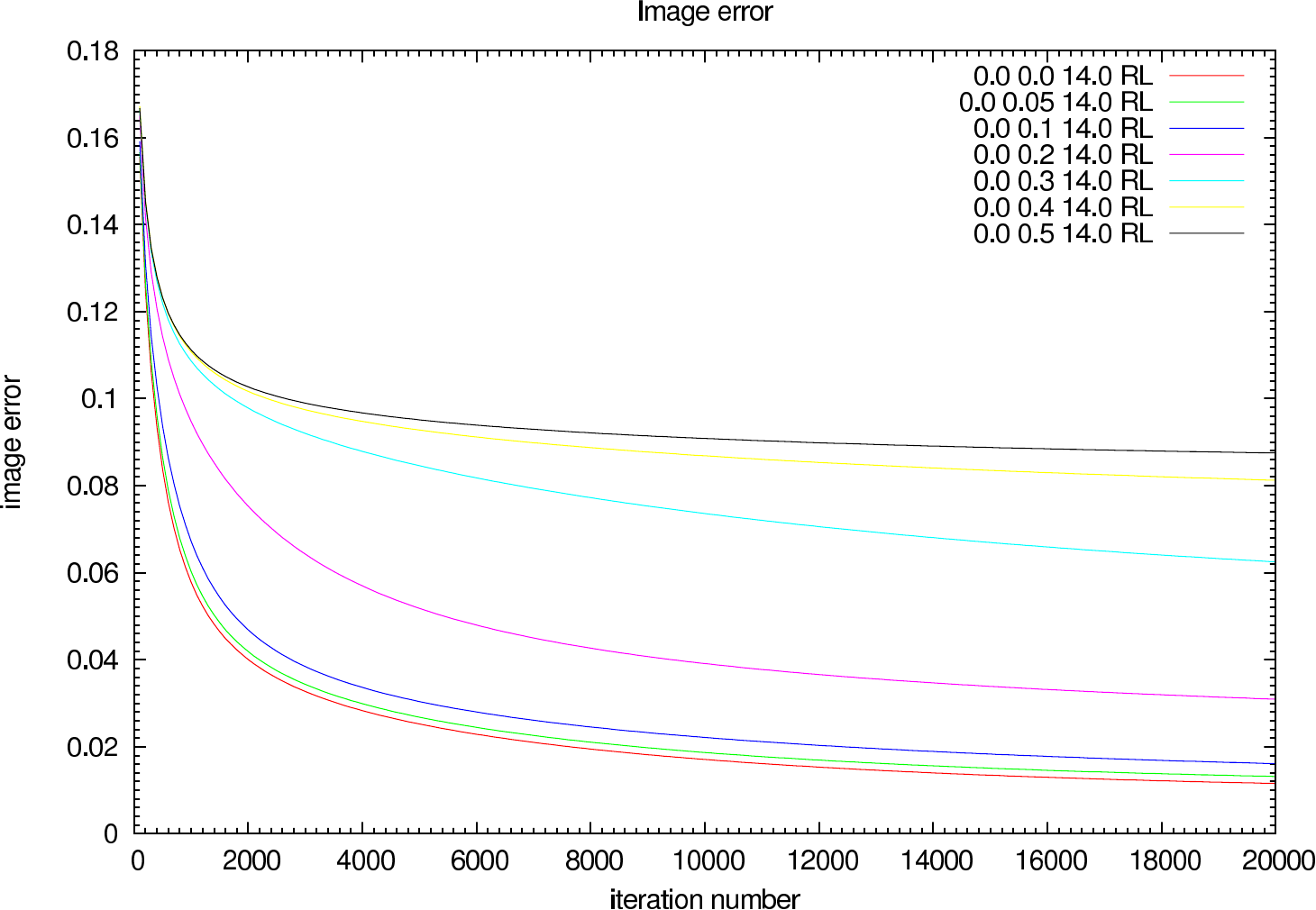
| 0.0 0.0 | 0.012 (0.012) | 0.007 (0.007) |
| 0.0 0.05 | 0.013 (0.013) | 0.008 (0.008) |
| 0.0 0.1 | 0.016 (0.016) | 0.008 (0.008) |
| 0.0 0.2 | 0.031 (0.031) | 0.012 (0.012) |
| 0.0 0.3 | 0.062 (0.062) | 0.019 (0.019) |
| 0.0 0.4 | 0.081 (0.081) | 0.036 (0.036) |
| 0.0 0.5 | 0.088 (0.088) | 0.038 (0.038) |
| Testcase | Richardson-Lucy | Building-Block |
|---|---|---|
| Phase Error | Image Error | Image Error |
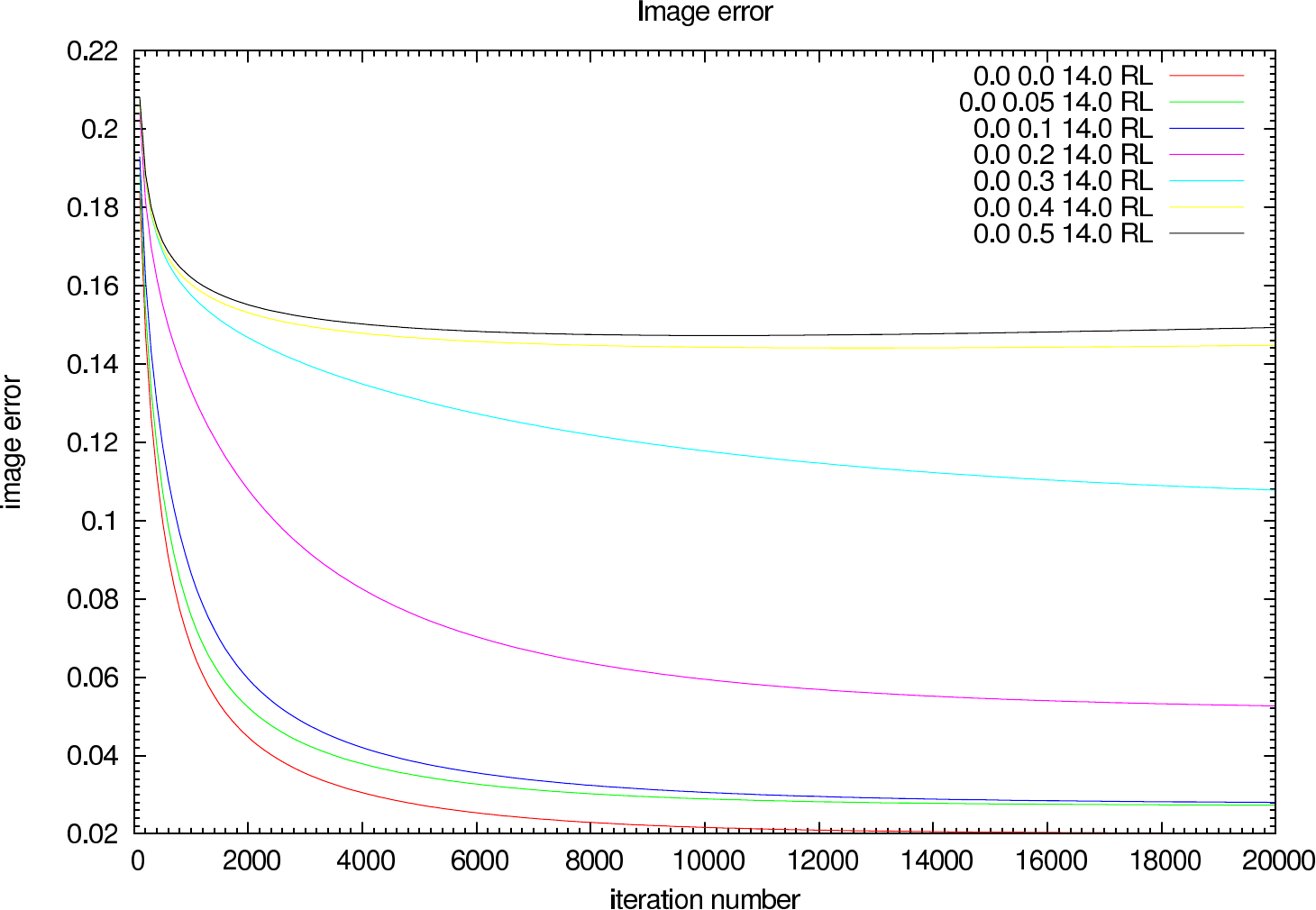
| 0.0 0.0 | 0.020 (0.020) | 0.011 (0.011) |
| 0.0 0.05 | 0.027 (0.027) | 0.016 (0.016) |
| 0.0 0.1 | 0.028 (0.028) | 0.014 (0.014) |
| 0.0 0.2 | 0.053 (0.053) | 0.022 (0.022) |
| 0.0 0.3 | 0.108 (0.108) | 0.035 (0.035) |
| 0.0 0.4 | 0.145 (0.144) | 0.057 (0.057) |
| 0.0 0.5 | 0.149 (0.147) | 0.082 (0.082) |
 |
In figure 6 the image error describing the difference between the reconstruction and the reference image is shown for each iteration (in steps of 100 iterations). The effect of the OPD error on the reconstruction error and the optimal iteration number is clearly visible.
 |  |
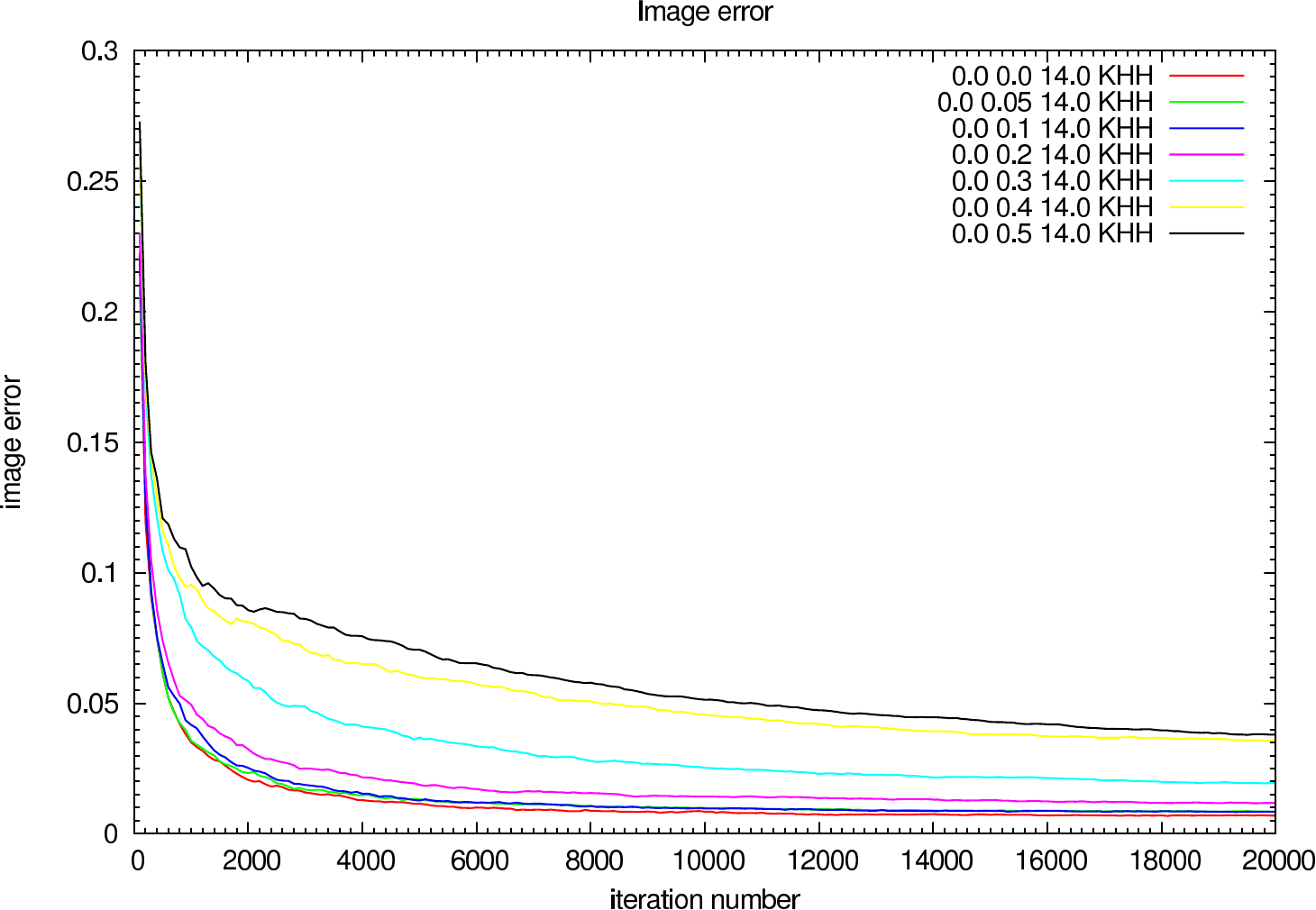 | 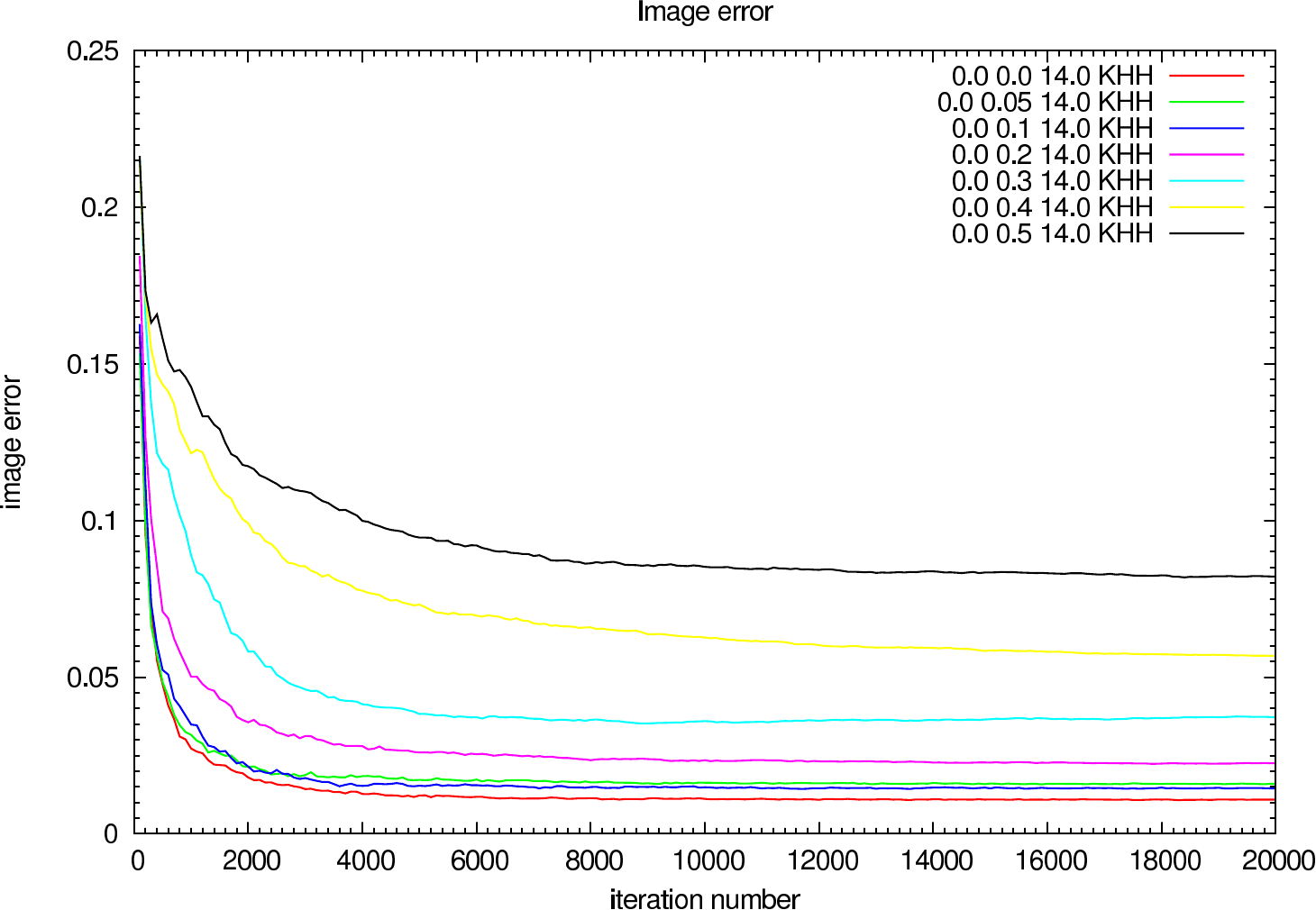 |
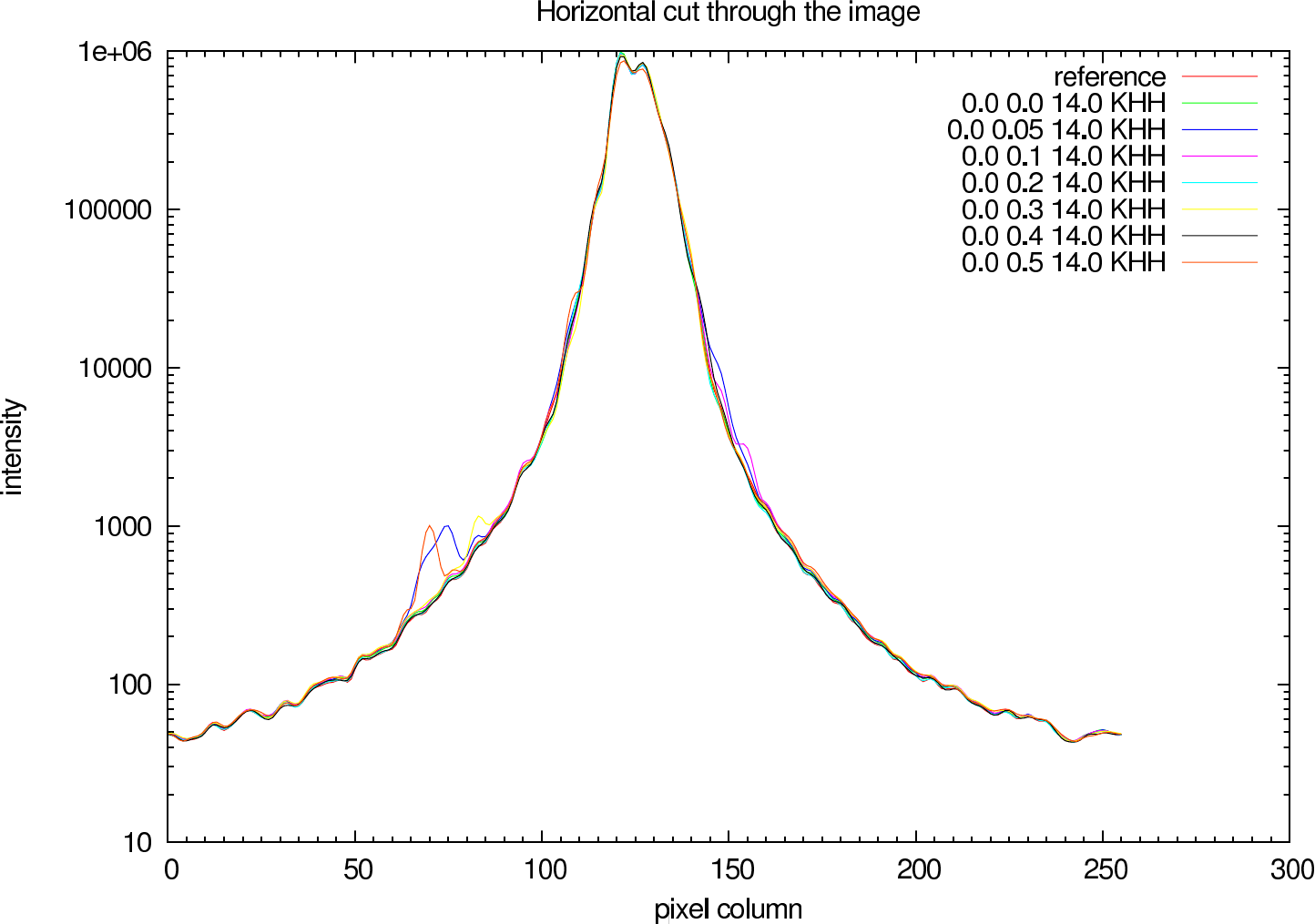
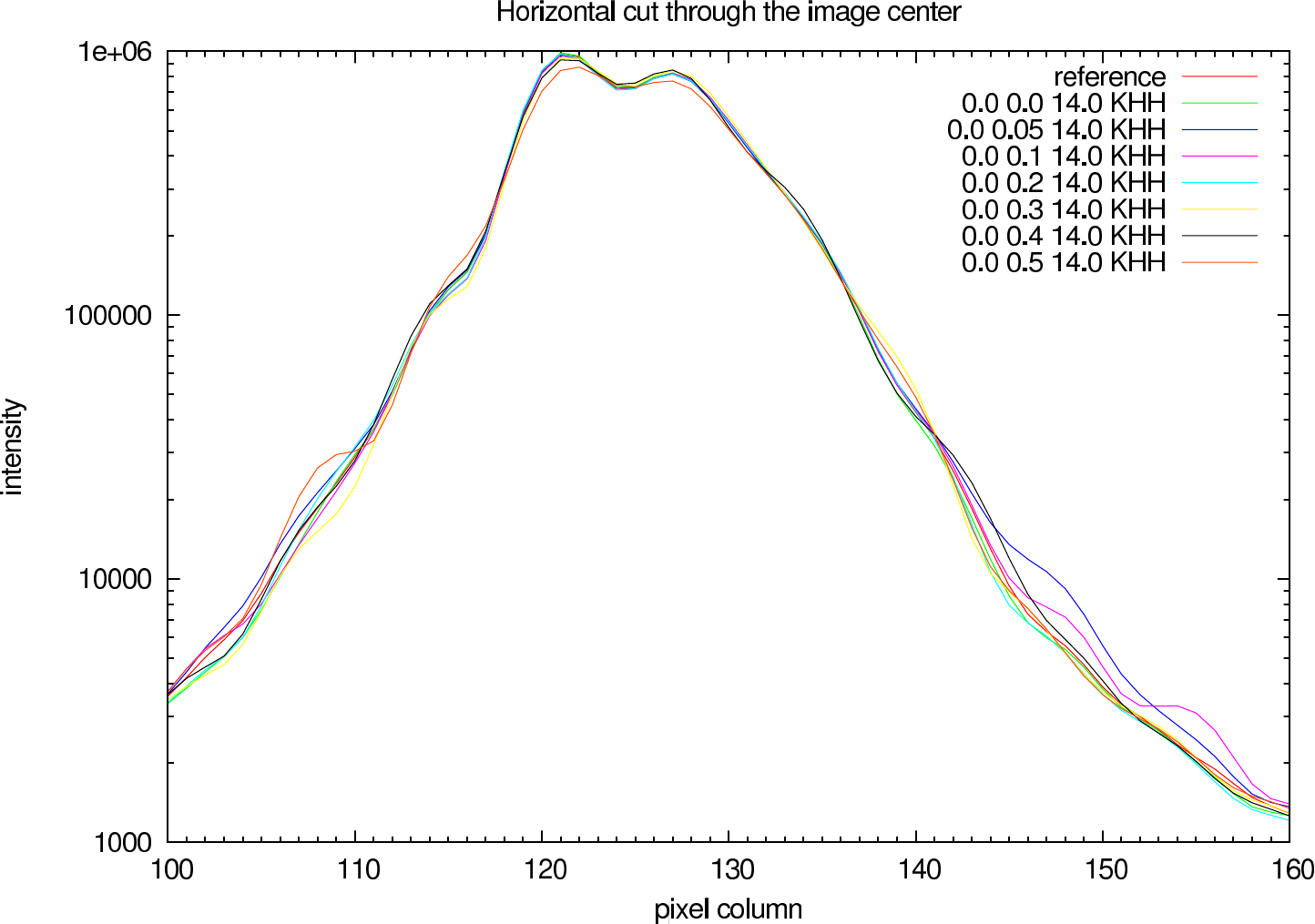
In figure 7 (J-Band) and figure 8 (K-Band) a horizontal cut slightly above the intensity maximum of the reconstructions of NHC4151 compared with the ideal reference image is shown.
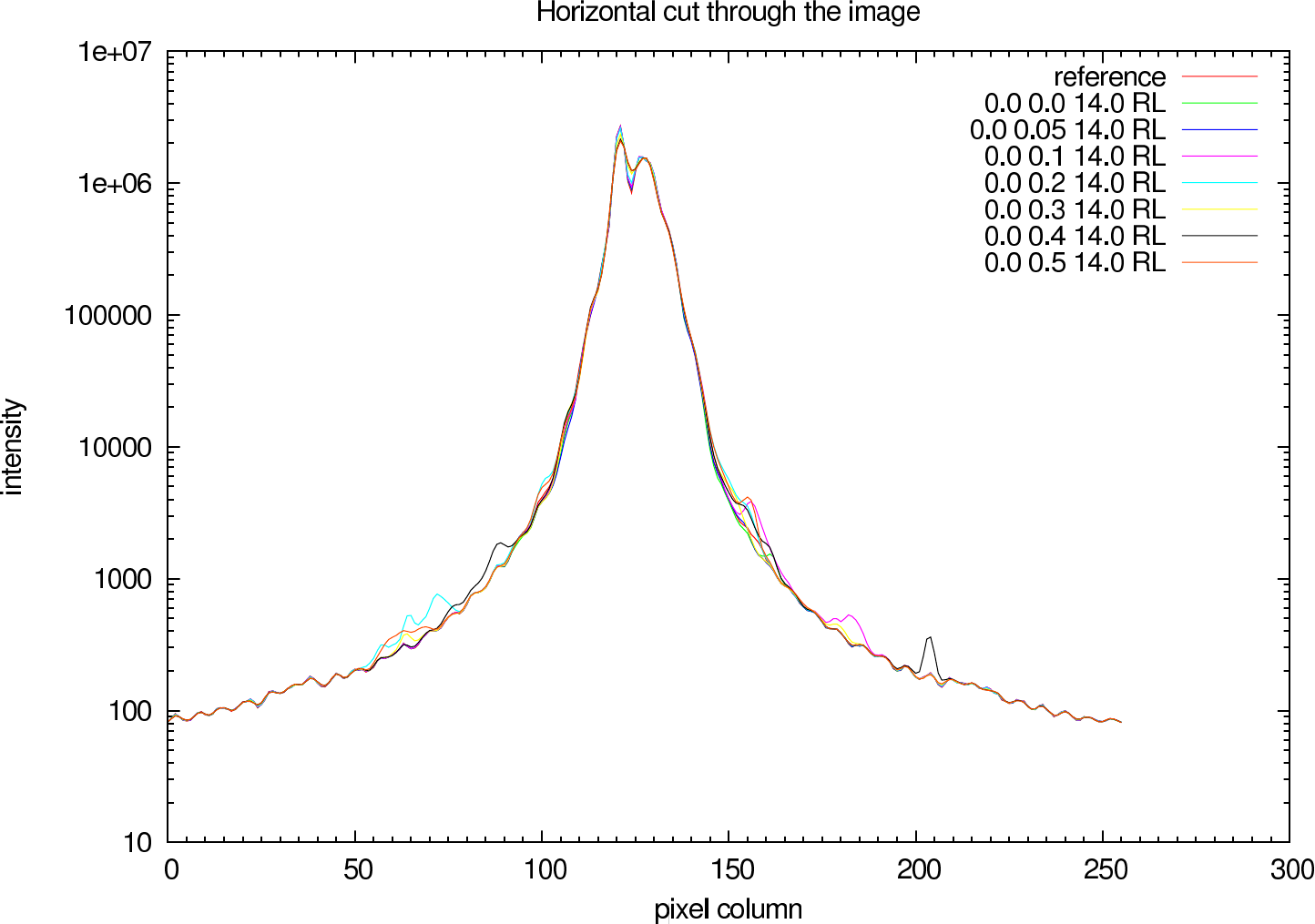 | 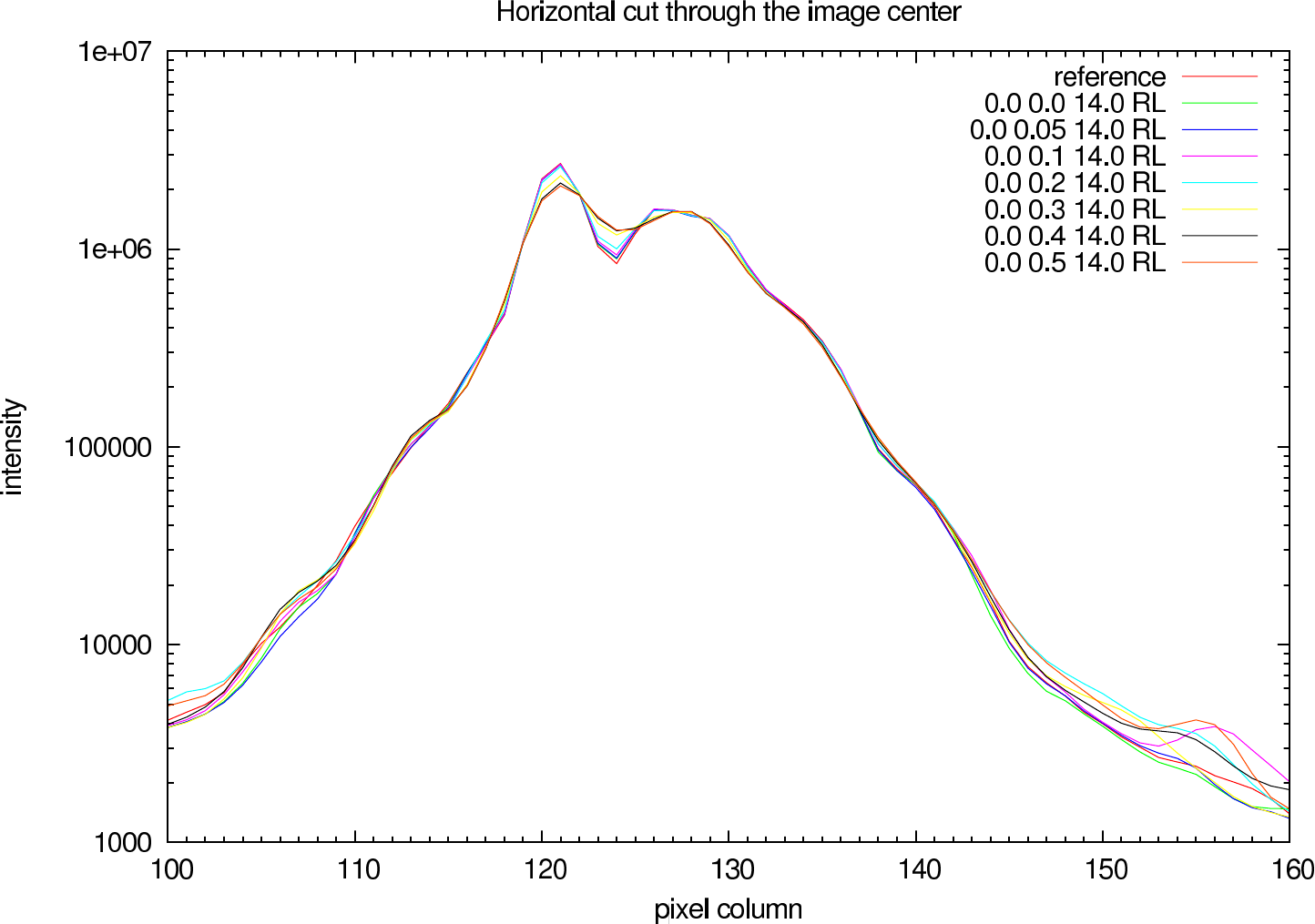 |
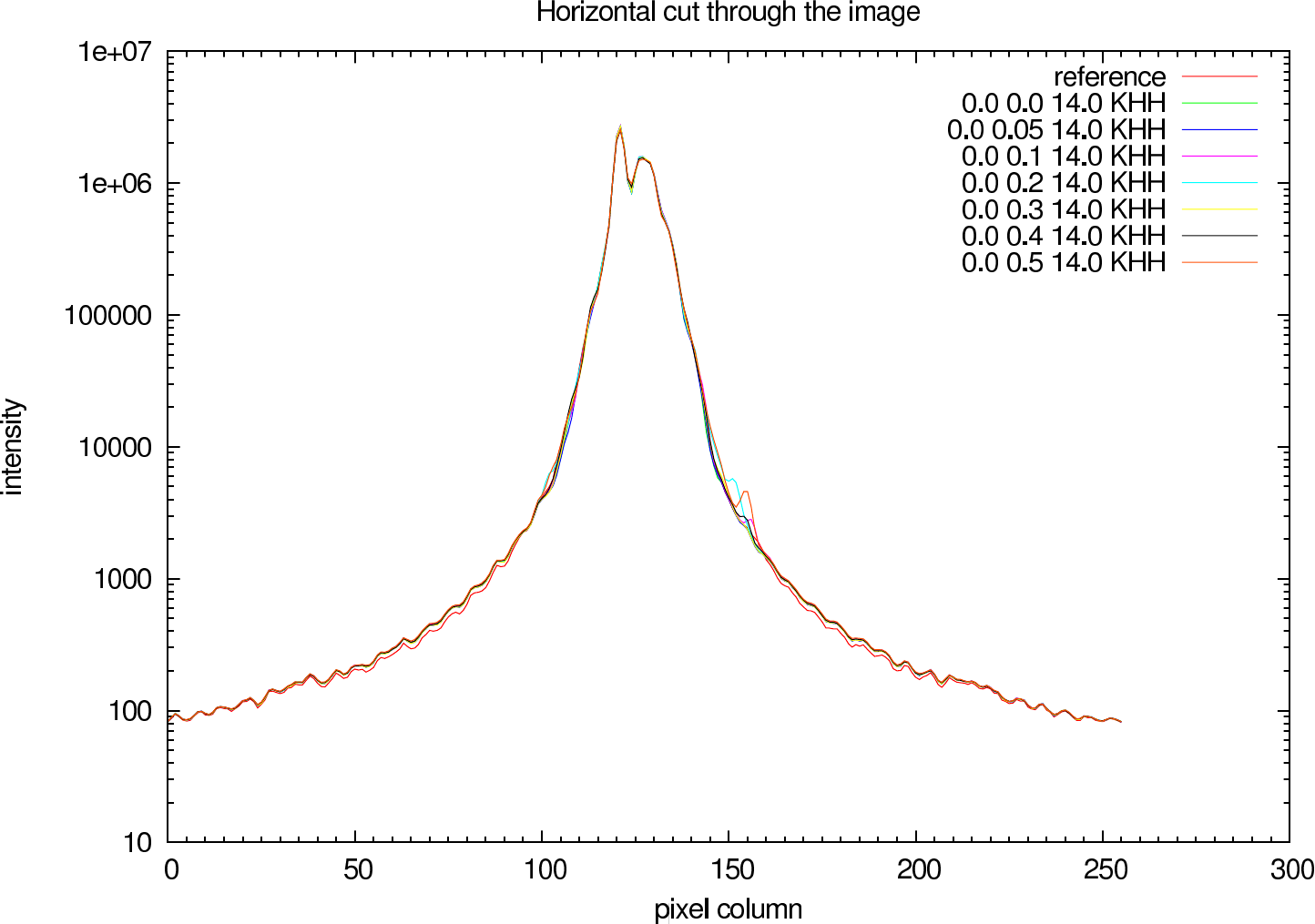 | 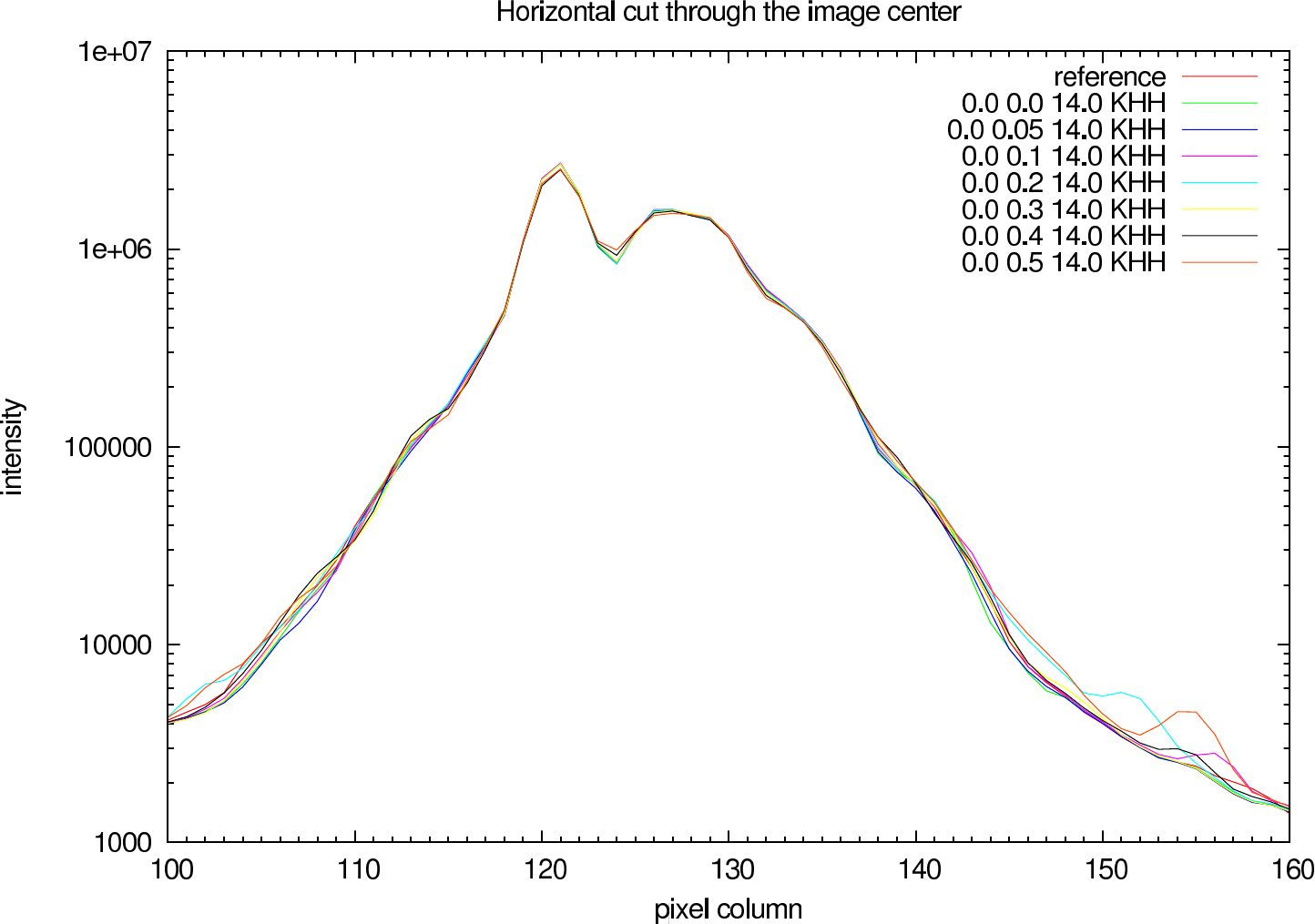 |
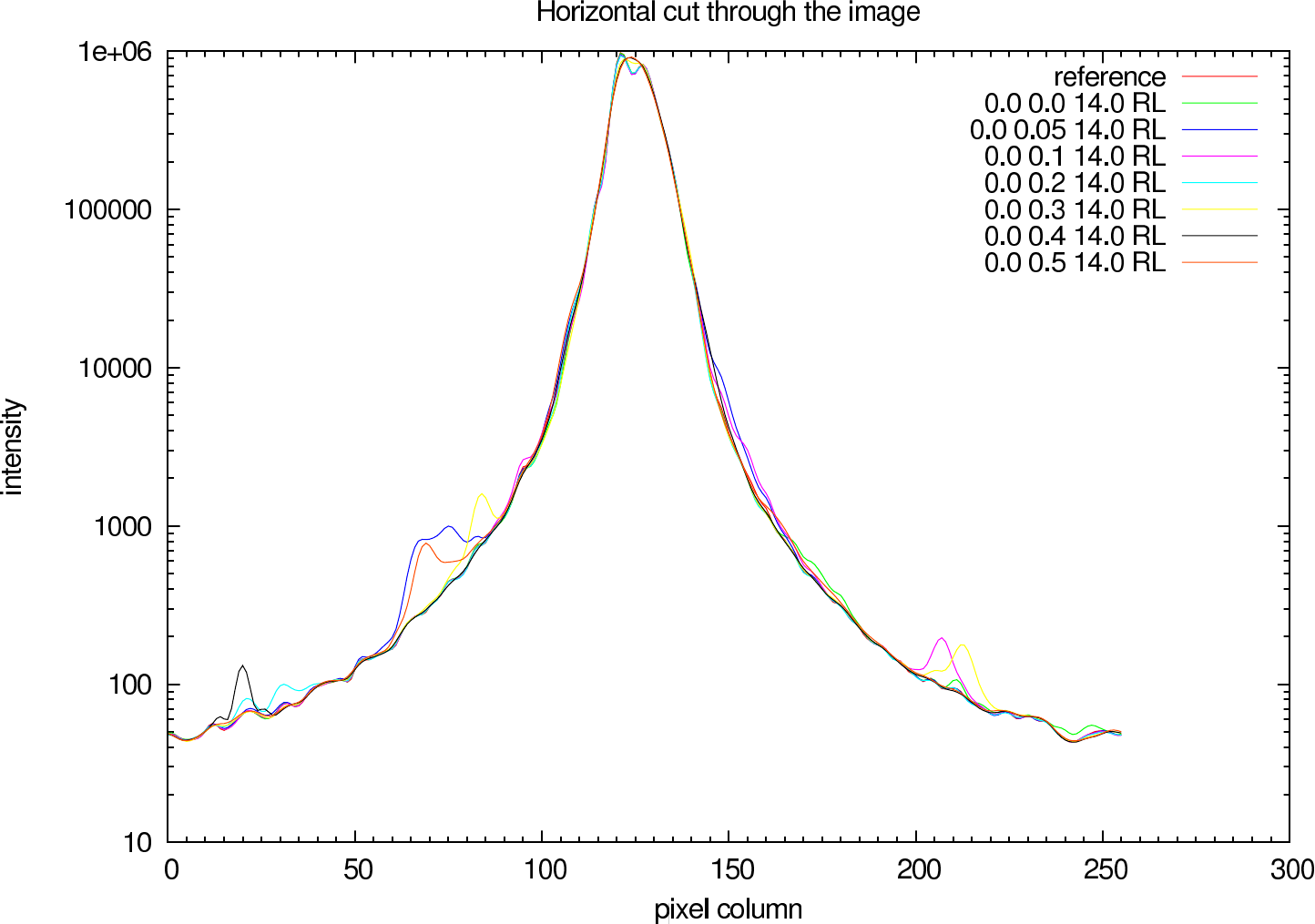 | 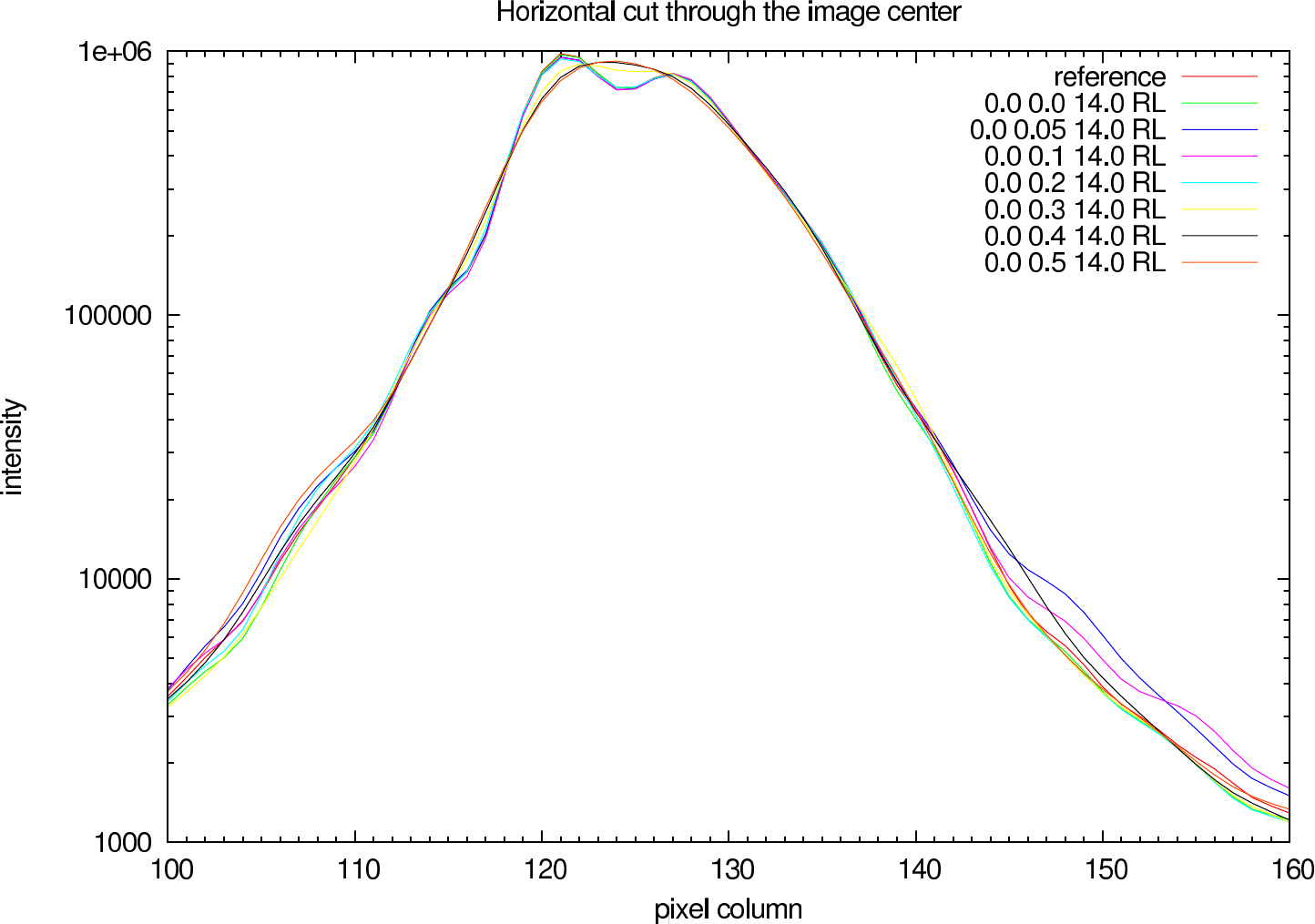 |
 |  |
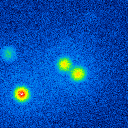
The basis of the simulation is an image of a star cluster (see figure 2). The simulated raw images for a position angle of 108 degree are shown in figure 9.
 |  | 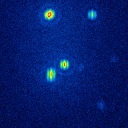 |  |
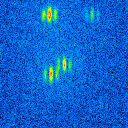 | 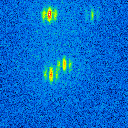 | 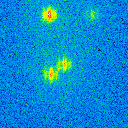 | 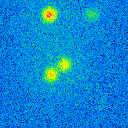 |
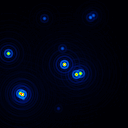
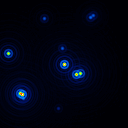
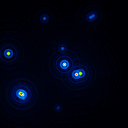
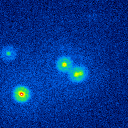
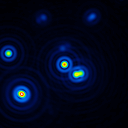
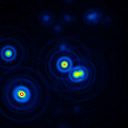
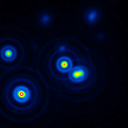
A comparison of the reconstructions depending on the phase error is presented in figure 10 for the J-Band. For the K-Band the results are presented in figure 11.
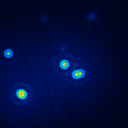 | 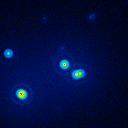 |  |  |
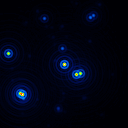 | 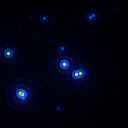 | 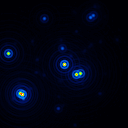 | 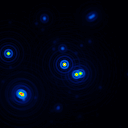 |
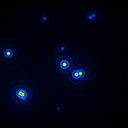 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
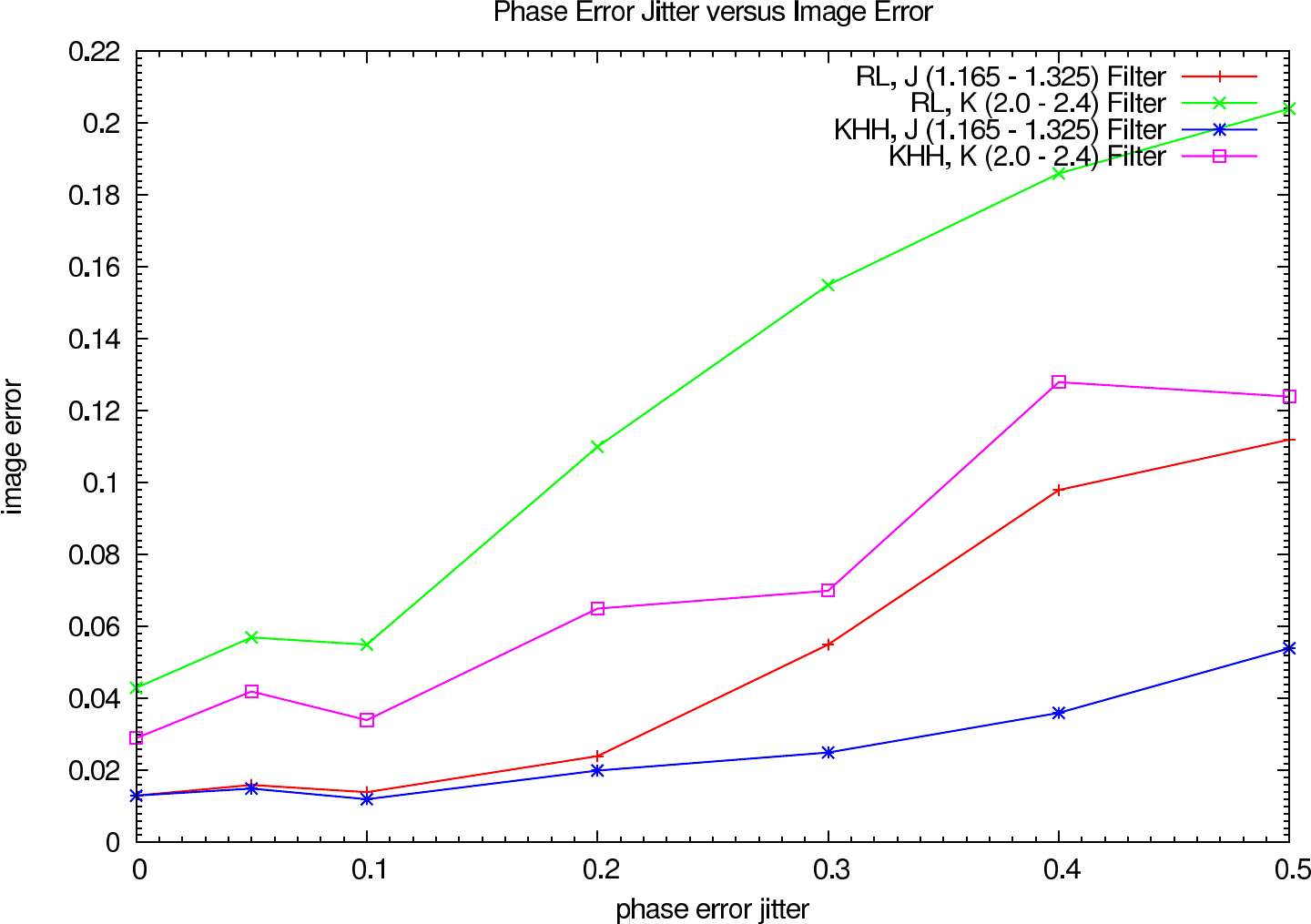
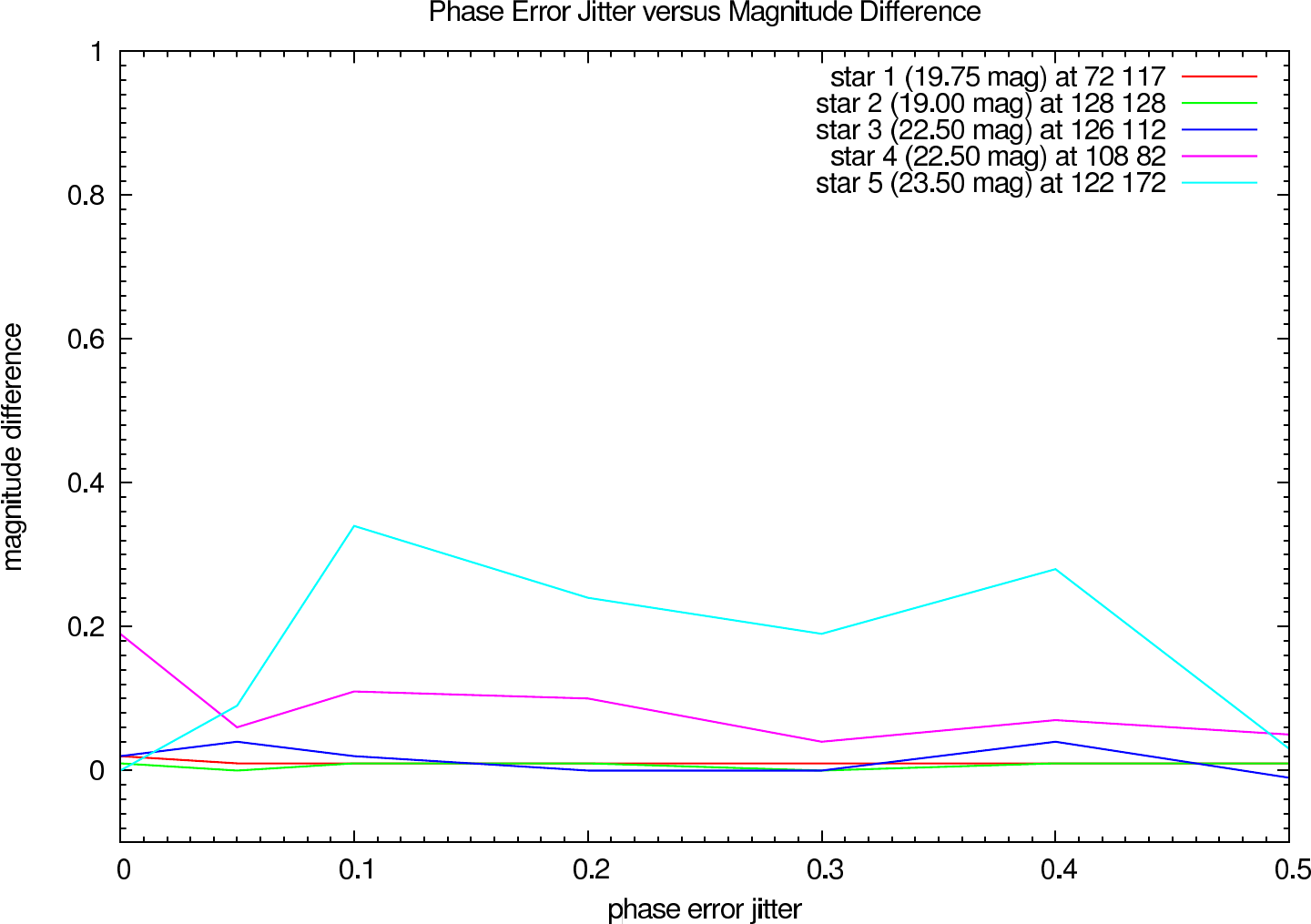
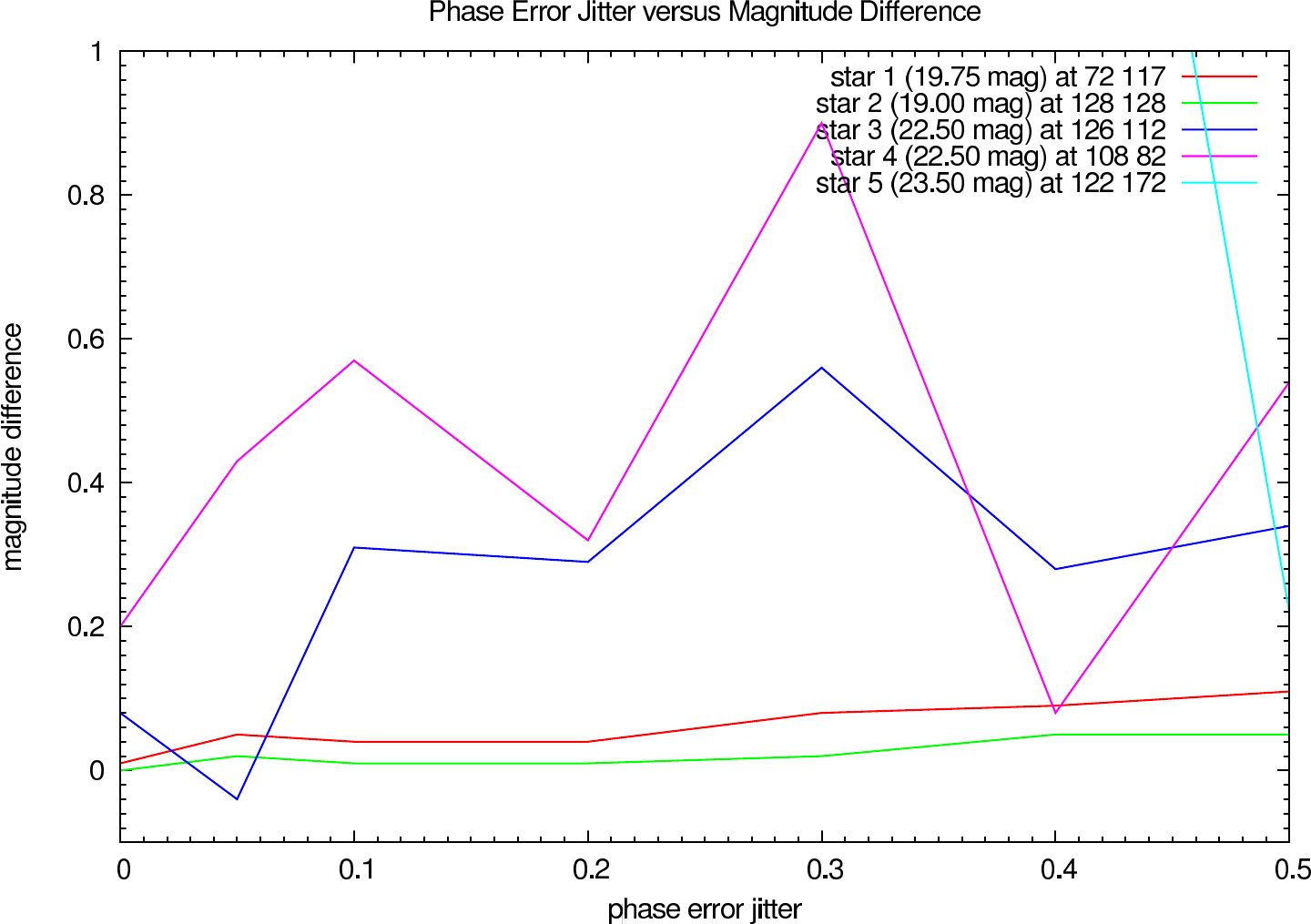
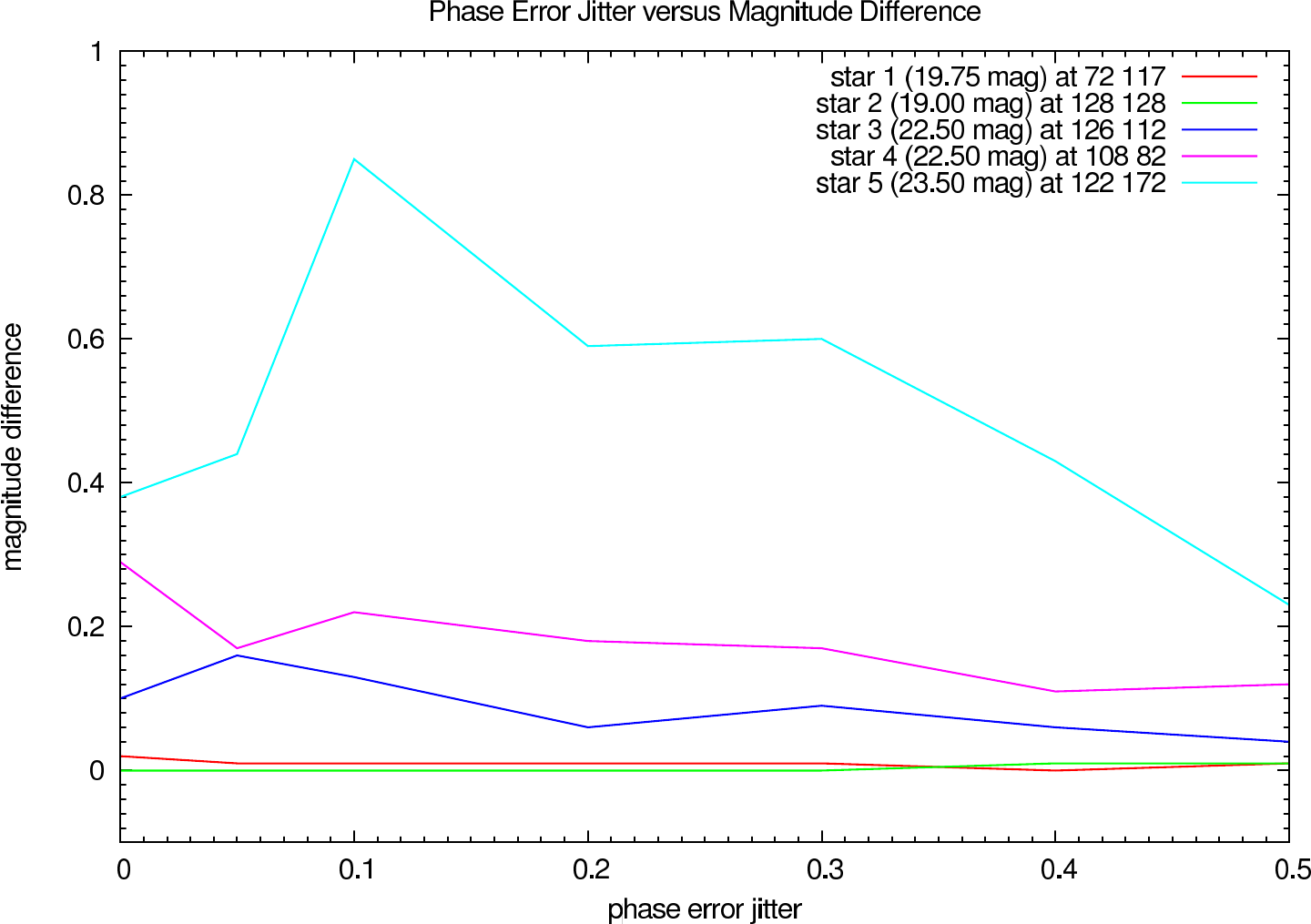
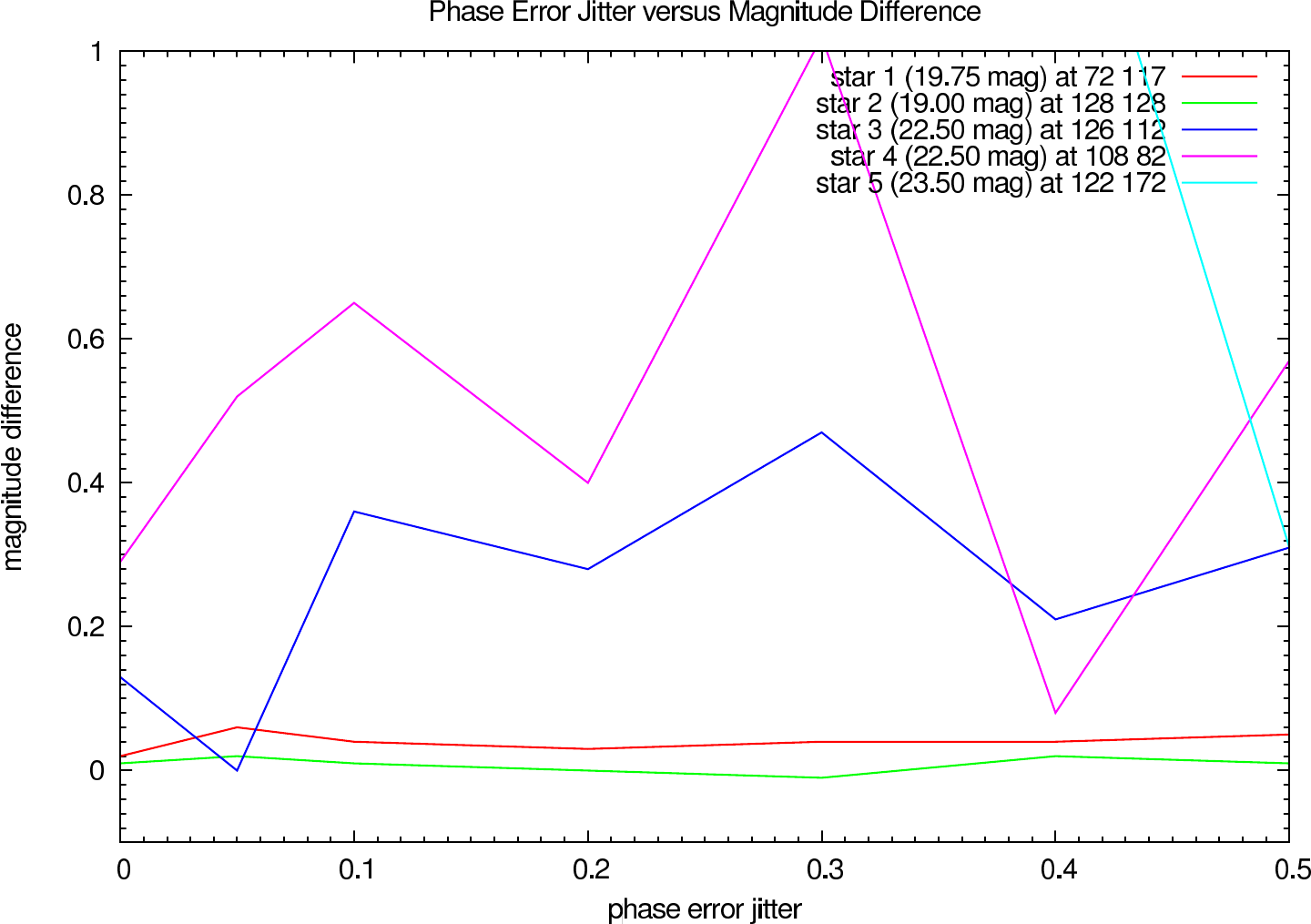
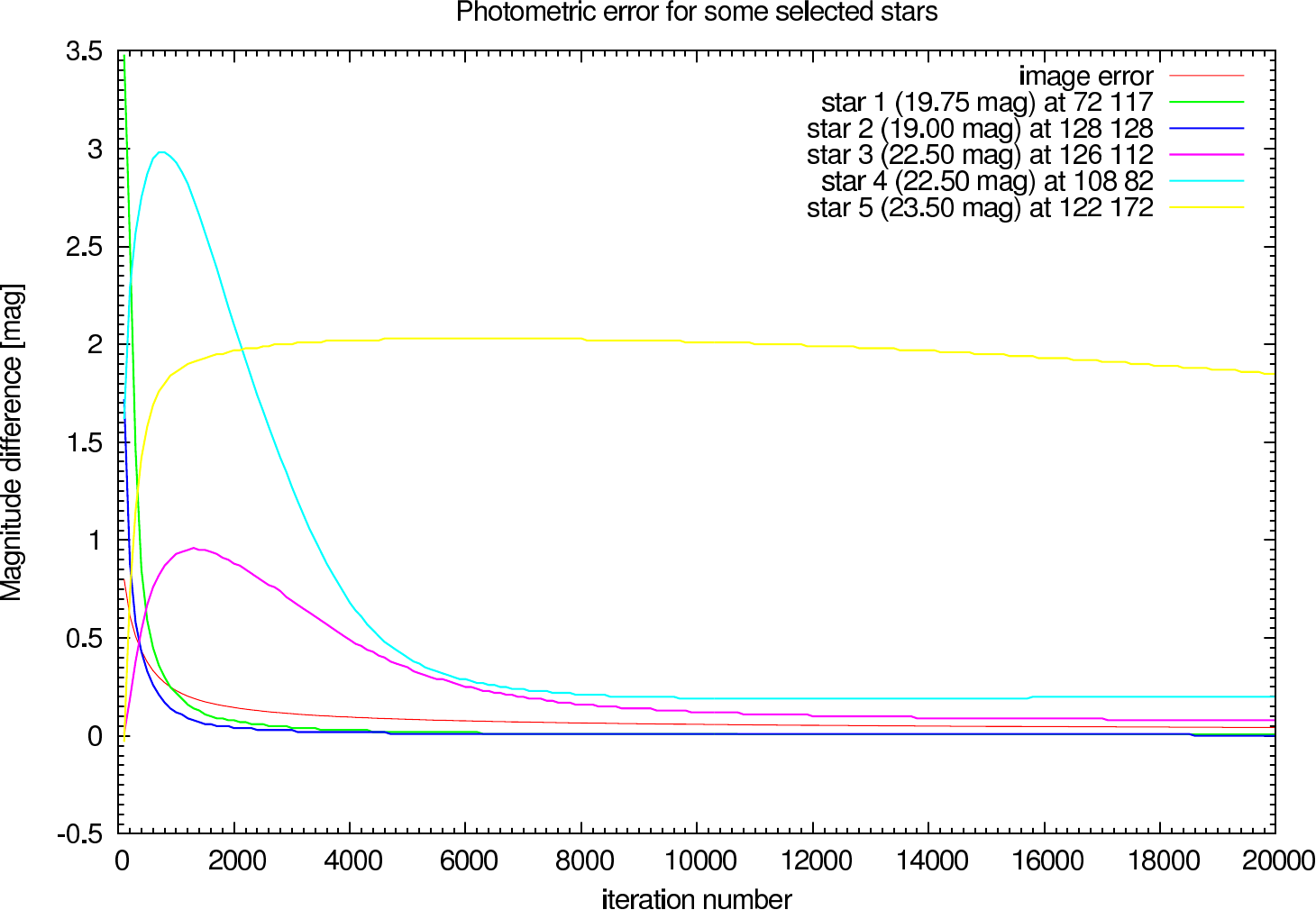
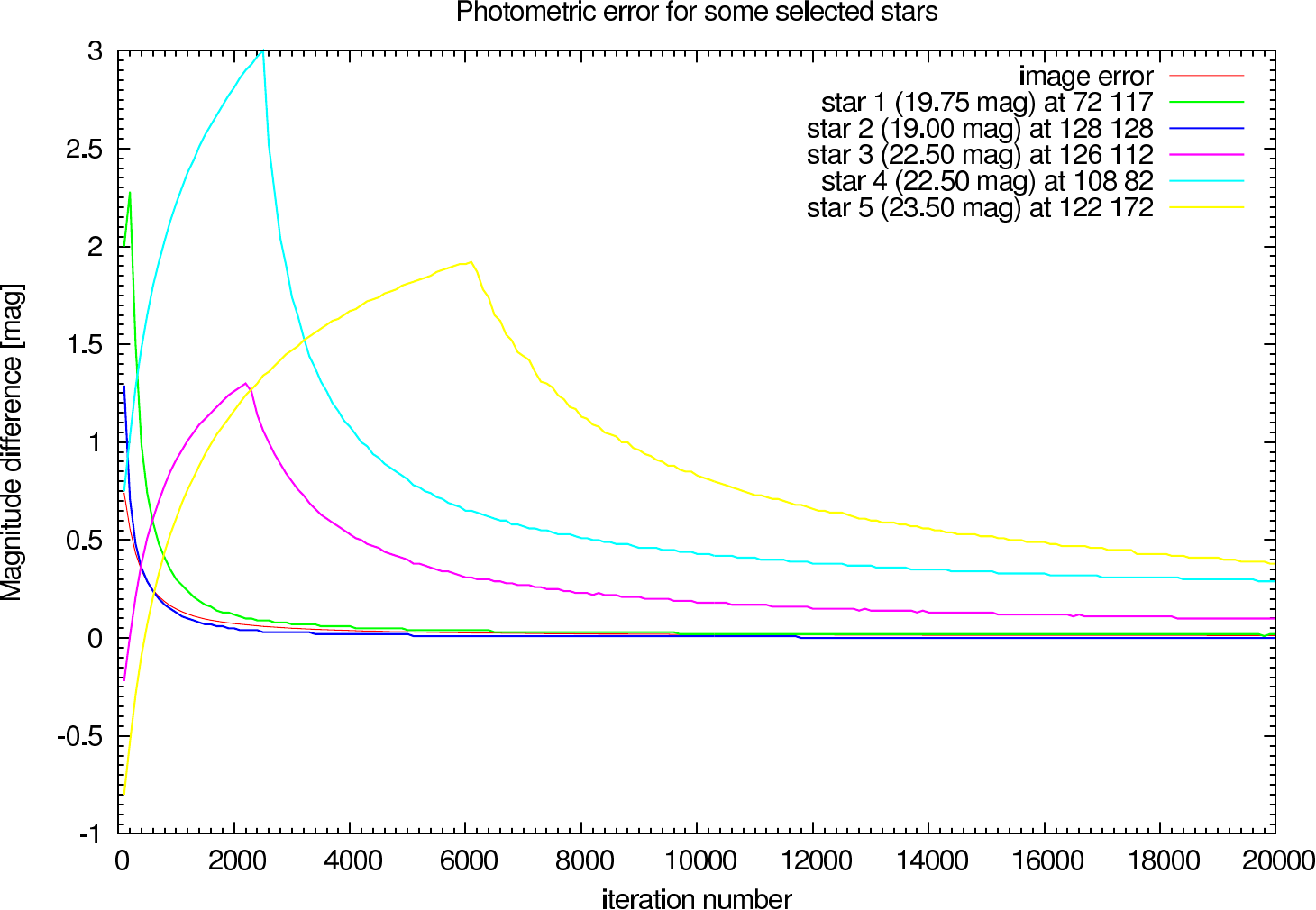
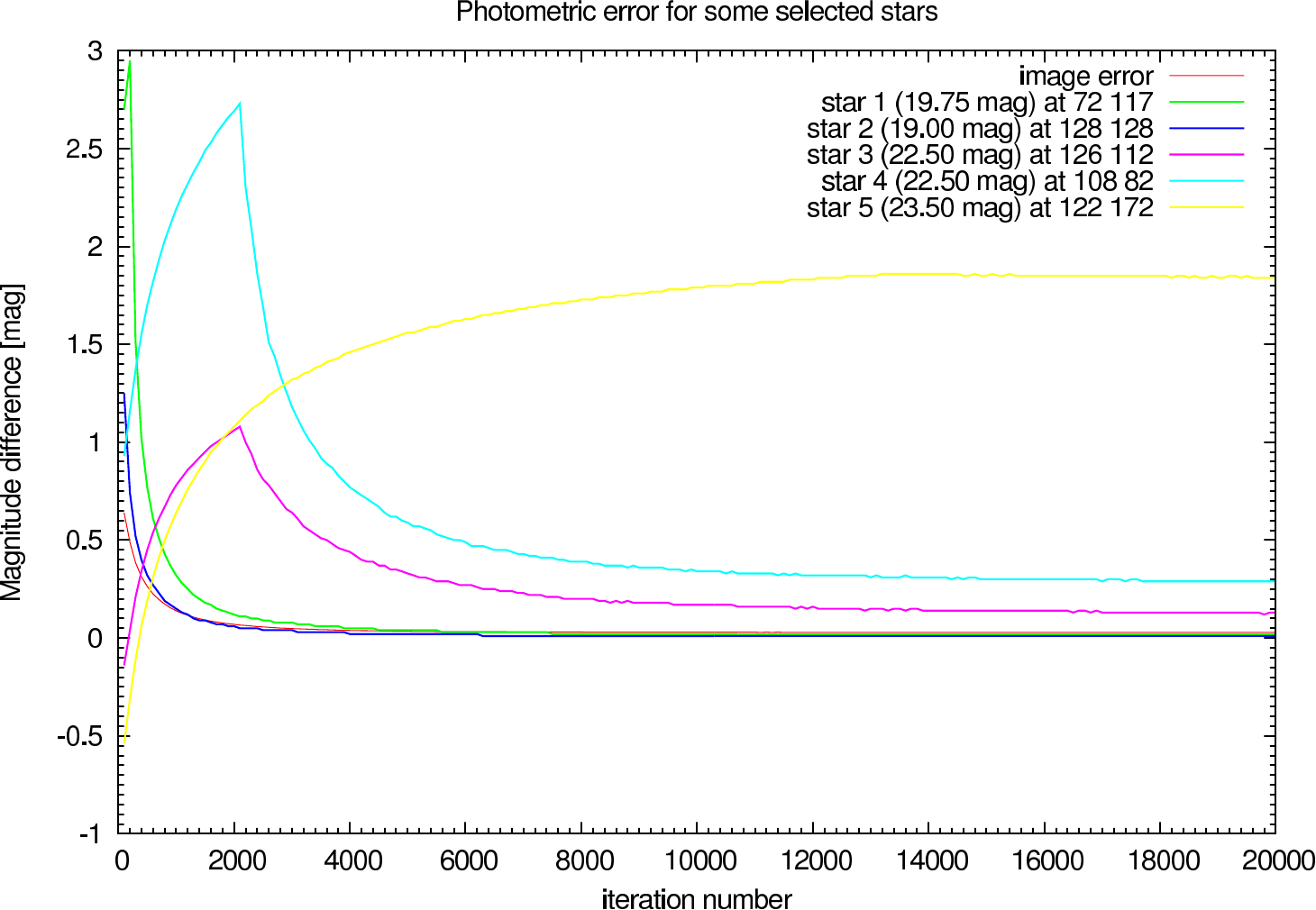
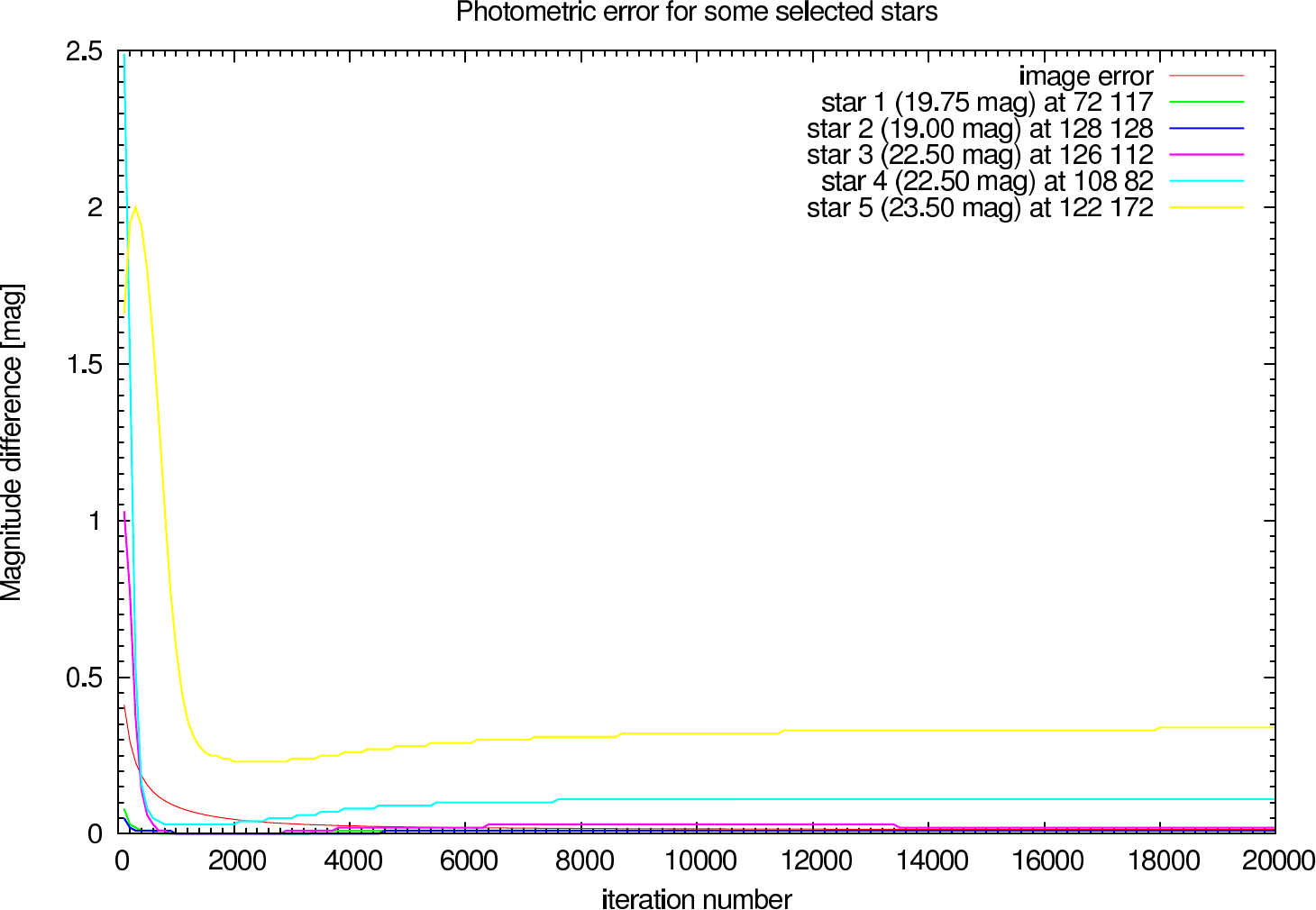
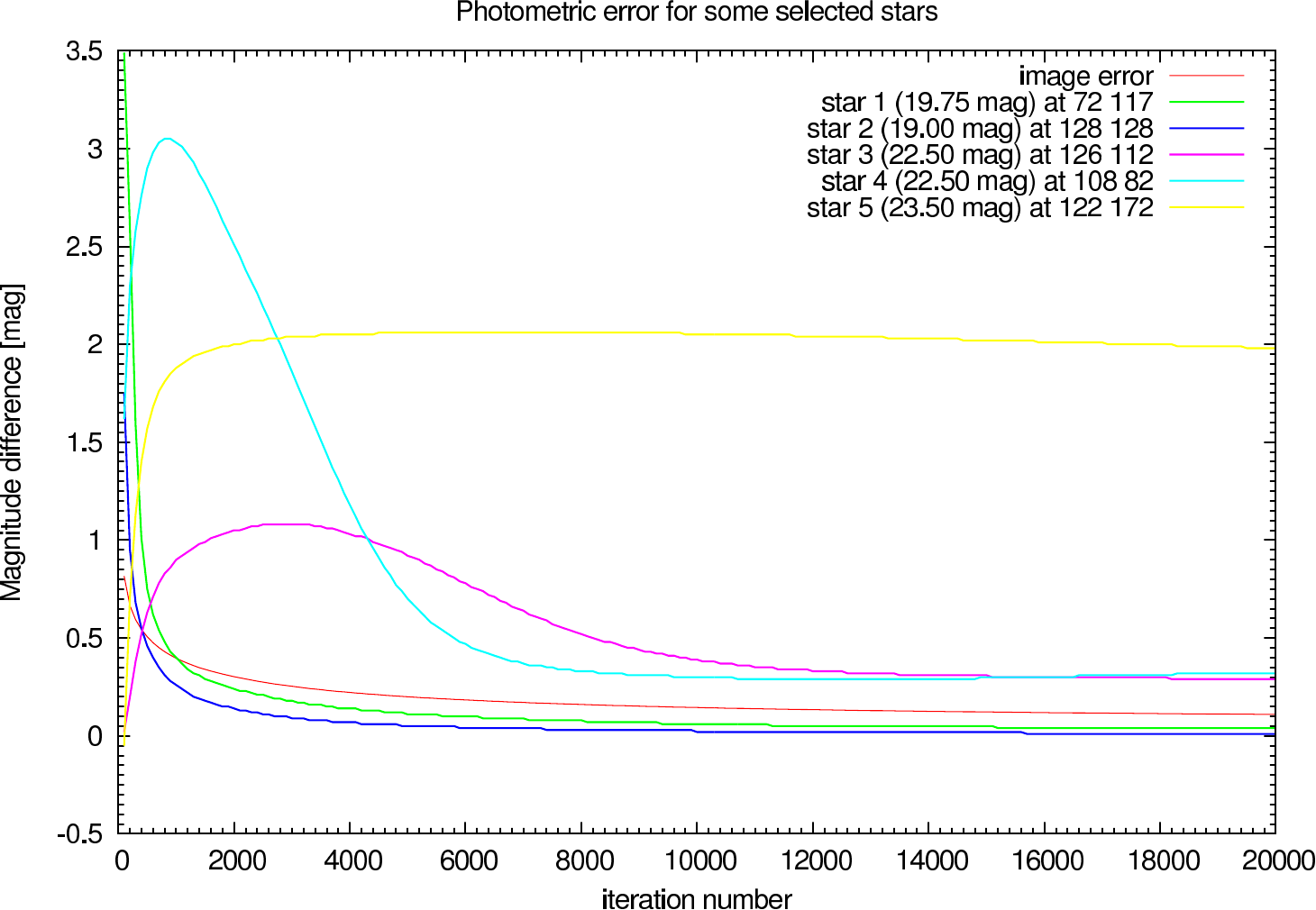
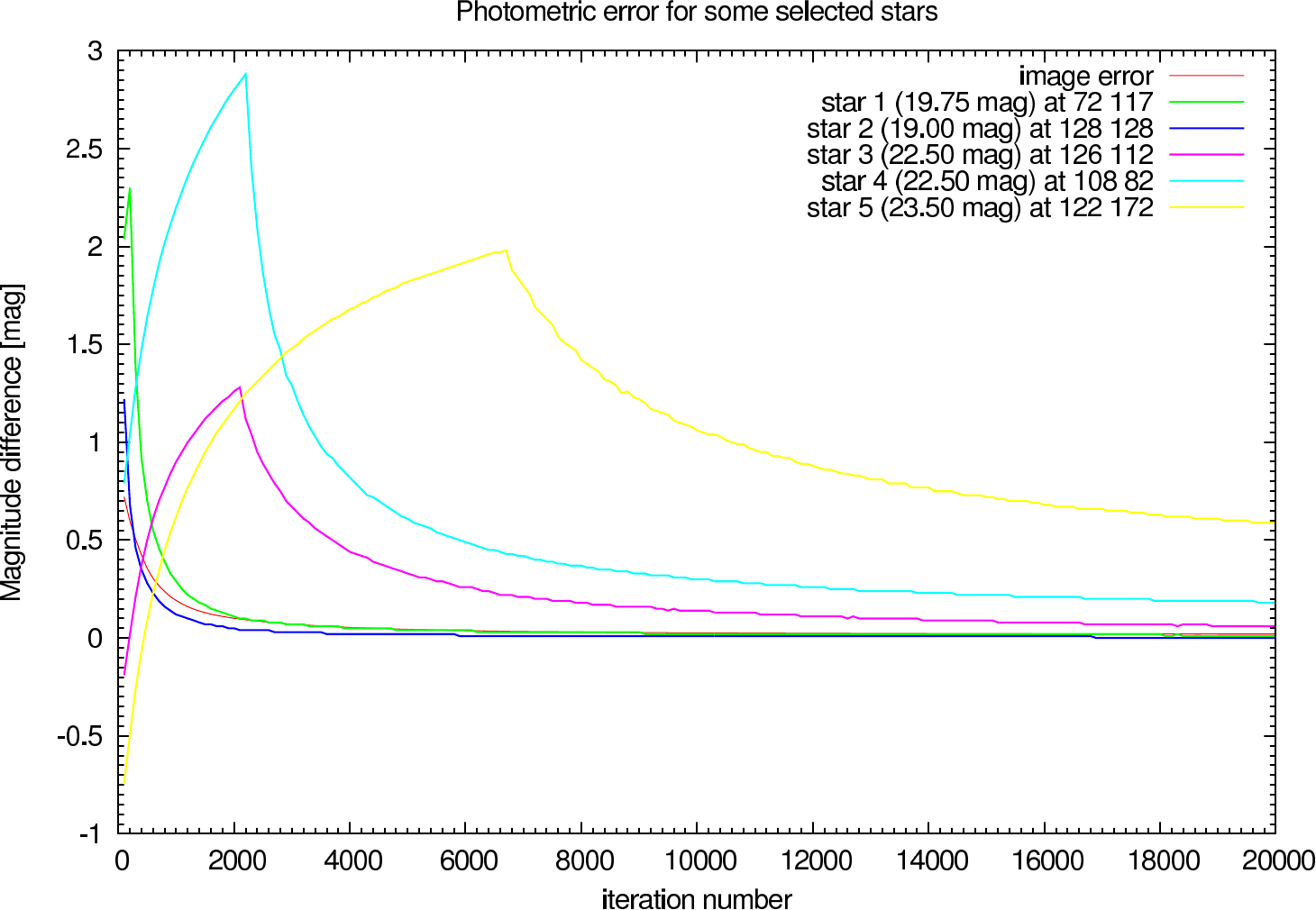
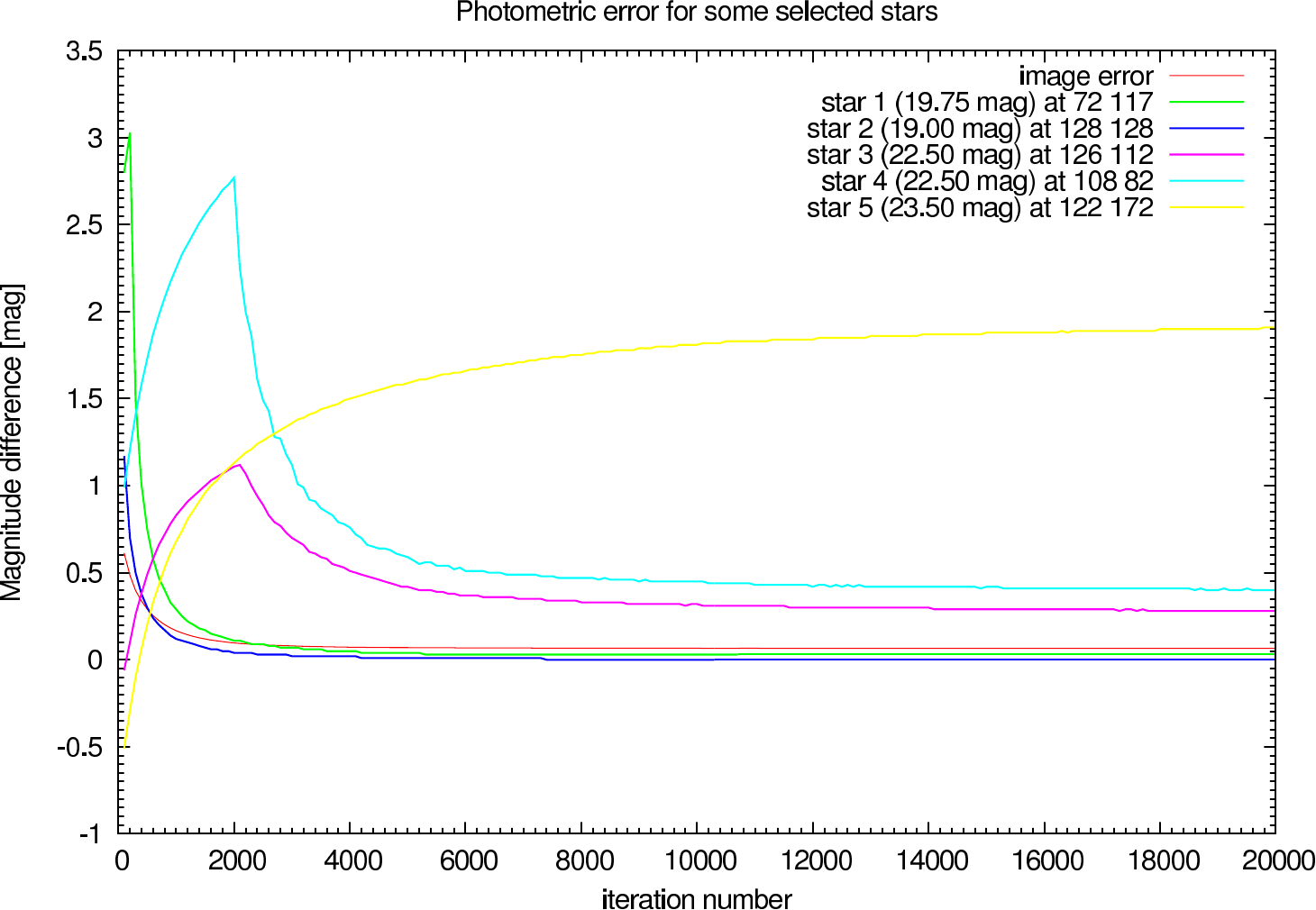
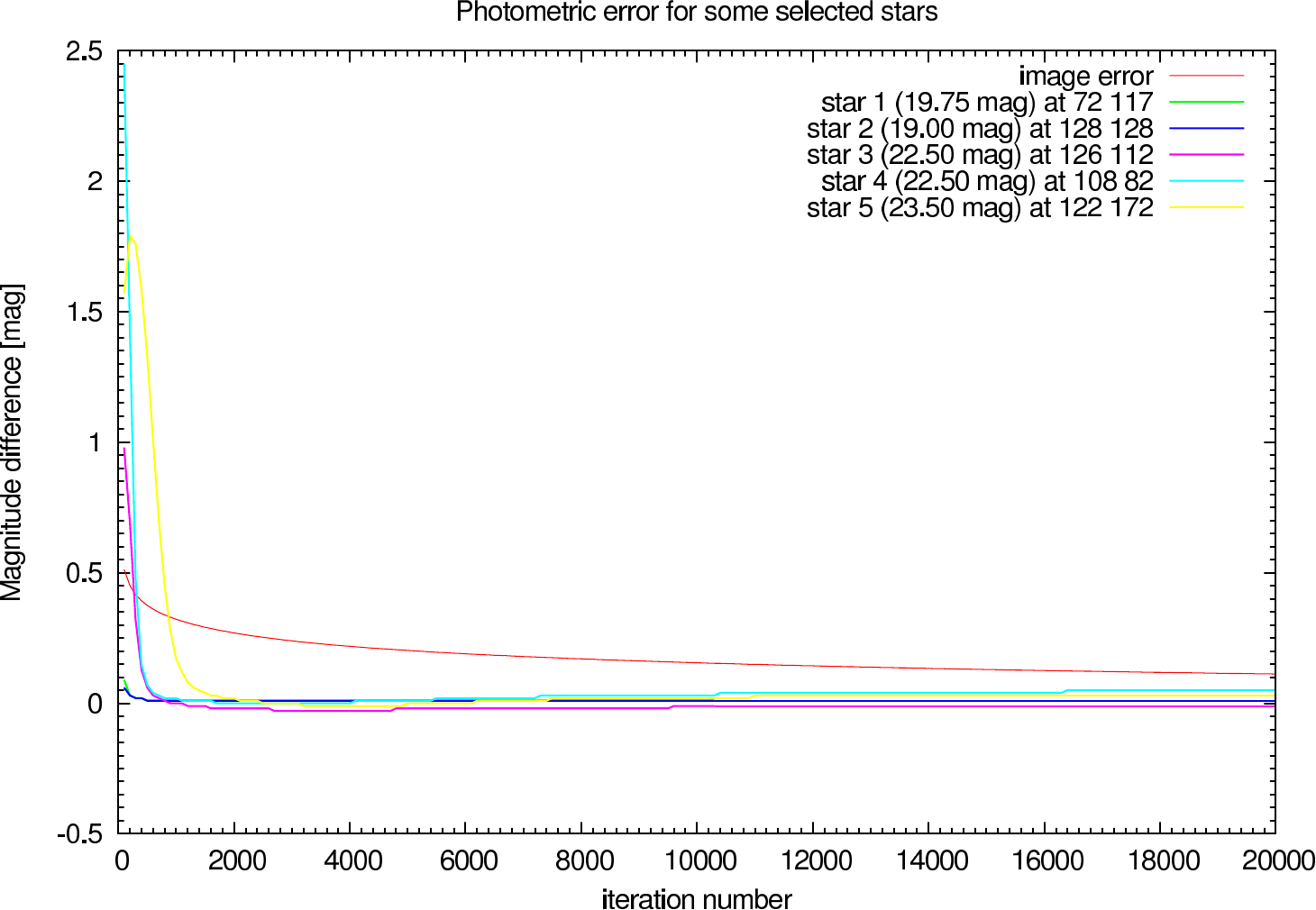
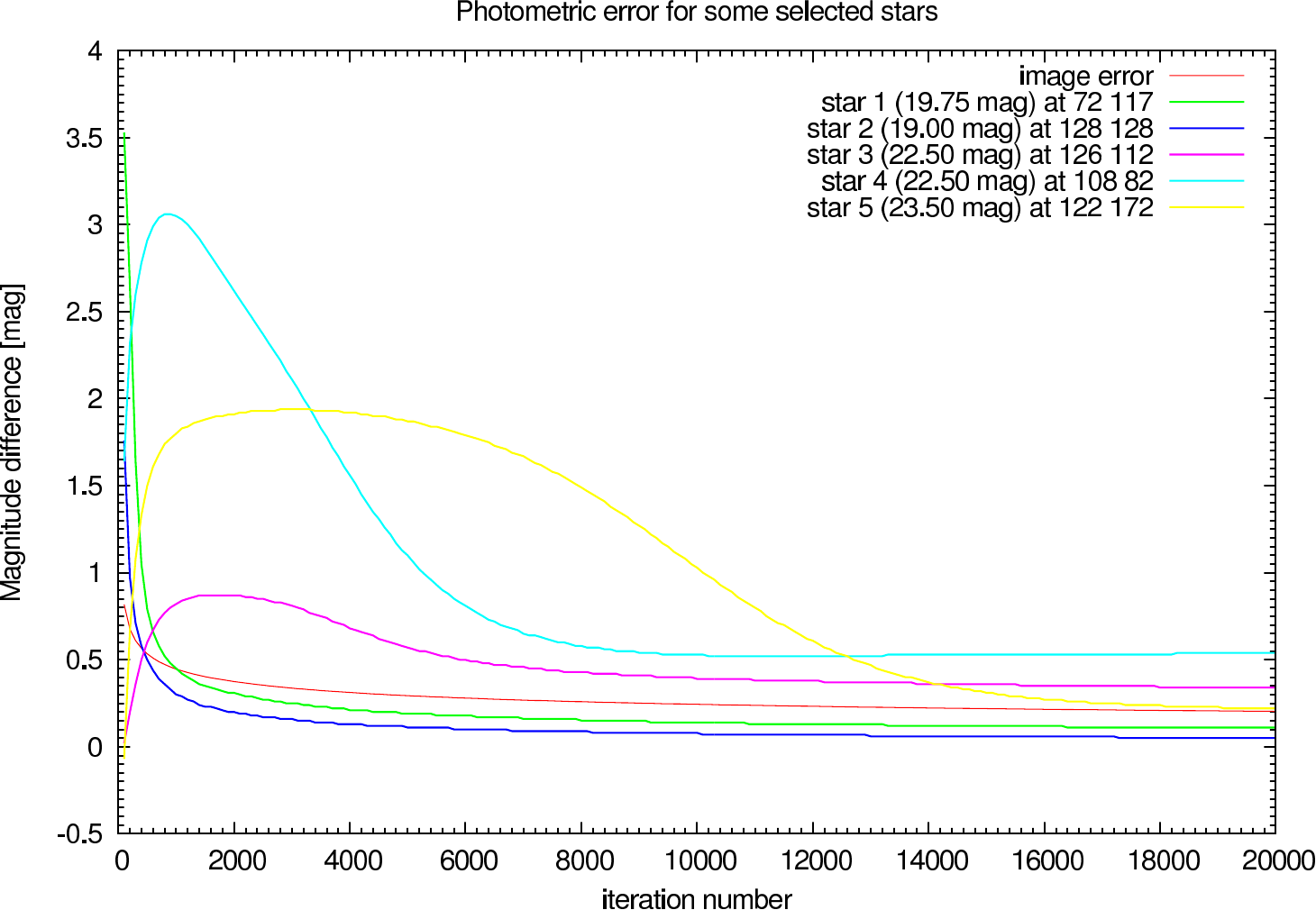
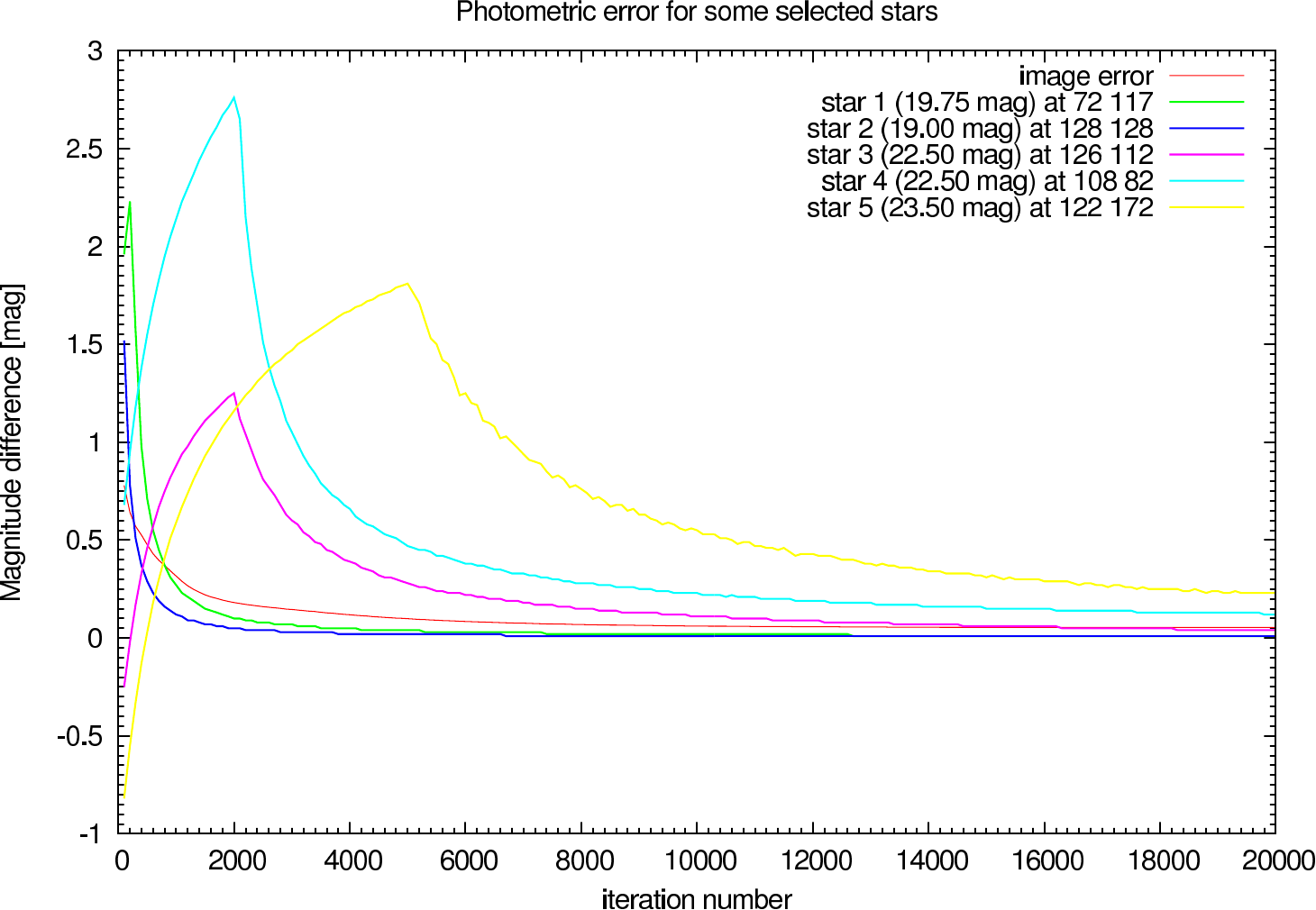
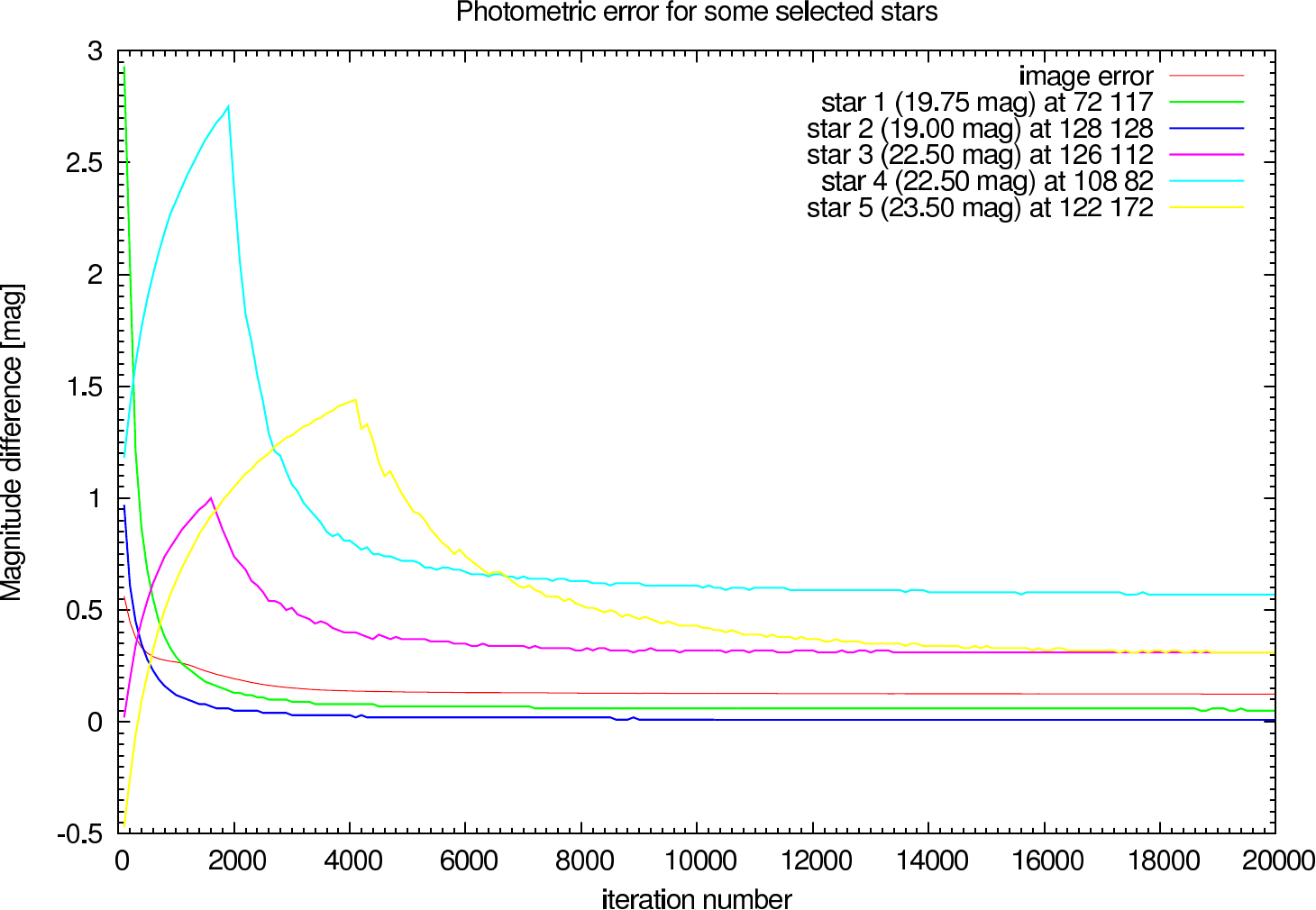
In table 4 (J-Band) and table 5 (K-Band) the errors for the star cluster depending on the OPD error are presented. The image errors are also summarized in figure 12 and the photometric errors in figure 13.
| Testcase | Richardson-Lucy | Building-Block | ||||
|---|---|---|---|---|---|---|
| Phase Error | Image Error | Magnitude Error | Position Error | Image Error | Magnitude Error | Position Error |
| 0.0 0.0 | 0.013 (0.013) | 0.02, 0.01, 0.02, 0.19, 0.00 | 0.00, 0.00, 0.07, 0.08, 0.21 | 0.013 (0.013) | 0.02, 0.00, 0.10, 0.29, 0.38 | 0.00, 0.00, 0.05, 0.01, 0.04 |
| 0.0 0.05 | 0.016 (0.016) | 0.01, 0.00, 0.04, 0.06, 0.09 | 0.01, 0.02, 0.27, 0.05, 0.02 | 0.015 (0.015) | 0.01, -0.00, 0.16, 0.17, 0.44 | 0.01, 0.01, 0.09, 0.01, 0.05 |
| 0.0 0.1 | 0.014 (0.014) | 0.01, 0.01, 0.02, 0.11, 0.34 | 0.01, 0.01, 0.21, 0.06, 0.07 | 0.012 (0.012) | 0.01, 0.00, 0.13, 0.22, 0.85 | 0.00, 0.00, 0.07, 0.01, 0.10 |
| 0.0 0.2 | 0.024 (0.024) | 0.01, 0.01, -0.00, 0.10, 0.24 | 0.00, 0.00, 0.17, 0.14, 0.04 | 0.020 (0.020) | 0.01, 0.00, 0.06, 0.18, 0.59 | 0.00, 0.01, 0.06, 0.10, 0.06 |
| 0.0 0.3 | 0.055 (0.055) | 0.01, 0.00, -0.00, 0.04, 0.19 | 0.01, 0.00, 0.26, 0.17, 0.49 | 0.025 (0.025) | 0.01, 0.00, 0.09, 0.17, 0.60 | 0.00, 0.00, 0.23, 0.08, 0.35 |
| 0.0 0.4 | 0.098 (0.098) | 0.01, 0.01, 0.04, 0.07, 0.28 | 0.01, 0.01, 0.15, 0.20, 0.77 | 0.036 (0.036) | -0.00, 0.01, 0.06, 0.11, 0.43 | 0.01, 0.02, 0.12, 0.17, 0.77 |
| 0.0 0.5 | 0.112 (0.112) | 0.01, 0.01, -0.01, 0.05, 0.03 | 0.01, 0.02, 0.06, 0.02, 0.56 | 0.054 (0.053) | 0.01, 0.01, 0.04, 0.12, 0.23 | 0.01, 0.02, 0.09, 0.00, 0.56 |
| Testcase | Richardson-Lucy | Building-Block | ||||
|---|---|---|---|---|---|---|
| Phase Error | Image Error | Magnitude Error | Position Error | Image Error | Magnitude Error | Position Error |
| 0.0 0.0 | 0.043 (0.043) | 0.01, 0.00, 0.08, 0.20, 1.85 | 0.07, 0.01, 0.69, 1.52, 1.18 | 0.029 (0.029) | 0.02, 0.01, 0.13, 0.29, 1.84 | 0.05, 0.00, 0.77, 1.55, 0.77 |
| 0.0 0.05 | 0.057 (0.057) | 0.05, 0.02, -0.04, 0.43, 2.05 | 0.08, 0.03, 1.16, 0.16, 0.48 | 0.042 (0.042) | 0.06, 0.02, 0.00, 0.52, 1.92 | 0.08, 0.03, 1.11, 0.11, 0.48 |
| 0.0 0.1 | 0.055 (0.055) | 0.04, 0.01, 0.31, 0.57, 1.59 | 0.05, 0.03, 0.75, 1.47, 0.53 | 0.034 (0.034) | 0.04, 0.01, 0.36, 0.65, 1.73 | 0.03, 0.04, 0.51, 1.59, 0.17 |
| 0.0 0.2 | 0.110 (0.110) | 0.04, 0.01, 0.29, 0.32, 1.98 | 0.07, 0.11, 0.26, 0.95, 0.68 | 0.065 (0.065) | 0.03, 0.00, 0.28, 0.40, 1.91 | 0.07, 0.10, 0.28, 0.94, 0.57 |
| 0.0 0.3 | 0.155 (0.155) | 0.08, 0.02, 0.56, 0.90, 2.08 | 0.12, 0.05, 1.77, 1.08, 0.40 | 0.070 (0.070) | 0.04, -0.01, 0.47, 1.02, 1.93 | 0.12, 0.04, 2.24, 1.58, 0.44 |
| 0.0 0.4 | 0.186 (0.186) | 0.09, 0.05, 0.28, 0.08, 2.09 | 0.09, 0.02, 1.20, 0.86, 0.40 | 0.128 (0.128) | 0.04, 0.02, 0.21, 0.08, 1.37 | 0.10, 0.03, 1.37, 0.90, 1.33 |
| 0.0 0.5 | 0.204 (0.204) | 0.11, 0.05, 0.34, 0.54, 0.22 | 0.06, 0.02, 2.20, 0.95, 1.53 | 0.124 (0.124) | 0.05, 0.01, 0.31, 0.57, 0.31 | 0.07, 0.02, 2.77, 1.00, 1.61 |
 |
 |  |
 |  |
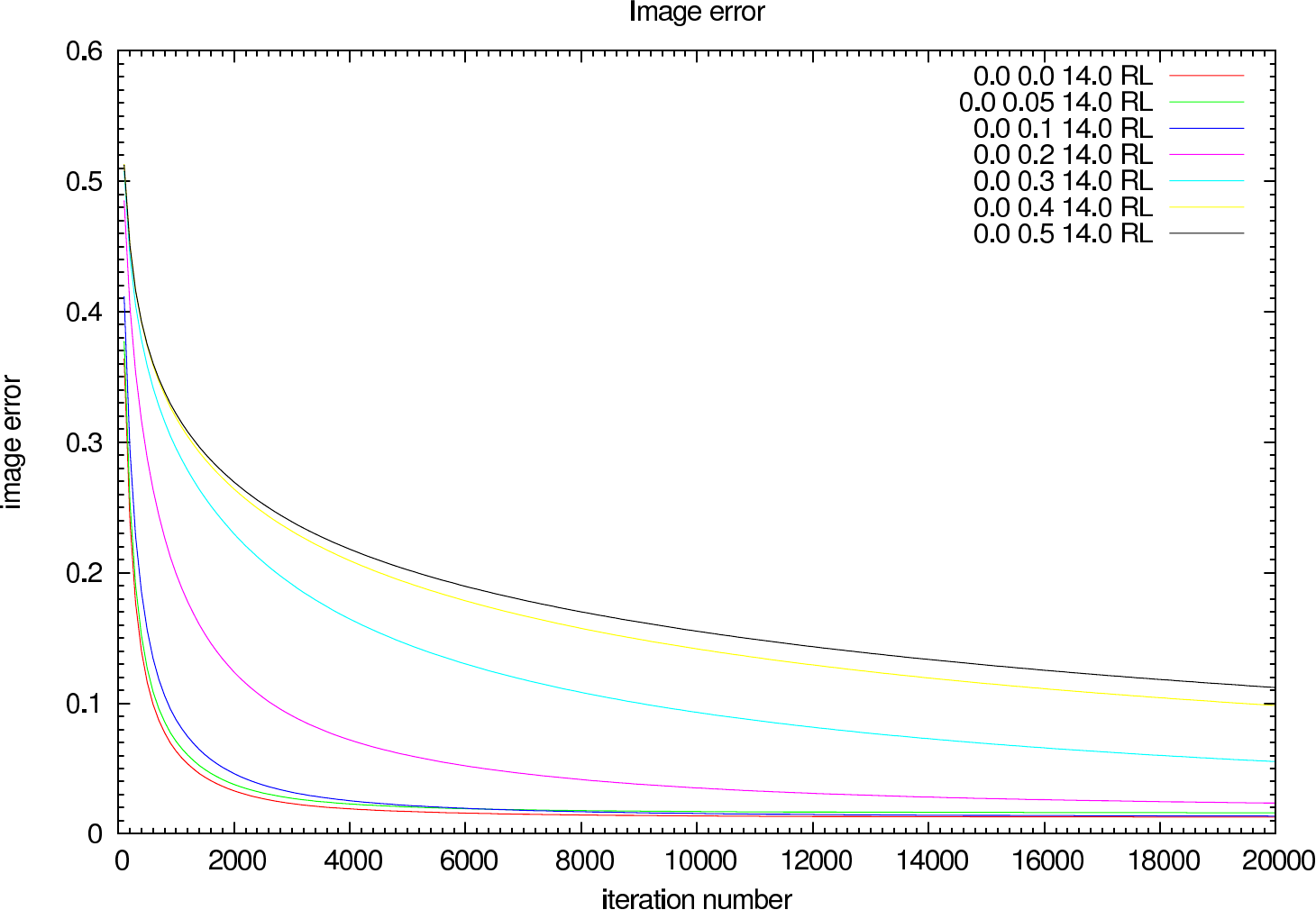
In figure 14 the image error describing the difference between the reconstruction and the reference image is shown for each iteration (in steps of 100 iterations). The effect of the OPD error on the reconstruction error and the optimal iteration number is clearly visible.
 | 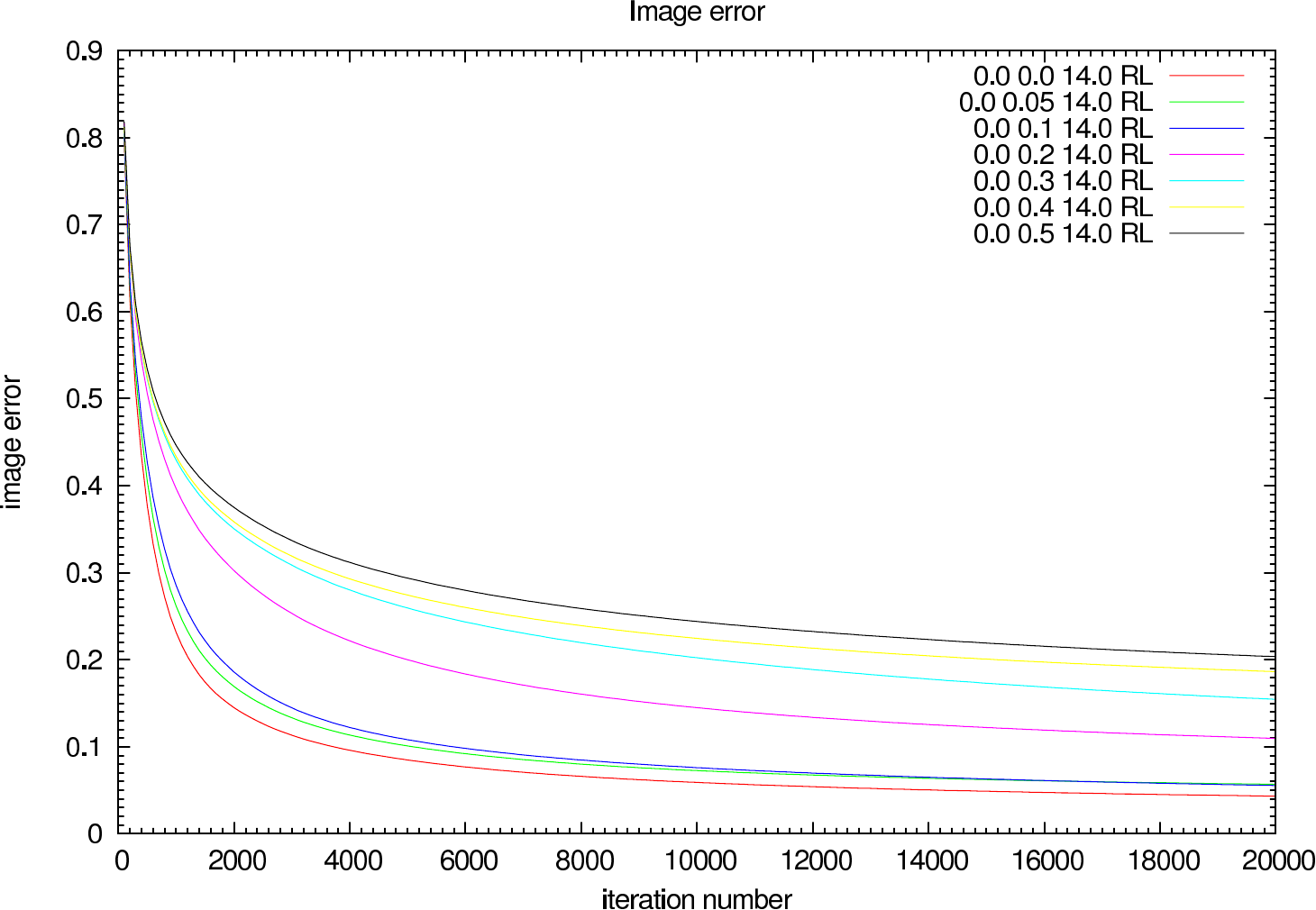 |
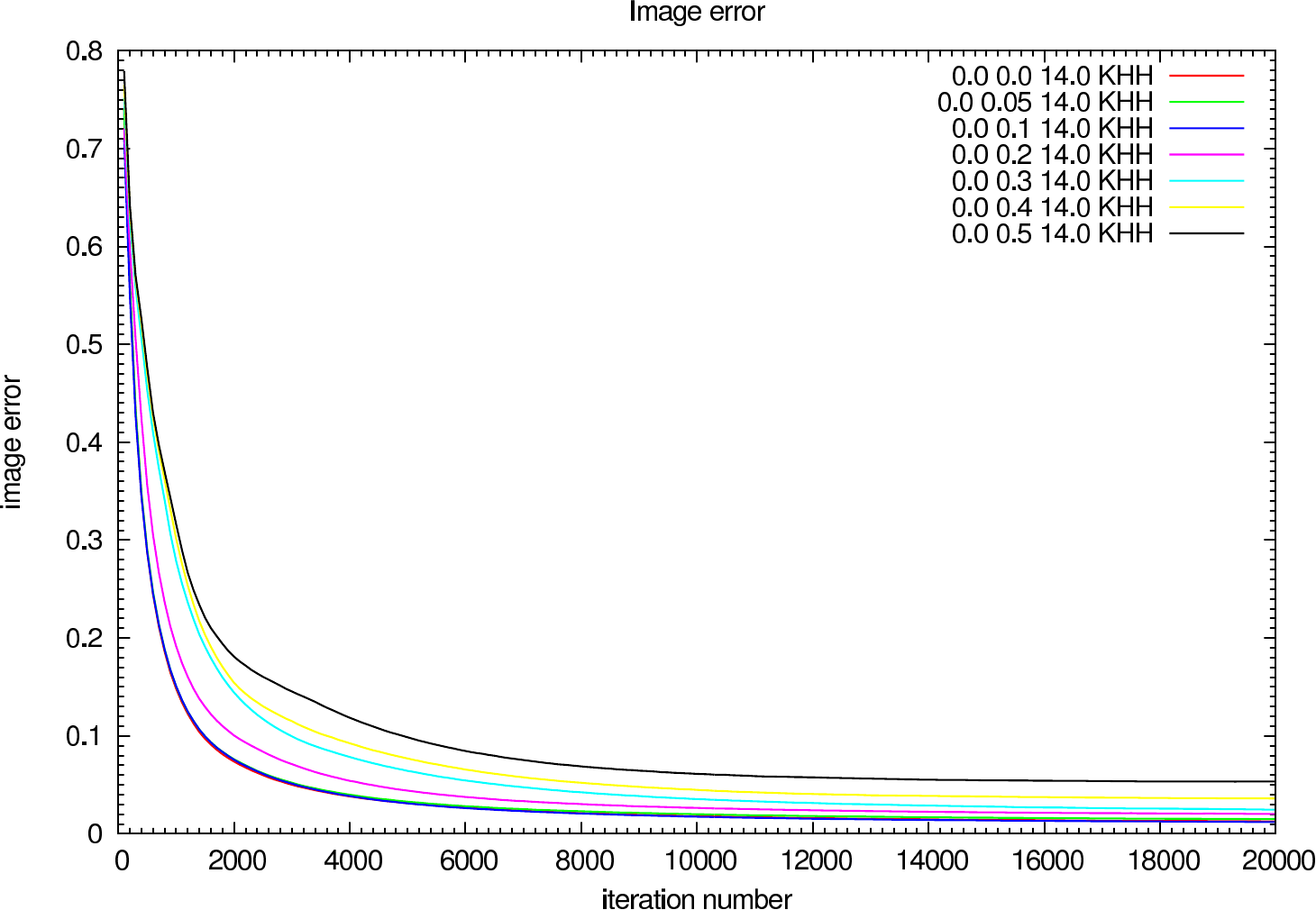 | 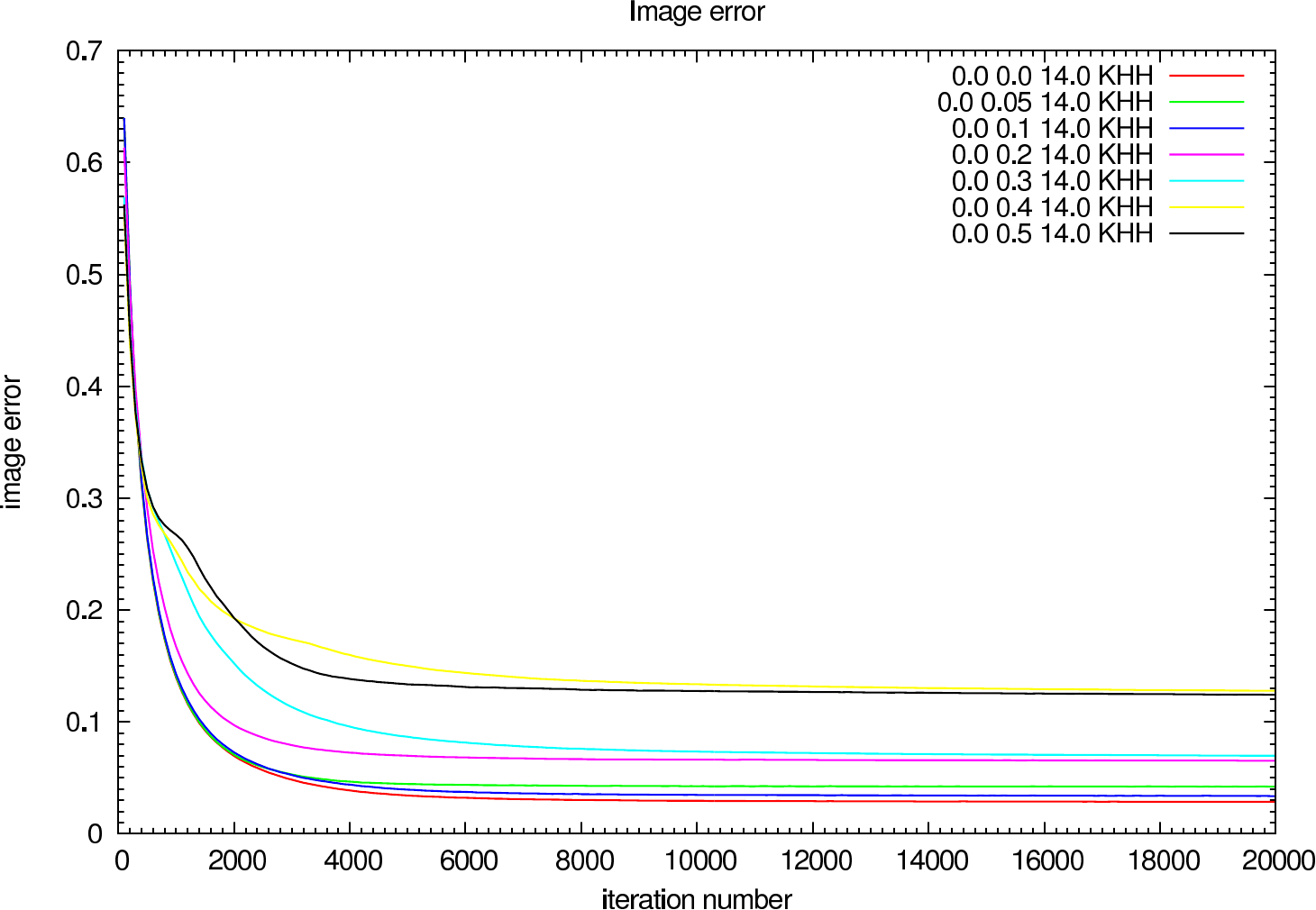 |
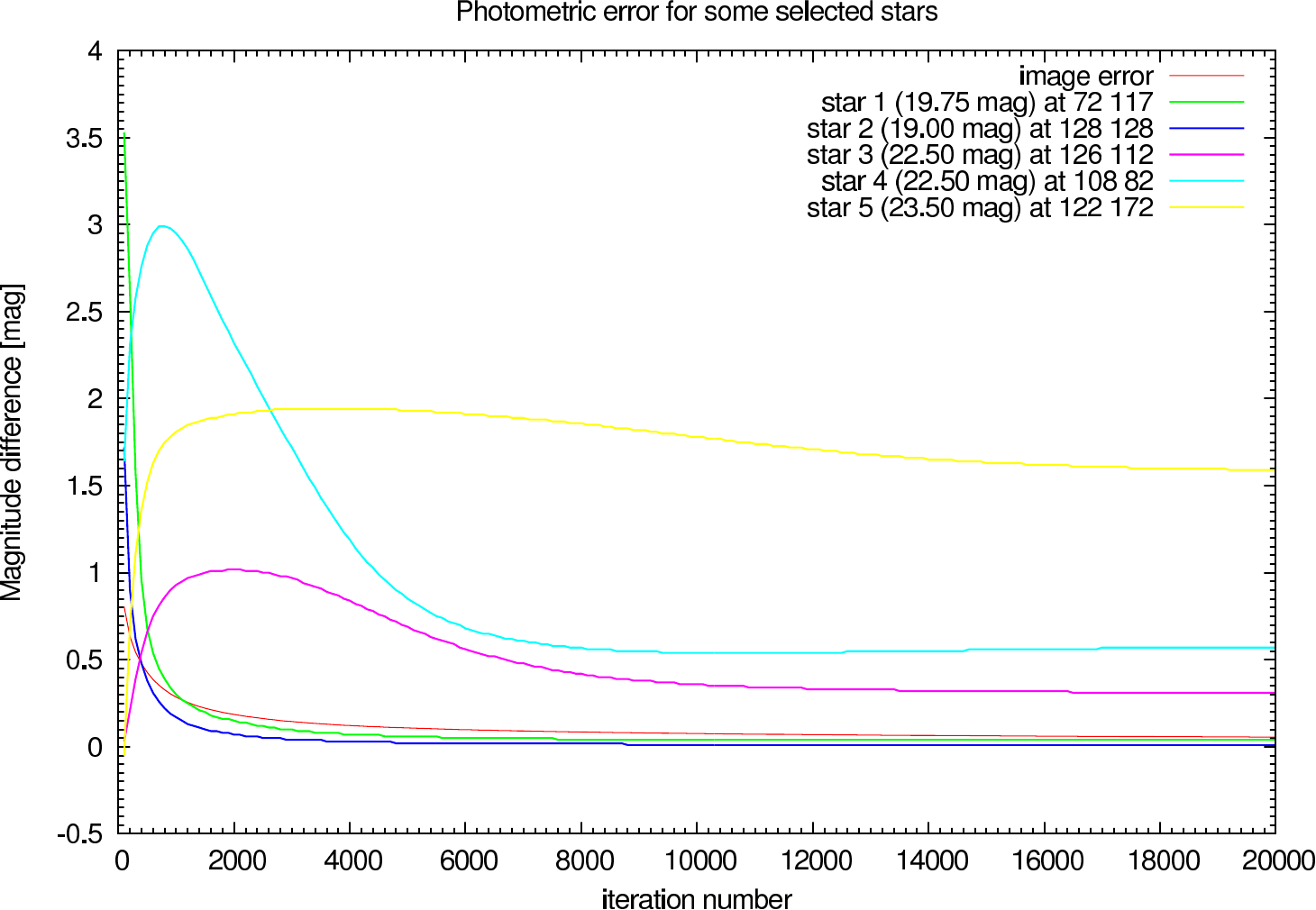
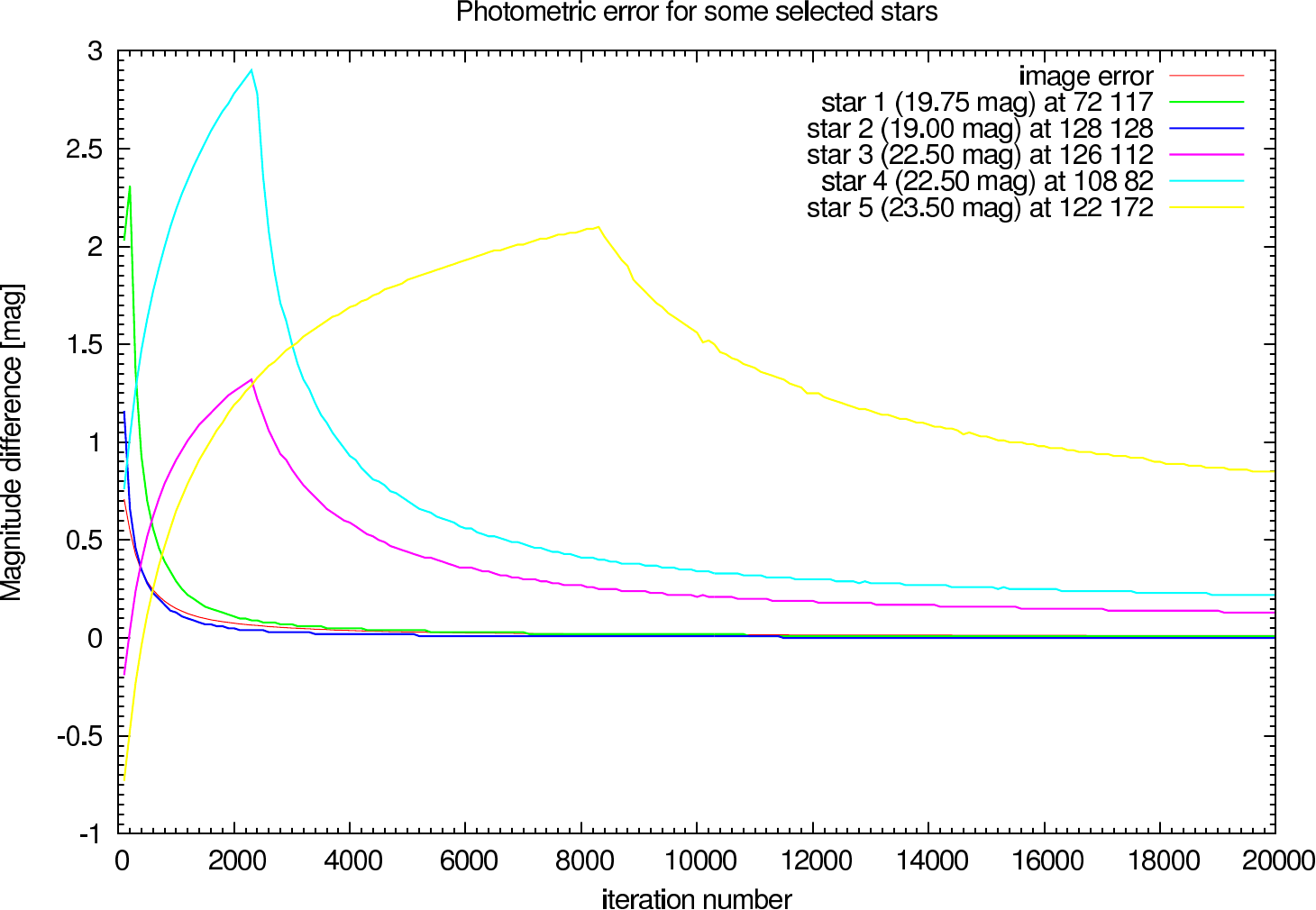
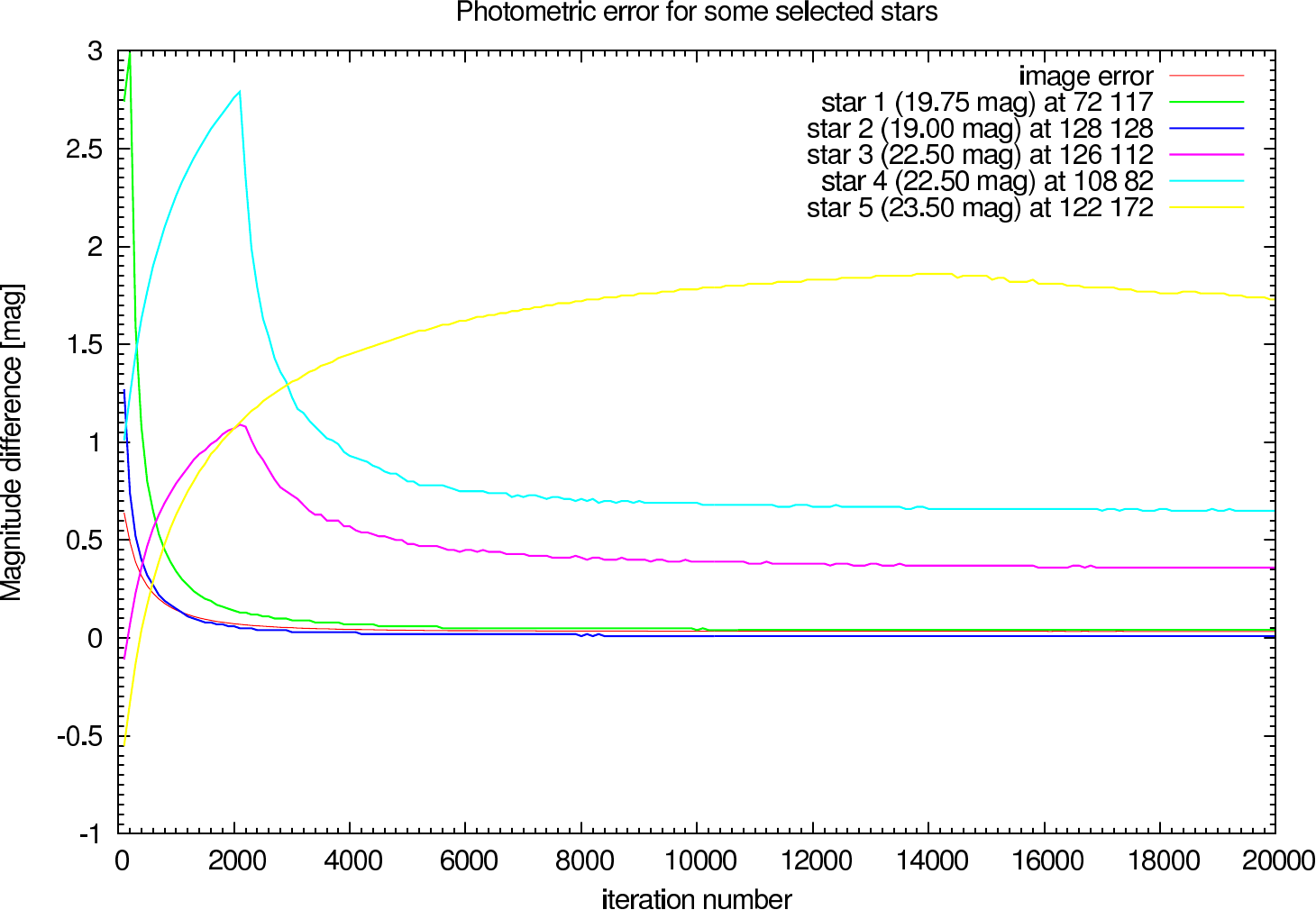
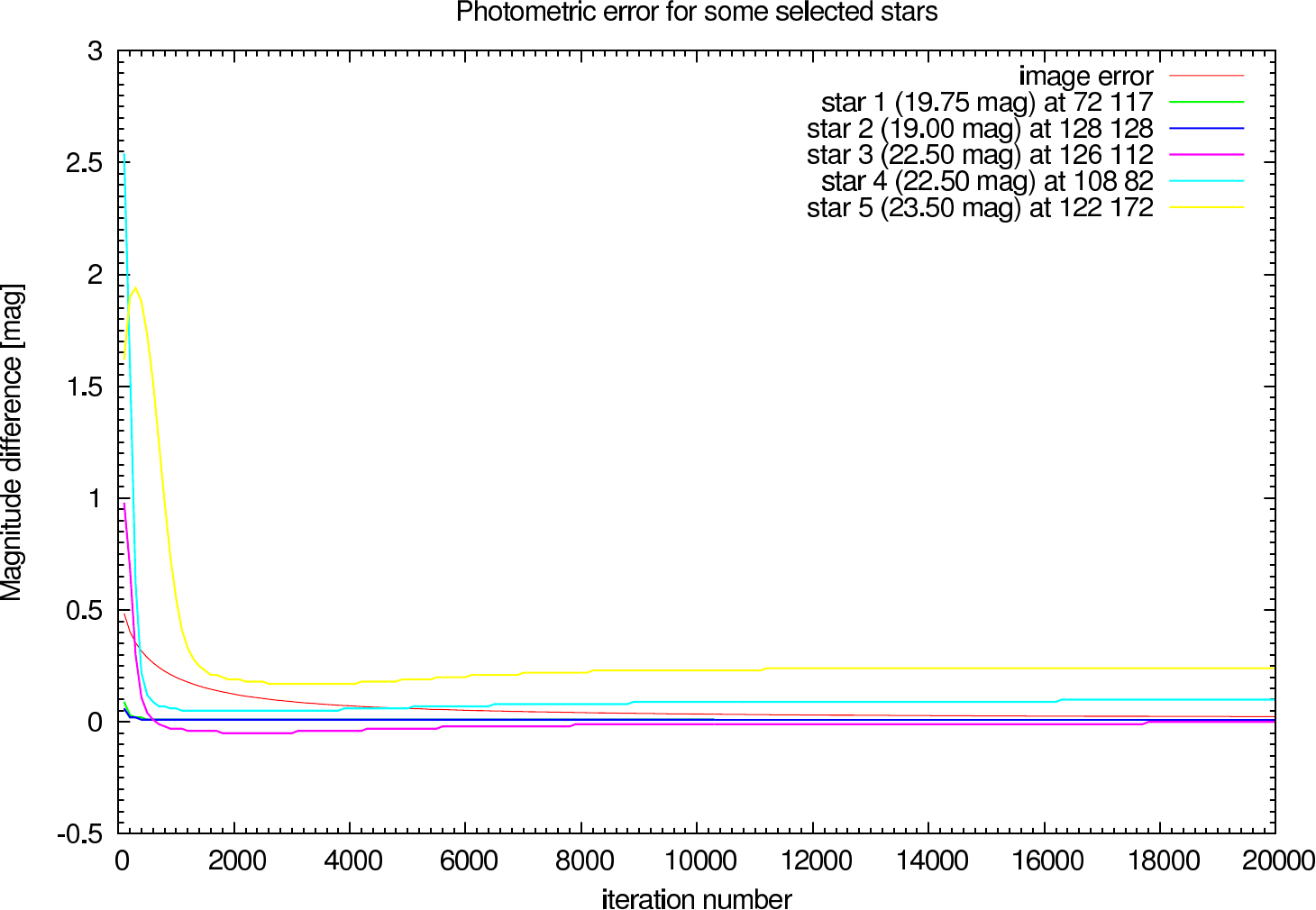
In the figures figure 15, figure 16, figure 17, and figure 18 the image and photometric errors depending on the calibrator strehl and the iteration number is shown. The overall shape is the same, but the optimum number of iterations is difficult to select, because not all photometric errors have their minimum at the same iteration number.
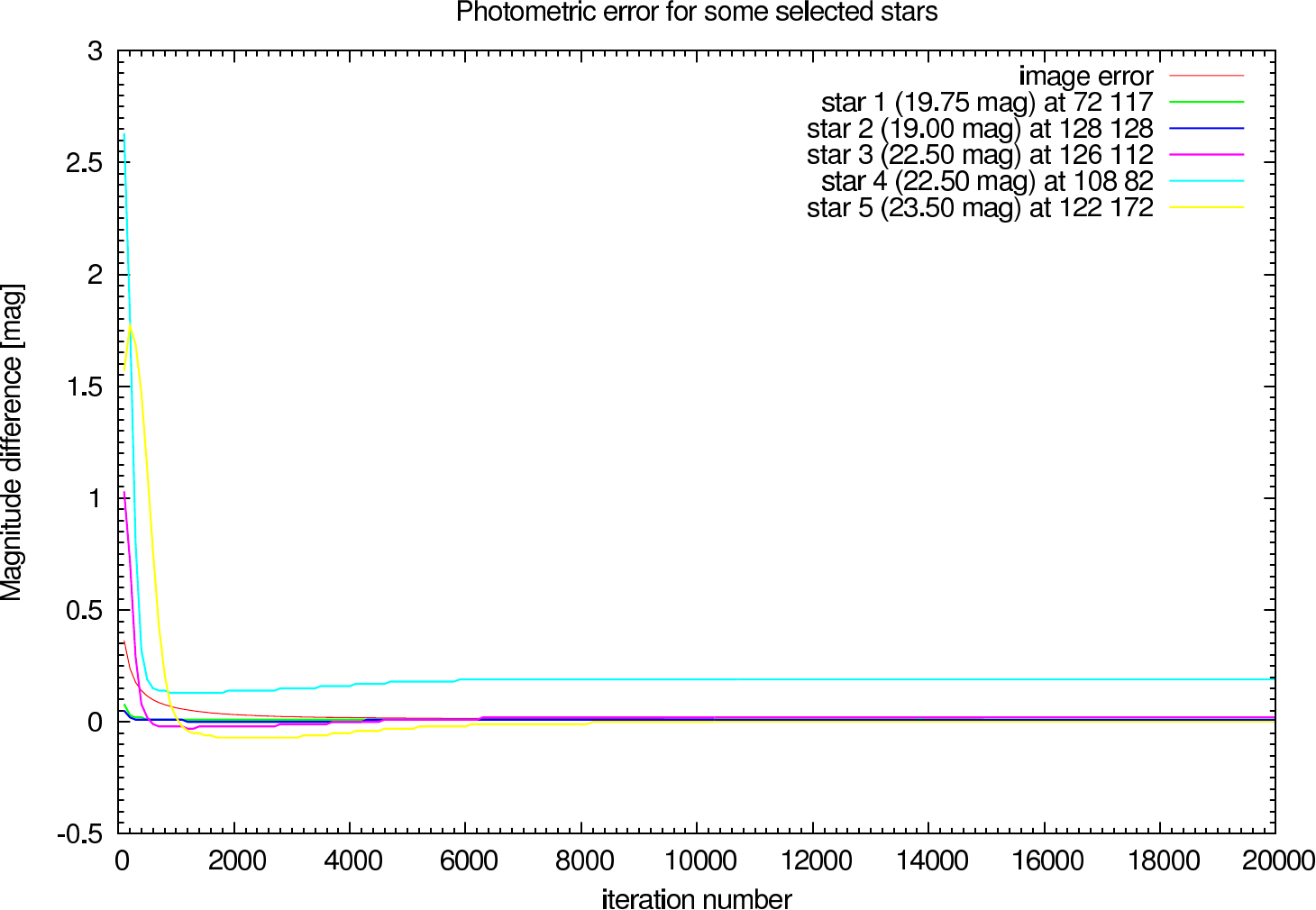 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |