Polychora
"As for the analogous figures in four or more dimensions, we can never fully comprehend
them by direct observation. In attempting to do so, however, we seem to peep though a
chink in the wall of our physical limitations, into a new world of dazzling
beauty."
H. S. M. Coxeter, in the preface of "Regular Polytopes".
The generalization of "polygon" in 2 dimensions and "polyhedron" in 3 dimensions to any
number of dimensions is a polytope. A 4-dimensional polytope is a
polychoron (plural
"polychora"). This is a finite region of 4-D Euclidean space* bound by at least 5
polyhedral 3-faces, or cells; it must
also have at least 5 vertices, 10 edges and 10 faces. These surface elements are,
together with the inner 4-D ``volume", part of the polychoron.
- Edges link two vertices; likewise, cells meet in pairs along their common faces.
- Just as each face is limited by an equal number of edges and vertices (which has to be
3 or larger), each edge is shared by an equal number of faces and cells (also 3 or
larger), specified by the edge's polygonal figure (henceforth
"edge figure"). The number of sides represents how many cells we have to go through to
complete a circuit around each edge. The lengths of the sides are the chords of the dihedral angles of
the cells.
- Just as each polyhedral cell is limited by at least 4 faces, 6 edges and 4 vertices,
at least 4 cells, 6 faces and 4 edges of polychoron A meet at each vertex P in a way
specified by a single polyhedral vertex figure. Its faces
correspond to vertex figures of the cells of A that touch P. Its edges correspond to faces
of A that touch P, their lengths are the chords of the inner angles of A's faces at P. Its
vertices and vertex figures correspond to the edges and edge figures of A at P.
In a regular polychoron all cells and vertex figures are regular. This implies that it is
isochoral: the cells are not only identical, but the polychoron looks the same seen
from all of them; this implies, for instance, that the polychoron has a well defined
centre and that all cells are equidistant from it. The same is true for the other types of
elements, i.e., the polychoron is also isogonal, isotoxal and isohedral. This also implies
that, analogously to what we have seen the polyhedra, each of the types of surface element
(four in this case) corresponds to a particular overall symmetry (in this case a
polyhedral symmetry) of the polychoron.
As we'll see, there are sixteen regular polychora: six are convex and ten are
non-convex. They were discovered, together with the higher-dimensional polytopes, by
Ludwig
Schläfli around 1850, but his manuscript on them was rejected, and only published
in 1901, six years after his death. In those 50 years, they were rediscovered by other
mathematicians, especially Edmund Hess.
If polychoron A is regular, its dual B is also regular. To each vertex of A corresponds a
cell in B, which is the dual of the vertex figure of A, and vice-versa. Each edge of A
goes through a perpendicular face of B, which is identical to that edge's figure, and
vice-versa. Two dual polychora must necessarily have the same symmetry.
* This is, again, a traditional definition that excludes honeycombs and apeirotopes.
Projections and sections
Projections:
Of course, we cannot build models of the polychora - the 3-D space we
inhabit does not allow it. The models below represent projections of polychora to our
3-dimensional Euclidean space. These cannot represent the inner 4-D volume of the
polychoron, only its ``surface'' elements. Their pictures - what you actually see in this
page - are projections of those models to two dimensions.
The best-known projections of polychora are perspective projections,
where vectors emanate from a single point at a finite distance. The pictures of the models
are of this type, where nearby 3-D objects are projected into the focal plane of the
camera. This type of projection can be used to portray 4-D objects into 3 dimensions, an
example of which are Schlegel diagrams. The most
common representation of any polychoron, the Tesseract represented as a Cube within a Cube
(see Fig. 5.1) is of this type.

Fig. 5.1: A perspective projection of the Tesseract in 3-D space, a 3-dimensional Schlegel
diagram, represented with the Zometool.
The projections below are not of this type. They are orthographic projections;
where the projection vectors are parallel to each other and perpendicular to the ``plane''
of the projection. In this regard they are more akin to Shadows produced by sunlight,
which (for this sort of purpose) are practically like parallel rays. Fig. 5.2 shows three
orthographic projections of three-dimensional figures (the Octahedron and the Cube) to 2-D
space. This will be used to illustrate many properties of these projections.
This type of projection is an example of an affine transformation,
meaning that a set of parallel lines in the polychoron are still parallel to each other in
its projection. This is not the case for the perspective projection in Fig. 5.1, where the
edges represented in yellow, which are parallel to each other in the Tesseract, are not
parallel in the projection.
There are infinite orthographic projections for any polytope, corresponding to an infinite
number of orientations of the polytope relative to the projection plane. In Fig. 5.2 and
below we show a few projections that can be represented with the Zometool system, i.e.,
that are "Zomable". If a polychoron has at least one such projection, we will likewise say
it is Zomable. All regular polychora are Zomable, below we show all their Zomable
projections. In addition, we show Zomable projections of a few closely related forms,
which are among the Archimedean
polychora, the 4-D analogues of the Archimedean solids.
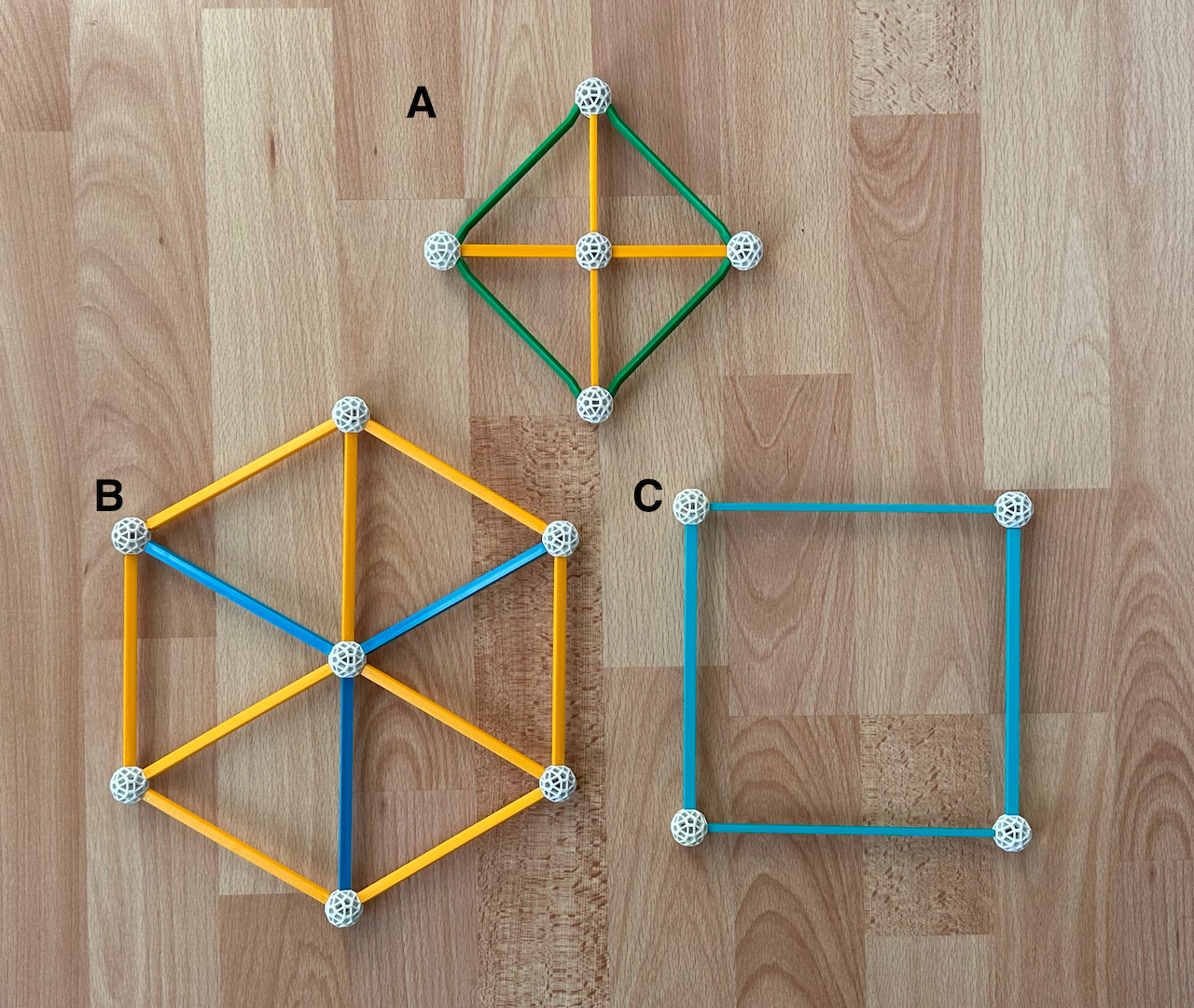
Fig. 5.2: Projections of the Octahedron (A) and Cube (B and C) into 2-dimensional space
represented with the Zometool. Projections A and B are "vertex-first", projection "C" is
face-first. Notice how projection B of the Cube looks larger than projection C.
The Zometool has two apparent disadvantages: First, it can only represent a small number
of projections. This is not much a problem, though, because the projections that can be
represented are almost always the most symmetric and beautiful. Second, it can represent
only the vertices (balls) and edges (struts) of the projection, the faces and cells must
be deduced from their vertices and edges. However, this feature is actually useful: since
all the projections below have a lot of important internal structure, representing the
faces (as in a paper model) would hide the internal structure of the projection. If a set
of polychora have different face and/or cell arrangements, but share an edge arrangement,
then their projections will share the same Zometool representation.
As we can see in Fig. 5.2, the central elements of a projection represent the elements of
the polytope that are ``closest'' and ``farthest'' from the plane of the projection. In
cases A and B, these are vertices, in case C the faces. In the projections below, these
are generally cells or vertices, although occasionally we show other types of projections.
The symmetry of these central elements reflects the symmetry of the axis along which the
polytope is being projected and determines the symmetry of the projection: as an example,
the projections of the Octahedron and Cube with Square symmetry (Fig. 5.2, A and C) result
from projecting the Octahedron and Cube along one of their axes of Square symmetry. An
important consequence is that, if the polytope and the central element have central
symmetry, then the ``near'' and ``far'' sides of the polytope coincide in the projection,
as in A and C. This is not the case for the vertex-first projection of the Cube in Fig.
5.2 (B): the central element (a vertex) has a Triangular vertex figure, which lacks
central symmetry. This implies that the "near" and "far" sides of the projection do not
coincide, this is why I represented the nearest and most distant edges in different
colours. This also means that the model represents two different projections, with
different sets of three edges closer to the viewer. The projections of polychora below
where this happens are marked by an asterisk (*); these are generally centred on
Tetrahedral cells or vertices with Tetrahedral vertex figures.
In any projections, most or all elements are necessarily distorted. For instance, the
edges of the Cube have three orthogonal directions that don't "fit" in a 2-D space. We can
deal with this in an infinite number of ways. In projection C in Fig. 5.2, two of the axes
are shown without distortion, this results in two Square faces: the projection is being
done through a 4-fold symmetry axis that passes through their centres. The third axis is
shortened to a point. In projection B, all three axes are presented identically, but all
are distorted; all Square faces are distorted into Rhombuses. However, in this projection,
the Triangular vertex figure of the central vertices is not distorted, because the
projection is being done along the 3-fold symmetry axis that passes through pairs of
opposite vertices.
One of the main reasons why the Zometool is a superb way to study the geometrical
properties of the polychora shown below is that it provides an easy way of seeing how
distorted an element is: their colour. Indeed, because orthographic projections are
affine, in a polytope with edges of identical lengths ℓ, a set S of parallel edges in
the polytope are still parallel and have identical length ℓ' in the projection, where
ℓ' = ℓ sin(ζ) and ζ is the angle between the edges of S and the
projection vector. A set of edges with identical lengths and directions can only be
represented, in a Zometool model, by struts of the same colour (and length and direction,
although the length can be divided between more than one strut because of intersections
with other edges).
This implies that each strut colour in the models below represents a specific value of sin
ζ that occurs in the projection. To calculate this, we use the Zometool strut lengths. For most models, the
longest struts are blue, in that case the values of ζ are:
| Colour | sin ζ | ζ |
| Blue | 1 | 90 |
| Red | √ (5 + √5) / 8) | 72 or 108 |
| Yellow | √ 3 / 2 | 60 or 120 |
| Smaller red | √(5 + √5) / 8 ) / φ = √2 √(5 − √5) / 4 | 36 or 144 |
| Points | 0 | 0 or 180 |
If the model includes Tetrahedra, Octahedra and Cuboctahedra, the longest struts are
green, in that case the angles are:
| Colour | sin ζ | ζ |
| Green | 1 | 90 |
| Blue | √ 2 / 2 | 45 or 135 |
| Yellow | √ 6 / 4 | 37.761 243... or 142.238 756... |
| Points | 0 | 0 or 180 |
It is therefore clear, in a model made with the Zometool, which elements are not
distorted. If one of these undistorted polyhedra is a cell (it can also be a section, see
below) then in 4-D it is the element closest or most distant from us, or lies directly
``under'' it; this corresponds in the projection to the central element or an object
concentric with it. For each instance of these undistorted elements, there will be many
more instances of the same element that are not in 3-D planes parallel to ours that will
appear distorted by the projection.
Sections:
Another way to understand a polytope is by cutting it with successive
"planes". The resulting sections are polytopes of a lower dimension. The succession
of sections of a polychoron gives us an idea of its 4-dimensional shape, in the same way a
set of two-dimensional sections describes a polyhedron, as in a 3-D printer.
For any polytope, there is an infinity of sections: as for the projections, we can orient
the polytope relative to relevant plane in an infinite number of ways. Below we will only
refer to symmetric sections starting either from a vertex or a cell (which will therefore
have the symmetry of the cell or vertex figure) that share vertices, edges or faces
with the polychoron. These we call vertex, edge or face sections.
If a polychoron has only Triangular faces, all vertex figures are necessarily
represented by the polychoron's edges; if these edges are in the same 3-D "plane" they
represent edge sections of the polychoron. If it has only Tetrahedral cells, all vertex
figures are necessarily represented by its faces; if these faces are in the same 3-D
plane they represent face sections of the polychoron.
If the cells of a regular polychoron A have central symmetry, then each cell has opposite
pairs of faces, which communicate with other identical cells. This means that those cells
form equatorial ``rings'' linked by a set of parallel faces. This implies, by duality,
that the vertex figures of the dual regular polychoron B also have central symmetry, and
that B's edges form equatorial Polygons, with vertices and edges corresponding to
the cells and faces of the equatorial cell ring of A. B's equatorial Polygons must form
equatorial polyhedra. The only polyhedra where all edges are part of equatorial
Polygons are the rectifications of regular polyhedra: even the Octahedron, the only
Platonic solid with equatorial Polygons, is a rectification (of the Tetrahedron).
Thus, all regular polychora with centrally symmetric vertex figures - and only those -
have equatorial polyhedra, and the latter are always rectifications of regular polyhedra.
Such equatorial polyhedra are edge sections of polychora by 3-D planes that pass through
their centres and are located either between opposite pairs of cells or vertices. Being
rectifications (which, apart from the Octahedron, have 2 types of faces), the equatorial
polyhedra have one type of face that does belong to the respective regular polychora
(which has only 1 type of face)*. The duals of polychora with equatorial polyhedra have
interconnected equatorial cell rings, with the same relative arrangements as the edges of
the rectified polyhedra.
* The exception is the 16-cell, its equatorial Octahedra have only one type of face,
Triangles, all of which are shared with the 16-cell. This allows the construction of a
semi-regular faceting of the 16-cell with the same face arrangement, the
Tesseractihemioctachoron, where 4 of the cells are the equatorial Octahedra and 8
cells are half of the Tetrahedra of the 16-cell.
Sections in projections:
Any edge or face section, having edges that belong to
the polychoron, will be represented in any projection of the polychoron that shows its
edges, like Zomable projections.
Any instances of the edge or face sections projected without distortion in the models
below will appear, as mentioned above, as green or blue polyhedra (according to the
model). In 4-D, these instances occur "under" the element that is being projected to the
center, in 3-D their projections will be concentric with the projection of the central
element. If an instance of the equatorial sections is projected without distortion, then
it is located (in 4-D) between the two diametrically opposed elements that appear, in 3-D,
superposed at the centre of the projection, its projection envelops the projection of the
whole polychoron.
Simple regular polychora
Before we move on, we need a clarification on the names. Some regular polychora have many
names - one is known as the 120-cell, Dodecaplex, Hyperdodecahedron, Polydodecahedron,
Hecatonicosachoron, Dodecacontachoron and Hecatonicosahedroid. The convention adopted here
is the same adopted by Wikipedia, which is to use the simpler names, for this example
"120-cell". This is consistent with the names of the regular polyhedra, which refer only
to the number of faces, not their type. This simple system works because the resulting
names are unambiguous. However, unlike the case of polyhedra and polygons, we don't use
Greek names: "120-cell" is much easier to understand, and shorter to write, than
"Hecatonicosachoron". There will be an exception to this: for the 8-cell we will use the
widely known term "Tesseract". This is also consistent with the polyhedral and polygonal
names, where the terms "Cube" and "Square" are at the same time technically precise (they
imply regularity) and do not obviously indicate the number of faces or edges.
***
The simplest regular polychoron, the 5-cell, is the 4-D analogue of the
Tetrahedron. It is bound by 5 Tetrahedral cells and has 5 vertices, with Tetrahedral
vertex figures. These cells have 5 × 4 = 20 Triangular faces, however, since each
face is shared by two cells the total number of faces is 10. The cells also have 5 ×
6 = 30 edges, but since the edges have Triangular figures (i.e., since each edge is shared
by three cells), there are only 10 edges. As mentioned above, this is the smallest number
of elements of these types any polychoron can have.
The symmetry of the numbers of elements (5-10-10-5) and the duality of the Tetrahedral
cells and Tetrahedral vertex figures imply that the 5-cell is, like the Tetrahedron,
self-dual. This property is shared by all their n-dimensional analogues, the Simplices.
The Tetrahedral projection of the 5-cell is shown in Fig. 5.3. Note how the outer
Tetrahedron, which is an undistorted cell, also represents the undistorted vertex
figure of the central vertex (this is also the case for any apex-first projections of
4-D pyramids, like the Cubic or Icosahedral pyramids, which
we'll meet later). To its left is a projection of the Rectified 5-cell.

Fig. 5.3: Projections of the 5-cell and its rectification, a semi-regular polychoron.
Left: A "vertex-first" and "cell-first" Tetrahedral projection of simplest regular
polychoron, the 5-cell (*).
Right: A Tetrahedral (thus, cell-centred) projection of the Rectified 5-cell (*).
We now use the 5-cell to illustrate the extension of the concept of rectification
(discussed previously for polygons and polyhedra) to polychora.
When rectifying the 5-cell, each of its 5 Tetrahedral cells is rectified into an
Octahedron. Each vertex of the 5-cell is replaced by its vertex figure, a Tetrahedron.
The number of vertices of the rectification is the same as the number of edges of the
5-cell, 10. In the 5-cell, each edge is shared by 3 Tetrahedral cells, this means that in
the Rectified
5-cell each vertex (located in the middle of the edge of the 5-cell) is touched by
three Octahedral rectifications of the previous cells, and by the two new Tetrahedral
cells, which relative to this vertex are opposite to each other. This means that the
vertex figure of the Rectified 5-cell is the Triangular prism. Since all
faces of the Rectified 5-cell are Triangular, these Triangular prisms are edge sections
lying under each of its 10 vertices, it is fun to find them in the model. This polychoron
is isotoxal, with each edge shared by one Tetrahedron and two Octahedra.
Since all its cells are regular, the Rectified 5-cell is one of the three semi-regular convex
polychora.
Both polychora in Fig. 5.3 have
Pentachoric symmetry. This has five axes of Tetrahedral symmetry, which go through
cells and opposite vertices of the 5-cell, and ten axes of Triangular prismatric symmetry,
which go through the edges and opposte faces of the 5-cell. All these lack central
symmetry, adding it we obtain the extended pentachoric symmetry. For more Zomable
projections of the 5-cell, see Fig. 7.8.
***
The 16-cell has four pairs
of vertices located along four orthogonal directions at the same distance from the centre.
It is the 4-D analogue of the Octahedron. It is bound by 16 Tetrahedral cells and has
Octahedral vertex figures. It has a Square edge figure. Following the logic used above
to calculate the number of elements of the 5-cell, we find it has 24 edges, and 32
Triangular faces. Its dual, the Tesseract, is the 4-D analogue of the
Cube. This is bound by 8 Cubic cells and has 16 vertices with Tetrahedral vertex
figures. It has 32 edges with Triangular figures and 24 Square faces.
These polychora share the Hexadecachoric symmetry. This has 4 axes of Octahedral symmetry, 8 axes of
Tetrahedral symmetry, 12 axes with Square prismatic symmetry and 16 axes of Triangular
prismatic symmetry.
In Fig. 5.4, we show different Octahedral projections of the 16-cell and Tesseract. For
more Zomable projections of the 16-cell, see Figs. 7.1a and b. For another projection of
the Tesseract, see Fig. 7.3.

Fig. 5.4: Octahedral projections of the 16-cell (left) and Tesseract (right).
On top are the vertex-first projections, bottom are the cell-first projections.
The cell-centred projection of the Tesseract (lower right) looks exactly like a Cube. In
this projection, the closest and most distant Cubes appear superposed. All others are
flattened to Squares by the projection. In this model, three of the axis directions are
preserved, and still look orthogonal, the fourth orthogonal axis is shortened to a point.
This projection is an analog to the Square projection of the Cube (C) in Fig. 5.2.
In the vertex-centred projection of the Tesseract (top right), the closest and most
distant vertices appear superposed at the centre. In this model, the four axes (and all
Square faces and all Cubic cells) are distorted, but are shown equally within 3-D space,
as indicated by all struts being the same colour and length. Note how each vertex is
connected to four struts. The equal treatment of the directions of the axes means that,
relative to the vertex closest to us in 4-D space (projected to the centre of the model),
these axes have an arrangement with Tetrahedral symmetry (see yellow struts within
Tetrahedron in Fig. 4.3b): for this central vertex, the vertex figure is not distorted.
Because this Tetrahedral vertex figure has no central symmetry, the near and far sides of
the projection do not coincide. The edges connecting to the opposite, most distant vertex
have the same directions, but from the opposite side of the central connector (these
connect to vertices of the Cube in Fig. 4.3b, but not to the Tetrahedron). For this
reason, this model represents two different projections of the Tesseract, which have
different sets of four edges closer to our 3-D ``plane''. Note how the model shows the
parallelism between a set of four yellow radial edge directions (Fig. 4.3a) and the yellow
edge directions of the envelope of the Figure, the Rhombic dodecahedron (Figs. 4.9,
4.10b). Notice too how the vertex-first projection of the Tesseract looks larger than its
cell-first projection, despite the shortened edges of the former! This projection is an
analog to the Hexagonal projection of the Cube (B) in Fig. 5.2.
Like all regular polychora with Tetrahedral cells, the edges and faces of the 16-cell
trace its vertex figure, the Octahedron, which in this case is an equatorial polyhedron
between pairs of opposite vertices. In the vertex-first projection (top left) we see one
undistorted Octahedron enveloping the two superposed opposite vertices at the centre, and
three flattened projections of Octahedra (Fig. 5.2, A) in three perpendicular planes
passing through the centre of the projection lying halfway between the outer vertices.
These equatorial Octahedra have themselves equatorial Polygons, Squares. They are
perpendicular to other equatorial Squares of the 16-cell, in the vertex-first projection
of the 16-cell, those projected as blue lines going through the centre are perpendicular
to the undistorted outer green Squares. These Squares correspond, in the dual polychoron
(the Tesseract), to equatorial rings of 4 Cubes joined with each other by 4 Square faces.
As for these equatorial figures, in the 16-cell the distance of a vertex to the centre is
√ 2 / 2 times the edge length (ℓ). This projection is an analog to the Square
projection of the Octahedron (B) in Fig. 5.2 (three such projections appear in its three
equators).
The cell-first projection of the 16-cell (lower left) is especially good for highlighting
its 8 vertices separately. Two opposite Tetrahedral cells superpose at the centre, in a
Stella Octangula configuration, one close to us, the other more distant. Thus, the
``near'' and ``far'' side of this projection are different. For this reason, this
projection represents two different projections of the 16-cell, each with one of the two
central Tetrahedra closer to our 3-D ``plane''.
We described above the meaning of duality between polychora. We now describe the meaning
of duality between projections. In Fig. 5.4, the vertex-first projection of the 16-cell is
the dual of the cell-first projection of the Tesseract; each cell of the former is centred
exactly on a vertex of the latter, and vice-versa. Equally, the cell-first projection of
the 16-cell is the dual of the vertex-first projection of the Tesseract. To the
undistorted green Squares of the vertex-first projection of the 16-cell correspond rings
of completely flattened Cubes in the cell-first projection of the Tesseract. Two dual
projections necessarily have the same symmetry.
Like the 5-cell, these regular polychora have analogues not only in 3-D, but also in any
n-dimensional Euclidean space. The Tesseract is the 4-D Hypercube, and the 16-cell is a 4-D cross polytope.
However, they have unique properties:
- The Tesseract is the only n-dimensional hypercube where the distance from the vertex
to the centre (given by √ n / 2 ℓ) is ℓ, i.e., that is radially
equilateral.
- The vertices of the 16-cell can be obtained by the alternating deletion of the
vertices of the Tesseract; this makes it the only cross polytope that is a member of the
aforementioned Demi-hypercubic family, and its
second and last regular member after the Tetrahedron.
This means that we can make a Compound of two 16-cells with the vertex arrangement of the
Tesseract; interestingly, the cell-first projection of the 16-cell in Fig. 5.4 can
represent such a compound! This implies, by duality, that its dual projection (the
vertex-first projection of the Tesseract) also represents a Compound of two Tesseracts. In
the projections of these compounds, the ``near'' and ``far'' sides are identical.
One of the consequences of the 16-cell being a Demi-tesseract is that if we start with a
Tesseract
honeycomb and do an alternating deletion of half of its vertices, we end up with a new
regular honeycomb
made of 16-cells: this is unique to 4 dimensions and the 16-cell is the only cross
polytope that can fill space! One of its projections would look like a filling of 3-D
space with the cell-first projections of the 16-cell, which would represent the 16-cells
concentric with the previous Tesseracts. The "new" 16-cells that fill the gaps between the
previous ones would be represented by vertex-first projections, which appear automatically
around the vertices where 6 blue struts meet.
How these properties of the 16-cell and Tesseract are related is discussed in more detail
below.
The 24-cell
Ultimately, the Rectified 5-cell owes its semi-regular status to a fact we mentioned when
discussing polyhedra: the rectification of a Tetrahedron is another regular polyhedron,
the Octahedron. This means that, when we rectify any regular polychoron with Tetrahedral
cells, we obtain a semi-regular polychoron bound by Octahedral cells and cells identical
to the former's (regular) vertex figure. The new vertex figures are equilateral prisms,
with a "base" given by the edge figure of the regular polychoron that was rectified.
Things are even more interesting when we rectify the 16-cell. Doing this, we create a
polychoron where 16 Octahedral cells result from rectifying the Tetrahedra of the 16-cell
and where 8 new Octahedral cells are the vertex figures of the 16-cell. The edge figure of
the 16-cell is the Square, this implies that the vertex figure of the Rectified 16-cell is
the Square prism, i.e., the Cube. The regularity of cells and vertex figures means that
this rectification is regular: the 24-cell.
In Fig. 5.5a, we show the cell-first projection of the 24-cell. This results from
rectifying either the cell-first or the vertex-first projections of the 16-cell in Fig.
5.4.
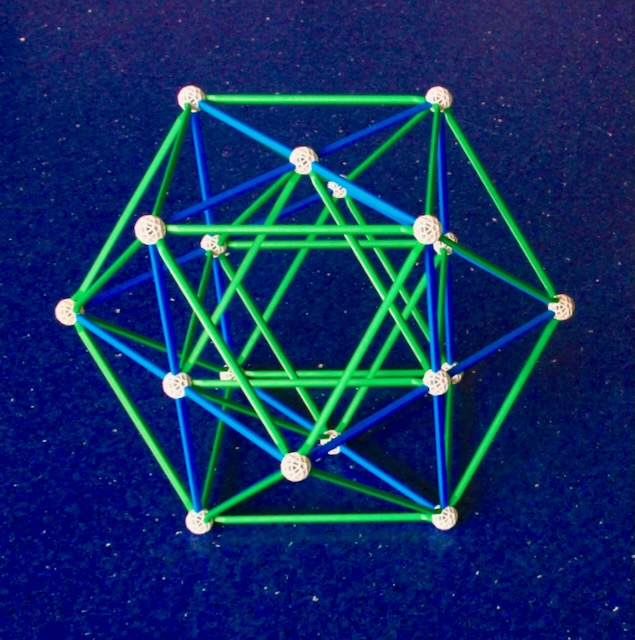
Fig. 5.5a: The cell-first projection of the 24-cell.
Because it is a rectification of the 16-cell, the number of its vertices has to be the
same as the number of edges of the 16-cell, also 24. The number of edges (which have
Triangular figures) and Triangular faces is 96. This and the fact that the cells and
vertex figures are duals implies that the 24-cell is self-dual. In all Euclidean
n-dimensional spaces, this is the only regular convex polytope with this characteristic
that is not a Simplex or a Polygon.
The 24-cell has its own unique Icositetrachoric symmetry, which has 24 axes of Octahedral
symmetry: twelve of these go through pairs of opposite vertices, and another twelve (which
can be thought of as the dual axes) go through opposite pairs of cells. In a dual 24-cell,
these axes change roles. It also has 96 axes of Triangular prismatic symmetry, 48 go
through pairs of opposite faces, and 48 dual axes go through pairs of opposite edges. If
the two sets of symmetry axes have identical elements, the resulting object would have
the extended Icositetrachoric symmetry.
The 24-cell and its symmetry have no analogs in any other n-dimensional space, i.e., the
24-cell and its symmetry are clearly exceptional objects! We will
now find why.
The previous way of building the 24-cell (by rectifying the 16-cell) is known as Cesàro's
construction (Coxeter, 1973); this is the 4-D equivalent of obtaining a Cuboctahedron from
an Octahedron by rectification. The "dual" construction of the 24-cell (Gosset's construction) is
equivalent to the construction of a Rhombic dodecahedron from two Cubes mentioned above. This construction
illustrates especially well why the 24-cell is unique to 4 dimensions.
Step 1: Divide Tesseract A into 8 Cubic pyramids (these can be
represented by the model in Fig. 4.3a). Their 4-D volume is limited by a Cubic "base" (one
of the previous cells of the Tesseract) and by 6 Square pyramids, the "sides", the apex
lies 1/2 ℓ above the base, the distance of a Cubic cell to the centre of its
Tesseract.
Step 2: Separate these Cubic pyramids and "glue" their Cubic bases to the Cubic
cells of a second identical Tesseract, B, making those cells - and all Square faces -
disappear. Square pyramids from two neighbouring Cubic pyramids now contact each other
through what were their Square bases, thus forming 24 Octahedra - the cells of the
24-cell.
As shown by the construction of the Rhombic dodecahedron from Cubes, similar constructions
can be made in any dimensional space. The difference in 4 dimensions is that Tesseracts
are, as mentioned above, radially equilateral. Therefore, the Cubic pyramids and their
Square pyramid "sides" used in the previous steps are also equilateral, a necessary
pre-condition for building Octahedra.
To the 16 vertices of Tesseract B, all at distance ℓ from the centre, 8 new ones were
added: the apices of the Cubic pyramids, which lie "above" each Cubic cell of B, also at
distance ℓ from its centre (see Fig. 5.5b, where Tesseract B appears in cell-first
projection, in blue). Thus, the 24-cell is, like the Tesseract, radially equilateral.

Fig. 5.5b: The vertex-first projection of the 24-cell, known as its "pyritohedric"
projection. This is the dual of the projection in Fig. 5.5a. The two superposed central
vertices appear ``above'' two superposed undistorted Cubic edge sections, in blue. The
outermost vertices appear above Cubes flattened by the projection.
Since each of the 8 new pyramidal apices (touched only by yellow struts in Fig. 5.5b)
hangs over a cell of Tesseract B, they have the vertex arrangement of the dual of the
Tesseract, the 16-cell. Thus, the 24-cell has the vertices of a dual compound, the
Tesseract and the 16-cell. Furthermore, as we've seen above, we can divide the vertices of
any Tesseract into those of another two 16-cells, therefore the vertices of the 24-cell
can be decomposed into three sets of vertices of the 16-cell. As we will see, a set of
three 16-cells with the vertices of the 24-cell is a regular polychoron compound (see Figs. 7.2a, b and c).
Since the 24-cell has Triangular faces, its vertex figure (the Cube) is necessarily an
edge section, with one such Cube located under each vertex of the 24-cell (see Fig. 5.5b).
Since these vertices have the same arrangement as the vertices of the Compound of three
16-cells, those Cubic sections must be arranged as the cells of the dual compound, which
necessarily consists of three Tesseracts. This includes Tesseract B plus two others that
appear in Fig. 5.5b in vertex-first projection (see Fig. 5.4).
As suggested by their derivations, the Cuboctahedron and Rhombic dodecahedron are the
closest polyhedral analogues to the 24-cell:
- The Cuboctahedron in green envelops the projection of the 24-cell in Fig. 5.5a, it is
therefore the instance of its equatorial polyhedron located halfway between the two
opposite Octahedral cells at the centre. It results from the application of
Cesàro's construction (rectification) to the Octahedral envelope of the
vertex-first projection of the 16-cell in Fig. 5.4. Since the 24-cell has 12 pairs of
opposite cells, there are 12 instances of equatorial Cuboctahedra; which are perpendicular
to the twelve axes of Octahedral symmetry that go through those cells. All of their
projections are visible in all models of the 24-cell.
Since the 24-cell is radially equilateral, its equatorial polyhedron, the Cuboctahedron,
must also be so. We have already seen that this is the case, because the latter's
equatorial Polygon, the Hexagon, is also radially equilateral. The Hexagon is the only
regular convex polytope that shares this property with the Tesseract and 24-cell.
- The Rhombic dodecahedron is the envelope of the vertex-first projection of the 24-cell
(Fig. 5.5b) because it results from the application of the Gosset construction to the Cubic
envelope of the cell-first projection of the Tesseract in Fig. 5.4.
The existence of equatorial polyhedra and Polygons is a consequence of the central
symmetry of the vertex figure of the 24-cell. The self-duality of the 24-cell means that
the cells must also have central symmetry, which means that the 24-cell also has
equatorial cell rings: it is the only regular convex polychoron with both, and they are
dual to each other. In Fig. 5.5a, we see one of these rings as a small ``tunnel'' at the
centre of the projection consisting of 6 Octahedra, we also see an outer Hexagon that is
perpendicular to that ring. In the projection in Fig. 5.5b of the dual 24-cell, the
central cell rings are replaced by their duals, radial line-like Hexagons (distorted in
this way by the projection) and the outer perpendicular Hexagons are replaced by their
duals, rings of 6 Octahedral cells that are completely flattened by the projection.
Like the Rhombic dodecahedron, the 24-cell can fill space. To see this, we apply the
process used above to
transform a Cubic honeycomb into a Rhombic dodecahedron honeycomb to a Tesseractic honeycomb:
First, we divide the latter into two alternating sets of Tesseracts. Second, we divide all
Tesseracts in one of the sets into Cubic pyramids. Third, we attach their Cubic bases to
the Cubic cells of their neighbouring Tesseracts, thus making 24-cells via Gosset's
construction above. This is the regular 24-cell honeycomb.
The dual of the latter honeycomb must also be regular; it is in fact the 16-cell honeycomb
mentioned above! The reason for this is simple: if we start with two dual Tesseractic
honeycombs A and B, then the alternate removal of half of all Tesseracts in A (to make
24-cells) will cause the alternate removal of half of all vertices in B. The addition of
vertices in A (at the centres of alternating sets of Tesseracts) marks the centres of
"new" 16-cells in B. B thus becomes the 16-cell honeycomb mentioned above.
Thus, the fact that the Tesseract is radially equilateral leads to the existence of the of
the 24-cell and is the ultimate reason why 4-D space is, together with the 2-D Euclidean
space, the only n-dimensional Euclidean space with three regular honeycombs. All others
have only their respective Hypercubic honeycombs!
These unique honeycombs have an interesting property demonstrated only recently: if we
replace the 24-cells of the 24-cell honeycomb (or the vertices of the 16-cell honeycomb)
with concentric 3-spheres, the resulting arrangement is
the densest possible regular sphere packing in 4 dimensions,
where each sphere kisses 24 others.
The 600-cell and the 120-cell
We will now describe a construction of the more complex polychora based on the 24-cell,
also known as Gosset's construction (see Coxeter 1973).
Step 1: Rectify the 24-cell, obtaining the Rectified 24-cell (Fig. 5.6).
For each of the 24 Octahedra of the 24-cell the latter has one Cuboctahedron (the
rectification of the Octahedron). For each of the 24 vertices of the 24-cell, the
Rectified 24-cell has a Cube (the vertex figure of the 24-cell). This polychoron has
96 vertices, one for each edge of the 24-cell.
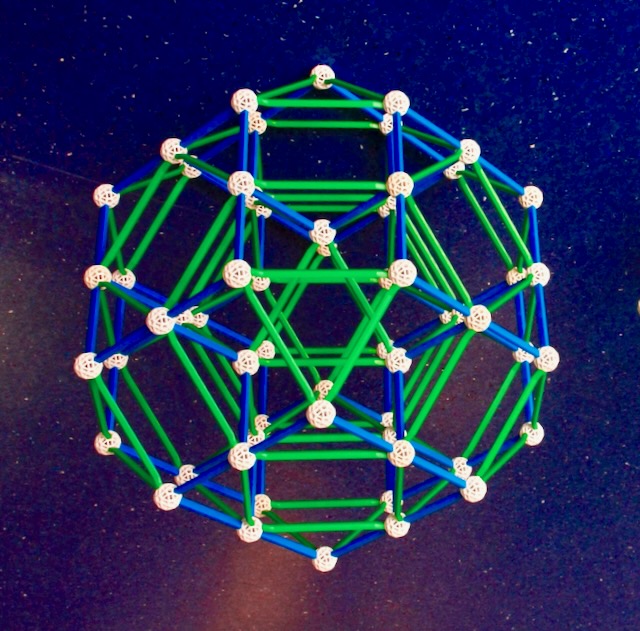
Fig. 5.6: A cuboctahedral-cell-first projection of an Archimedean polychoron, the
Rectified 24-cell. All projections of the Cube and Cuboctahedron in this model are
already present in the model of the 24-cell in Fig. 5.5a.
How to build: Have a look at the Eusebeia page on the Rectified 24-cell.
For this projection, see the part on the "Cantellated 16-cell".
Step 2: Diagonally bisect all of its Squares. If the diagonals are chosen
correctly, then each of the 12 vertices of the Cuboctahedral cells has five edges and five
triangular faces converging on it, i.e., it has been transformed into an irregular
icosahedron (Fig. 5.7). The Cubic cells of the Rectified 24-cell have been transformed
into sets of five Tetrahedra, with only the central one being regular.

Fig. 5.7: Being a rectification of the Octahedron or Cube, the Cuboctahedron (in green,
see also Fig. 3.4) has 12 vertices, the number of edges of the Cube and Octahedron. This
is the same number of vertices as the Icosahedron. That is why their duals are both
dodecahedra, respectively the Rhombic dodecahedron (Fig. 3.4) and the Dodecahedron (Fig.
3.1).
The reason for the identical number of vertices is that if we add new edges along the
diagonals of the Square faces of the Cuboctahedron as shown here (in blue), it becomes an
irregular Icosahedron, with 5 edges and 5 triangles converging on each of its vertices. By
shortening those diagonals to the size of the other edges, we transform the irregular
icosahedron into a regular one. None of these transformations changed the number of
vertices.
The blue diagonals break the Octahedral symmetry of the Cuboctahedron, this model has
pyritohedric symmetry.
Step 3: Shorten these Square diagonals until they have the same length as the other
edges. This is possible because of the very peculiar kinematics of the
Cuboctahedron. This generates one regular Icosahedron for each of the previous 24
irregular icosahedra, and 24 clusters of five Tetrahedra, 120 in total. The resultant
polychoron is the Snub
24-cell (Fig. 5.8).

Fig. 5.8: This is an icosahedral-cell-first projection of an Archimedean polychoron, the
Snub 24-cell.
Like the model in Fig. 5.7, this model has pyritohedric symmetry.
How to build: Have a look at the Eusebeia page on the Snub 24-cell.
Also recommended is David Richter's page on
the 24-cell and its snub.
The second and third steps preserved the number of vertices of the Rectified 24-cell, 96,
all of them are still identical to each other, the vertex figure is a Johnson solid, the tri-diminished
icosahedron. Because all faces are Triangles, this vertex figure is an edge section of
the Snub 24-cell, with one tri-diminished Icosahedron appearing (in 4-D) under each
vertex.
Because it is isohedral and its cells are Uniform, the Snub 24-cell is a Uniform
polychoron. Because all its cells are regular, it is also semi-regular. However, and
unlike all other polychora in this page, this is neither regular nor derived from a
regular polychoron by rectification; it is also not isotoxal. Although it is derived from
the symmetry of the 24-cell, it is less symmetric, having the ionic diminished Icositetrachoric symmetry.
Step 4: Glue an equilateral Icosahedral pyramid
(consisting of an Icosahedral "base" and 20 regular Tetrahedra as "sides", see Fig. 5.9)
by its base to each of the 24 Icosahedral cells of the Snub 24-cell.

Fig. 5.9: Icosahedral projection of the Icosahedral pyramid, a non-uniform polychoron.
This can be seen as an "apex-first" projection, but also as a "base-first" projection,
where the base is the outer Icosahedron. This pyramid can be equilateral (in 4-D) because
the Icosahedron's circumradius (red struts) is slightly smaller than its edge length (blue
struts).
The Icosahedral cells disappear. The 120 Tetrahedra of the Snub 24-cell are now joined by
the 24 × 20 Tetrahedra = 480 Tetrahedra of the new 4-D "Pyramids", making a total of
600 Tetrahedral cells. Together with the previous 96 vertices of the Snub 24-cell, the new
24 pyramidal apices add to a total of 120 vertices. The former's vertex figures are still
identical to each other; in fact they have all become regular: 20 Tetrahedra now meet at
each vertex, which means that the vertex figure is an Icosahedron. This is also the case
for the 24 new pyramidal apices!
Since all cells and vertex figures are regular, we have built a new regular polychoron,
the 600-cell! It has 1200
Triangular faces and 720 edges with Pentagonal figures. This is the 4-D analogue of its
vertex figure, the Icosahedron; its symmetry, known as the Hexacosichoric symmetry, is the 4-D analogue of the
Icosahedral symmetry: it has 60 axes of Icosahedral symmetry, which go through opposite
vertices of the 600-cell, and 300 axes of Tetrahedral symmetry, which go through the
centres of opposite Tetrahedral cells. It also has 360 axes of Pentagonal prismatic
symmetry, which go through opposite edges, and 600 axes of Triangular prismatic symmetry,
which go through opposite faces. The Icosahedral projection of the 600-cell is shown in
Fig. 5.10; this is necessarily a "vertex-first" projection.

Fig. 5.10: The Icosahedral projection of the 600-cell.
How to build: see instructions in David Richter's list of
projects with the Zometool.
By studying the model, we can make a Table with all the vertex arrangements (vertex
sections) starting from a vertex and ending in the opposite vertex. All of these are
perpendicular to one of the 60 axes of Icosahedral symmetry. The projection in Fig. 5.10
is made along one of these Icosahedral symmetry axes, which passes through the two
opposite vertices, which are projected to the centre. The vertex arrangements
perpendicular to this particular axis are projected without distortion around the central
vertex of the projection. This list will be important for understanding much of what
follows. For lists of vertex sections centred on vertices and cells for all convex
regular polychora see Table V of Coxeter (1973).
|
| Section | N. of vertices | Vertex arrangement | Note |
|
| 0 | 1 | Point | The vertex closest to us, at the centre of the projection. |
| 1 | 12 | Icosahedron | This matches the vertex figure of the 600-cell. |
| 2 | 20 | Dodecahedron | These vertices are a reflection of the central vertex through each of the 20 faces of the previous Icosahedron. |
| 3 | 12 | Icosahedron | These vertices are a central reflection of the central vertex through each vertex of the previous Icosahedron.
They appear in the projection as a φ times larger arrangement than the inner Icosahedron.
They are the outermost vertices with that arrangement. |
| 4 | 30 | Icosidodecahedron | This is the outermost set of vertices of the model, representing the equatorial polyhedron,
the section of the 600-cell through its middle between opposite vertices.
Its Triangular faces are a central reflection (via the vertices of the previous Dodecahedral section)
of the Triangular faces of the inner Icosahedral section.
|
| After this, the sections are a repeat of the sections above in reverse order, they are closer to the most distant vertex. |
| 5 | 12 | Icosahedron | These 12 vertices are superposed to those of section 3. |
| 6 | 20 | Dodecahedron | These 20 vertices are superposed to those of section 2. |
| 7 | 12 | Icosahedron | These 12 vertices are superposed to those of section 1. |
| 8 | 1 | Point | Most distant vertex from us. Appears superposed to that of section 0. |
| Total: | 120 | - | - |
|
Table 3: Vertex sections of the 600-cell, starting from a vertex. All have
the symmetry of the vertex figure of the 600-cell.
In the model of the 600-cell in Fig. 5.10 we see undistorted instances of edge
arrangements (in blue) with most vertex arrangements listed in Table 3, which means that
they represent edge sections of the 600-cell:
- As mentioned above, for regular polychora with Tetrahedral cells, their vertex figures
- in this case Icosahedra - are inevitably highlighted by their faces. This means that
sections 1 and 7 in Table 3 are face sections of the 600-cell.
- The edges of the Icosahedral sections are shared by Great dodecahedral sections, which
have the Pentagonal sections of the Icosahedron as faces. These are edge sections of the
600-cell.
- We also see that the vertices of the Dodecahedral sections of the 600-cell - numbers 2
and 6 in Table 3 - are also linked by edges of the 600-cell. This means that they are edge
sections of the 600-cell.
- The vertices of the equatorial Icosidodecahedral sections (section 4 in Table 3) are
also linked by the edges of the 600-cell; its Triangular faces are also those of the
600-cell, i.e., this is partly a face section. The equatorial polygon of the 600-cell is
thus the same as for the Icosidodecahedron, the Decagon.
Thus, the edges of the 600-cell - where each vertex is connected to the closest vertex in
the arrangement (section 1) - represent edge sections with the vertex arrangements 1,2,4,6
and 7 in Table 3, with 0 and 8 being represented by the connectors themselves.
For each of the 120 identical vertices of the 600-cell, there are singular instances of
these three regular edge sections under each vertex. There are also 60 instances of the
equatorial Icosidodecahedra, each lying halfway between each pair of opposed vertices. In
the projection, we can see projections of all these instances! We also see that, for each
equatorial Decagon, there is another perpendicular Decagon: for instance, for each of the
6 undistorted Decagons in blue, there is a perpendicular Decagon that is distorted to a
red line going through the centre. The latter are aligned with the six axes of 5-fold
symmetry of the projection.
The fact that the edges of the 600-cell highlight equatorial Icosidodecahedra and Decagons
implies that, as for those two figures, R0 = φ ℓ.
Challenge to the reader: After building the model of the 600-cell, locate the
perfectly flat projections of the Icosahedron, Dodecahedron and Icosidodecahedron under
each vertex of the outer blue Icosidodecahedron.
The Icosahedral face sections share the Triangular faces of the Tetrahedral cells, the
Great dodecahedral edge sections share the Pentagonal faces of the Dodecahedral edge
sections. All these Triangular and Pentagonal faces are shared with the equatorial
Icosidodecahedral sections. As we'll see next, these
regular edge and face sections are cells of three regular facetings of the 600-cell that
have the same edges, and in some cases the same faces. They are analogous to the Great
dodecahedron, which has the edges of the Icosahedron and the latter's Pentagonal edge
sections as faces.
***
The dual of the 600-cell is necessarily a regular polychoron sharing its symmetry, 600
vertices with Tetrahedral vertex figures that appear in pairs along the 300 axes of
Tetrahedral symmetry, 1200 edges with Triangular figures (in pairs along the 600 axes of
Triangular prismatic symmetry), 720 Pentagonal faces (which appear in pairs along the 360
axes of Pentagonal prismatic symmetry) and 120 Dodecahedral cells, which appear in pairs
along the 60 axes of Icosahedral symmetry: the 120-cell. This is the 4-D equivalent of
its cell, the Dodecahedron. Fig. 5.11 shows a model of its Icosahedral projection. Two of
its Dodecahedral cells appear undistorted at the centre of projection: an Icosahedral
projection of the 120-cell is necessarily a cell-first projection.

Fig. 5.11: This is the Icosahedral projection of the 120-cell. This projection is the dual
of the projection of the 600-cell in Fig. 5.10.
How to build: see instructions here. The model in the
figure is φ times larger than the set sold by the Zometool company as the hyperdo.
If you pay attention to the model, you will see that all of these projections of
Dodecahedral cells can already be seen as the Dodecahedral edge sections in the model of
the 600-cell! This situation is similar to that of the Icosahedron, which contains all
faces of the Dodecahedron as Pentagonal sections.
Apart from the cells, we see no additional edge sections, as there are no Triangular
faces, however, as we will see, there are plenty of vertex sections, either centred on
the vertices or the cells. There are no equatorial polyhedra because the vertex figure of
the 120-cell (the Tetrahedron) has no central symmetry. However, for each equatorial
Decagon of the 600-cell, we see in the 120-cell a dual ring of 10 Dodecahedra joined with
each other by 10 parallel Pentagonal faces. Some of these rings are the central tunnels we
see in this projection; these are the duals of the Decagons projected as red lines going
through the centre of the projection of the 600-cell in Fig. 5.10. The duals of the
perpendicular Decagons of the 600-cell (which in that projection are undistorted and
appear in blue) are in this projection the outer rings of ten perfectly flattened
Dodecahedra.
With the 120-cell, the list of regular convex polychora is complete. This will be shown in
detail next in our enumeration of all regular polychora in the next page.
Paulo's polytope site / Next:
The regular star polychora.












