Archimedean polytopes

Archimedean solids

 Apart from the Platonic solids, there are many other convex uniform polyhedra, which include the two infinite classes of Prisms and Antiprisms, plus the 13 Archimedean solids. In Fig. A.1, I show paper models of the latter, which I made in the late 1990's. Their duals are known as the Catalan solids, the latter include the aforementioned Rhombic dodecahedron and Rhombic triacontahedron.


Fig. A.1: The Archimedean solids.


In the front row is the Truncated tetrahedron.

In the second row, from left to right, is the Cuboctahedron, the Truncated octahedron, the Truncated cube, the Rhombicuboctahedron, the Truncated cuboctahedron (also known as the Omnitruncated cube or octahedron) and the Snub cube.

In the back row, from left to right, is the Icosidodecahedron, the Truncated icosahedron, the Truncated dodecahedron, the Rhombicosidodecahedron, the Truncated icosidodecahedron (also known as the Omnitruncated dodecahedron/icosahedron) and the Snub dodecahedron.

The front row has objects with Tetrahedral symmetry. The second row has objects with Octahedral symmetry. The last row has objects with Icosahedral symmetry. However, the Snub cube and the Snub dodecahedron lack mirror symmetry - they are different from their mirror images. Their symmetries are, respectively, the chiral ochahedral and the chiral icosahedral symmetries.

These solids are illustrative examples of different types of the Wythoff construction. This construction is based on the idea of symmetry as a reflection. In an object with, for instance, bilateral symmetry, the left and right sides are identical, but appear as if reflected in a mirror. Thus, in this case, we could start with the right side of the object and obtain the left side by reflecting it in a mirror, generating the whole symmetric object.

Thus, any highly symmetric figure - like all regular polytopes - can be buit from reflections in a particular set of mirrors: a kaleidoscope. For symmetric polyhedra, these mirrors are the edges of a spherical Schwarz triangle (which can tile of a spherical surface), which are the fundamental domain of a 3-D point symmetry group.

In Fig. A.1, we meet several types of Wythoff construction. The regular polyhedra and their rectifications (the latter are shown in the first column on the left in Fig. A.1) share the same type of Wythoff construction: Their vertices are reflections of one of the three vertices of the Schwarz triangle. This means that for each pair of dual regular polyhedra (i.e., for each type of symmetry) there is only one rectified form. A consequence of this type of Wythoff construction is that all regular polyhedra and rectifications are isotoxal, i.e., all edges are identical.

The difference regarding the rectification is that the vertex being reflected is at the right angle of the Schwarz triangle, thus at the intersection of two perpendicular mirrors. Thus, any edge touching that vertex is reflected by those mirrors, generating a rectangular vertex figure. This implies that all edges, apart from being identical, separate two types of faces. Furthermore, as we've seen already in the polyhedron page, the central symmetry of these vertex figures implies that these polyhedra have equatorial Polygons.

Another type of Wythoffian construnction is the truncation. Here, the vertices of a regular polyhedron are cut, as in a rectification, but not so deeply that the cuts touch each other, instead leaving a length of edge between the previous faces that is identical to the edges of the cuts. For each symmetry, there are three truncated forms (columns 2, 3 and 4 in Fig. 1), where the vertices result from reflecting points in the edges of the Schwarz triangle, i.e., located in one of the mirrors. All their vertex figures will, because of this, have bilateral symmetry.

A third type of Wythoffian construnction is the omnitruncation (column 5 in Fig. A.1), where the vertices result from reflecting points inside the Schwarz triangle. There is only one such polyhedron for each type of symmetry. This means that in a polyhedron generated this way, the number of vertices will be, for a particular symmetry, the same as the number of Schwarz triangles that tile the spherical surface, which is the order of the associated symmetry group. The Omnitruncated octahedron/cube has 48 vertices and the Omnitruncated icosahedron/dodecahedron has 120 vertices (more about the Omnitruncated tetrahedron next). The vertex figure will be close to the dual of the Schwarz triangle.

Finally, there is a particular type of transformation that produces one snub form for each symmetry. This works by alternate deletion of Schwarz triangles.

***

In Fig. A.1 we only show one polyhedron derived from the Tetrahedral symmetry, the Truncated tetrahedron. The reason for this is that when we apply the different Wythoff constructions to the Tetrahedral symmetry, the resulting forms are, with the exception of the Truncated tetrahedron, redundant with polyhedra derived from other symmetries. As mentioned in the polyhedron page, the Rectified tetrahedron is the Octahedron. In addition, the Rhombitetrahedron is the Cuboctahedron; the Omnitruncated tetrahedron is the Truncated octahedron (which, like all omnitruncated simplexes, is a permutohedron, all of which can fill the Euclidean space they are embedded in); this has 24 vertices, which is the order of the Tetrahedral symmetry. The Snub tetrahedron is the Icosahedron.

Therefore, many polyhedra have multiple Wythoff constructions, i.e., they can be derived from different symmetries. The overlap in forms between the Tetrahedral and Octahedral symmetries is not surprising as the Tetrahedron is the demi-cube (the 3-dimensional version of a Demihypercube, obtained by alternate deletion of vertices of Hypercubes).


Fig. A.2: The Platonic (three polyhedra on the left) and Archimedean (three polyhedra on the right) solids with Tetrahedral and Octahedral symmetries that can be built with Zometool. The polyhedra in green can be derived from the Tetrahedral symmetry.


Finally, one word on which of these polyhedra are Zomable: Indeed, of the polyhedra derived from Octahedral symmetry, only those that can also be derived from Tetrahedral symmetry - and the Cube - are Zomable (see Fig. A.2)! This will have some interesting implications below.

Just like we can apply the concept of the Wythoff construction to polyhedra, we can also apply it to the regular tilings of 2-D Euclidean space, which are the flat analogs of the polyhedral surface. Doing this, we obtain all the Archimedean tilings of 2-D Euclidean space, with the exception of the elongated triangular tiling, which is non-Wythoffian. These tilings are of practical interest for fields like architecture, design and engineering.

Finally, it should be noted that if we lift the condition of convexity, several other types of Uniform polyhedra become possible: an infinite family of Star prisms and antiprisms, and a finite family of ``Star Archimedeans'', which include the regular star polyhedra (Fig. 3.5a), their rectifications (Fig. 3.6a) and the ditrigonal polyhedra (Fig. 3.7) as special cases. Most of these are obtained by the Wythoff construction acting on Schwarz triangles with non-integer indices, with one exception, the Great dirhombicosidodecahedron.

Archimedean polychora

 The uniform convex polychora include, in addition to the regular convex polychora, several types of 4-D prisms and 47 non-prismatic polychora. By analogy with the Archimedean solids, I will refer to the latter as the "Archimedean" polychora.

Like the Archimedean solids, these Archimedean polychora illustrate different types of Wythoff construction. The mirrors of the underlying Kaleidoscope are the faces of spherical Goursat tetrahedra (which tile the 3-sphere), which are the fundamental domains of a 4-D point symmetry group. All but one of the 47 Archimedean polychora can be built in this way; the exception is discussed below.

All Zometool models below have been disassembled. I have not kept them for lack of Zometool parts, but also because the models of the regular polytopes and their regular compounds already take a lot of space in my office!

Rectifications:

As for the polyhedra, the regular polychora and their rectifications also share the same type of Wythoff construction: their vertices are reflections of one of the four vertices of the Goursat tetrahedron. For most symmetries, this implies that for each dual pair of dual regular polychora, there are two rectified polychora. As in the case of the rectifications among the Archimedean solids, all of these forms are isotoxal.

Also, as for the regular counterparts, all rectifications are Zomable. In the page on the regular convex polychora we have already seen models of the Rectified 5-cell, the Rectified 16-cell (which is regular, the 24-cell) and the Rectified 24-cell. Below we show the rectifications of the three remaining convex regular polychora.

We first present two projections of the Rectified tesseract. The 8 Cubes of the tesseract were rectified, becoming Cuboctahedra. Under the 16 vertices of the Tesseract new Tetrahedra appeared. Each edge is shared by one Tetrahedron and two Cuboctahedra.


Fig. A.3a: Projection of the Rectified tesseract, centred on a Cuboctahedral cell. This projection is the rectification of the cell-first projection of the Tesseract.


Fig. A.3b: On the right is the projection of the Rectified tesseract(*) centered on two opposite Tetrahedral cells. This is the rectification of the vertex-first projection of the Tesseract(*) on the left. In particular, the Yellow rhombuses, which are represented by yellow struts, get rectified into Yellow rectangles, which have green and blue struts (see Fig. 2.5a). Unlike the projection of the Rectified tesseract in Fig. 3a, but similarly to what happens with the vertex-first projection of the Tesseract, the central element lacks central symmetry, which means that the "near" and "far" sides of the projection do not coincide (hence the asterisks). For that reason, the opposite Tetrahedra supperpose in a Stella Octangula configuration. This means that this model represents, in fact, two different projections, each with one of the two Tetrahedra at the center closer to us.


In the page on the regular convex polychora, we have seen two semi-regular convex polychora (which, apart from being Uniform, have only regular cells, in these cases of two distinct types): the Rectified 5-cell and the Snub 24-cell. There is a third and last semi-regular convex polychoron, the Rectified 600-cell. As in the case of the Rectified 5-cell, this results from rectifying a regular convex polychoron with Tetrahedral cells: the 600 Tetrahedra of the 600-cell are replaced by their rectifications, Octahedra. Under each of the 120 vertices of the 600-cell new Icosahedra (the vertex polyhedron of the 600-cell) appeared; all their projections were already visible in the model of the 600-cell in Fig. 5.10. Each edge is shared by one Icosahedron and two Octahedra. Its Icosahedral projection, centered on an Icosahedral cell, is shown in Fig. A.4.


Fig. A.4: The Icosahedral projection of the Rectified 600-cell. This projection is the rectification of the Icosahedral projection of the 600-cell.

How to build: After studying the perspective-flattened Icosahedra in the model of the 600-cell, have a look at the Eusebeia page on the Rectified 600 cell. Also recommended is David Richter's page on the Rectified 600-cell.


Also, as for the other semi-regular polychora, all faces are Triangular. In all rectifications of regular polychora with Tetrahedral cells the vertex polyhedron is a prism, in this case it is Pentagonal. Since all faces are Triangular, these prisms are necessarily edge sections located under each vertex.

If you pay close attention to the model, you will be able to see several Archimedean solids in blue, starting with Icosidodecahedra - the rectifications of the Icosahedral sections of the 600-cell. These polyhedra are edge sections of the Rectified 600-cell. Because they have Icosahedral symmetry, they appear ``under'' the Icosahedral cells in 4-D space, around the central cells in this projection. Studying the model further, you will be able to see many flattened versions of those.

All these sections are the cells of 14 non-convex polychora, all of them edge facetings of the Rectified 600-cell and therefore represented by the same model. One of them is the Rectified icosahedral 120-cell, which has Great dodecahedra and Icosidodecahedra as cells (for more about the Icosahedral 120-cell, see the page on regular star polychora). These 14 edge-facetings are a sub-group of the 60 facetings of the Rectified 600-cell that are uniform, non-convex polychora.


Fig. A.5: The icosidodecahedral cell-first projection of the Rectified 120-cell.

How to build: Study the perspective-flattened Dodecahedra in the model of the 120-cell. Make models of Icosidodecahedra with similar flattening. Then have a look at the Eusebeia page on the Rectified 120 cell.
Picture taken by Jason Wu.


Finally, in Fig. A.5 we show the Icosahedral projection of the Rectified 120-cell. The Dodecahedra of the 120-cell are here replaced by their rectifications, Icosidodecahedra. Under each of the 600 vertices of the 120-cell, a Tetrahedron (the vertex figure of the 120-cell) appeared. Each edge is shared by a Tetrahedron and two Icosidodecahedra. This Icosahedral projection is necessarily centred on an Icosidodecahedral cell.

Truncations:

We now show a few examples of truncations. The first example is the Truncated 16-cell. In this polychoron, we cut the 8 vertices of the 16-cell, which produces 8 new polyhedral cells that are identical to the vertex figure of the 16-cell, Octahedra. However, the 16 Tetrahedral cells of the 16-cell were not rectified to Octahedra (as in the Rectified 16-cell, also known as the 24-cell), but instead truncated, becoming Truncated tetrahedra. All vertices are still identical, so that this new polychoron is still uniform. However, like the Truncated tetrahedron, this polychoron is no longer isotoxal: we have now not only different types of cells and faces, but also different types of edges. The same applies to the following polychora.


Fig. A.6a: The truncated 16-cell. This projection, centred on an Octahedron, is the truncation of the vertex-first projection of the 16-cell in Fig. 5.4.

How to Build: See the Eusebeia page on the Truncated 16-cell.


Fig. A.6b: The truncated 16-cell*. This projection, centred on two Truncated tetrahedra, is the truncation of the cell-first projection of the 16-cell in Fig. 5.4. For the same reason, it can represent two truncated 16-cells, depending on which Truncated tetrahedron is closest to us.


Fig. A.6c: A different perspective of the last model.


We cannot represent the Truncated tesseract, because it has Truncated cubes as cells. These have Octagonal faces, which as mentioned above cannot be represented properly in the Zometool system. However, we can represent the Bi- truncated tesseract, which is also the Bi-truncated 16-cell. This is a special type of truncation, where the Tetrahedral and Cubic cells of the two dual polychora are both bitruncated, resulting respectively in Truncated tetrahedra and Truncated octahedra.


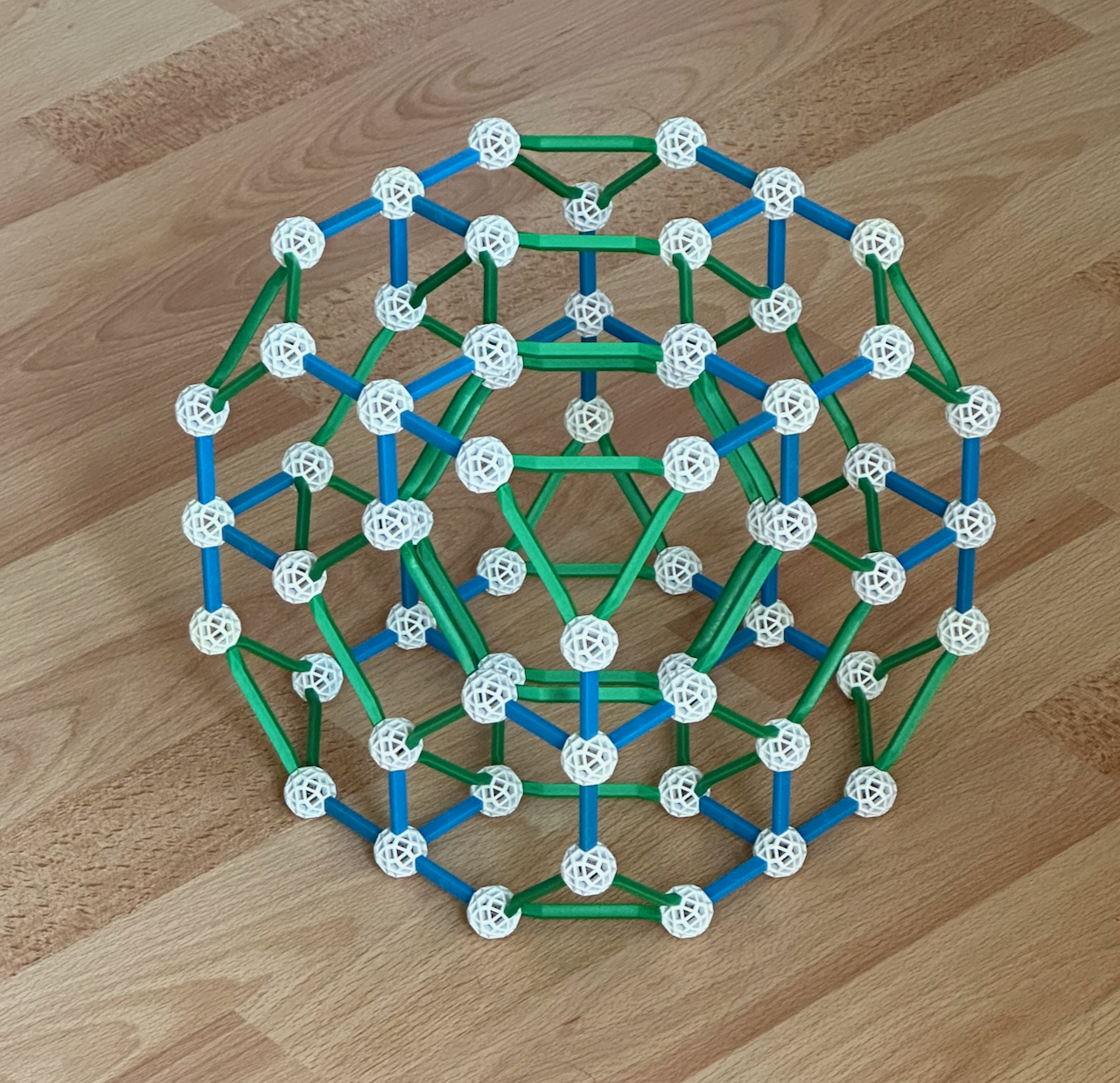
Fig. A.7a: The bitruncated Tesseract/16-cell. The projection is centred on a Truncated octahedron.

How to Build: See the Eusebeia page on the Bitruncated tesseract.


Fig. A.7b: The bitruncated 16-cell*. This projection is centred on two Truncated tetrahedra. It can represent two truncated 16-cells, depending on which Truncated tetrahedron is closest to us.


Fig. A.7c: A different perspective of the last model.


Another important example is the Truncated 24-cell. As in the Rectified 24-cell, we cut the 24 vertices of the 24-cell, which produces 24 new Cubic cells. However, the 24 Octahedral cells of the 24-cell are not rectified, but truncated into Truncated octahedra.


Fig. A.8: The truncated 24-cell. The projection, centred on a Truncated octahedron, is the truncation of the cell-first projection of the 24-cell.

How to Build: See the Eusebeia page on the Truncated 24-cell. For this particular projection, see the part on the "cantitrucated 16-cell".


Finally, we show the Truncated 600-cell, a model of its Icosahedral projection is shown below. It is similar to the Rectified 600-cell above, and it also has 120 Icosahedral cells. However, instead of 600 Octahedral cells, it has 600 Truncated tetrahedral cells.


Fig. A.9a: The Truncated 600-cell, here seen along one of its 5-fold symmetry axes.


Fig. A.9b: The same model as above, seen here from a 3-fold symmetry axis.

How to Build: See the Eusebeia page on the Truncated 600-cell


As for the Archimedean polyhedra, the vertices of truncated (or bi-truncated) polychora are reflections of points located on edges, this time on one of the six edges of the Goursat tetrahedron.

Other constructions:

A few other types of Wythoffian construnctions can also generate uniform polychora while reflecting points located in the four faces of the Goursat tetrahedron. An example of this with the symmetry of the 600-cell is the cantitruncated 600-cell (this page also shows how to make all Wythoffian constructions of polychora using vZome).

The most complex type of Wythoffian construction is the ommnitruncation, which reflects a vertex inside the Goursat tetrahedron. This means that in a polychoron generated this way, the number of vertices will be, for a particular symmetry, the same as the number of Goursat tetrahedra that tile the 3-sphere, which is the order of the associated symmetry group. There are two Zomable examples. The first is the Omnitruncated 5-cell (see vZome model), which is the 4-dimensional permutohedron and is therefore one of the rare uniform polychora that can fill space. Furthermore, this polychoron is twice as symmetric as the 5-cell, having the full extended pentachoric symmetry. This property is shared by the other omnitruncation of a self-dual polychoron, the 24-cell, which has twice the symmetry of the 24-cell.


Fig. A.10: The Omnitruncated 5-cell(*). The projection is centred on a Truncated octahedron.

How to Build: See the Eusebeia page on the Omnitruncated 5-cell.


The second is the Omnitruncated 120-cell. This polychoron has 14400 vertices, the number of symmetries of any object with full Hexacosichoric symmetry. Its Icosahedral projection is Zomable, but it dwarfs the complexity of the model in Figs. A.9a and b (see video).

This means that, for each symmetry, there are in principle 4 uniform polychora that result from reflecting the 4 vertices of the Goursat tetrahedron (2 regular and their 2 rectifications), six from the 6 edges of the Goursat tetrahedron (which include the truncations and bitruncations mentioned above), four from the 4 faces of the Goursat tetrahedron, and the Omnitruncated form that results from reflecting a point inside the Goursat tetrahedron. We thus come to a total of 15 uniform polychora for each type of polychoral symmetry. However, for the symmetries of self-dual forms, where a polychoron and its dual are identical (the same applying to their rectifications and other forms), we have a total of 9 uniform polychora.

Thus, the number of Archimedean polychora should be: However, as mentioned above, there are only 47. The reason is that three objects are being counted twice: the 24-cell is the rectification of the 16-cell, the Rectified 24-cell is also the "cantellated 16-cell" (see caption of Fig. 5.6) and the Truncated 24-cell is also the "cantitruncated 16-cell" (see caption of Fig. A.8). This situation is analogous to the cells of the 24-cell, Octahedra, which can be derived from the Tetrahedral and Octahedral symmetries. The number of Archimedean polychora derived from the symmetries of the 16-cell and 24-cell is thus 15 + 9 + 1 − 3 = 22.

The Grand antiprism:

The Grand antiprism was the last Archimedean polychoron to be discovered (in 1964 by John H. Conway and Michael Guy), who also proved that this is really the last one. This is an anomalous uniform polychoron in the sense that, unlike all other polychora discussed above, it has no Wythoffian construction.

The Grand antiprism and the aforementioned Snub 24-cell are diminished 600-cells; this means that their vertices and edges are subsets of the vertices and edges of the 600-cell. Since the 600-cell is Zomable, this implies that the Grand antiprism and the Snub 24-cell must be Zomable as well! A Zomable projection of the Snub 24-cell appears in Fig. 5.8. Below I show two Zomable projections of the Grand antiprism, both are derived by removing selected struts and vertices from the Icosahedral projection of the 600-cell.


Fig. A.11a: A projection of the Grand antiprism.
Picture by Aris Noutsos. Linked picture by Jason Wu.

How to Build: You can see a vZome model of this projection (together with other 3-D projections) at the start of this page.
When you study the model of the 600-cell in detail, you realize that there are six red axes going through the model (which are Decagons flattened into lines by the projection) and that, perpendicular to them, there are six blue Decagons defining an outer blue Icosidodecahedron. All we have to do is to remove one of the red axes and its perpendicular outer blue Decagon, together with their vertices and all the struts that connect to their vertices. You will then see an alignment of 10 Pentagonal antiprisms going through the center - in this Figure, we're looking through these. Along this direction, the Pentagonal antiprisms get progressively flattened as they approach the outer regions. In the perpendicular ring, another 10 Pentagonal antiprisms are seen ``sideways'', and completely flattened.


Fig. A.11b: Here is the second Zomable projection of the Grand antiprism!

How to Build: You can see a vZome model of this projection at the end of this page.
The derivation is the same as for Fig. A.11a, but using instead the other two types of Decagons that appear in the projection of the 600-cell: one type has its edges coinciding with the edges of the inner blue Icosahedron (connecting to the vertices of the outer blue Icosidodecahedron via short red struts) and a perpendicular one, with edges coinciding with the blue Dodecahedron, which connect with the vertices of the outer blue Icosidodecahedron via yellow struts. Apart from these and those missing in the model in Fig. A.11a, there are no additional types of Decagons in the Icosahedral projection of the 600-cell.

See also Eusebeia page on the Grand antiprism.


Its structure also helps understanding the structure of the 600-cell, in particular the fact that the latter can be decomposed in two disjoint perpendicular rings of 150 Tetrahedra each (which are "fused" to make the rings of 10 Pentagonal Antiprisms of the Grand antiprism), separated by a Clifford torus of 100 Tetrahedra with the two sets of 100 Tetrahedra that border that torus on each side.

Zomable Archimedean polychora and Triality

 We now investigate which Archimedean polychora are Zomable: Even more interesting is the fact that, apart from the Tesseract, the latter set of Zomable polychora is the full set of polychora generated by the demi-tesseractic symmetry, which is the 4-dimensional demi-hypercubic symmetry. Therefore, of all Archimedean polychora generated from the symmetry of the 16-cell and 24-cell, only the full set of ``Demi-tesseractic'' polychora are Zomable, plus the Tesseract! This situation is similar to that of the Archimedean solids with Tetrahedral and Octahedral symmetry, where only the full set of polyhedra derived from the demi-cubic symmetry (the Tetrahedral symmetry, which is the 3-dimensional demi-hypercubic symmetry, in green in Fig. A.2), plus the Cube (in blue in Fig. A.2) are Zomable.

Why the exceptions for the Tesseract and the Cube? As we've seen for the facetings of the 24-cell, the edges of the Tesseract are a subset of the edges of the 24-cell, so if the latter is Zomable, so is the former. The same applies therefore to its cells, all Cubic. It is logically necessary that the Cube is Zomable, because it is a cell not only of the Tesseract but also of two demi-tesseractic polychora, the Rectified 24-cell and the Truncated 24-cell.

Interestingly, the demi-tesseractic symmetry is the one that exhibits the phenomenon of triality. This means that the Demi-tesseractic polychora are not only Zomable, but they have many Zomable projections! We now investigate these.

Those derived from the symmetry of the 16-cell have three sets of Zomable ``trial'' projections, like the 16-cell itself, these include the green-blue projections shown above (which can be derived from the projections of the 16-cell in Fig. 5.4), three orthogonal pyritohedric projections (like the projections of the 16-cell in Fig. 7.1a) and three trial prismatic projections (like the projections of the 16-cell in Fig. 7.1b). These projections were calculated using vZome.

The blue-green projections of the Rectified tesseract are shown in Figs. A.3a and b. Below we show all remaining projections.


Fig. A.12a: The pyritohedric projection of the Rectified tesseract. This is centred on a Square face. The two other trial projections would have these central Squares in orthogonal planes, like the central edges of the 16-cell in Fig. 7.1a.


Fig. A.12b: One trial prismatic projection of the Rectified tesseract.


Fig. A.12c: Another trial prismatic projection of the Rectified tesseract.


Fig. A.12d: Another trial prismatic projection of the Rectified tesseract.

All three trial projections require 32 connectors, 24 B2 struts, 24 R2 struts, 24 Y2 struts and 24 R3 struts.


The blue-green projections of the Truncated 16-cell are shown in Figs. A.6a and b. Below we show all remaining projections.


Fig. A.13a: The pyritohedric projection of the Truncated 16-cell. Like the pyritohedric projection of the 16-cell, this is centred on an edge. The two other trial projections would have these central edges in orthogonal axes, like the central edges of the 16-cell in Fig. 7.1a. Note the similarity with Fig. A.6c.


Fig. A.13b: One trial prismatic projection of the Truncated 16-cell.


Fig. A.13c: Another trial prismatic projection of the Truncated 16-cell.


Fig. 13d: Another trial prismatic projection of the Truncated 16-cell.

The three trial projections require 48 connectors, 30 B2 struts, 30 R2 struts, 30 Y2 struts and 30 R3 struts.

These projections are truncations of the projections of the 16-cell that appear in Figs. 7.1a and b.
David Richter's detailed explanation of Triality shows the prismatic projections of the 16 cell and truncated 16-cell from a different perspective.


The blue-green projections of the Bitruncated 16-cell are shown in Figs. A.7a and b. Below we show all remaining projections.


Fig. A.14a: The pyritohedric projection of the Bitruncated 16-cell/Tesseract. Like the pyritohedric projection of the Rectified tesseract, this is centred on an Square face. The two other trial projections would have these central Squares in orthogonal planes, like the central edges of the 16-cell in Fig. 7.1a. Note the similarity with Fig. A.7c.


Fig. A.14b: One trial prismatic projection of the Bitruncated 16-cell/Tesseract.


Fig. A.14c: Another trial prismatic projection of the Bitruncated 16-cell/Tesseract.


Fig. A.14d: Another trial prismatic projection of the Bitruncated 16-cell/Tesseract.

The three trial projections require 96 connectors, 48 B2 struts, 48 R2 struts, 48 Y2 struts and 48 R3 struts.


The demi-tesseractic polychora derived from the 24-cell have only three Zomable projections each, like the 24-cell. Apart from the green-blue projections (Figs. 5.5a, 5.6 and A.8), these include a pyritohedric and a prismatic projection, which correspond to the projections of the 24-cell in Figs. 7.1a and b. However, in the prismatic projections of these polychora there are several intersections between red and yellow parts that are difficult to implement at a reasonable scale. For this reason, I only show here their pyritohedric projections, at least for now.

The blue-green projection of the Rectified 24-cell is shown in Fig. 5.6. Below we show one of the two remaining projections.


Fig. A.15: The pyritohedric projection of the Rectified 24-cell. This is the rectification of the pyritohedric projection of the 24-cell in Fig. 5.5b, and like it it has full Octahedral symmetry. It is centred on a Cube.


The blue-green projection of the Truncated 24-cell is shown in Fig. A.8. Below we show one of the two remaining projections.


Fig. A.16: The pyritohedric projection of the Truncated 24-cell. This is the truncation of the pyritohedric projection of the 24-cell in Fig. 5.5b, and like it it has full Octahedral symmetry. Like the previous projection, it is also centred on a Cube.


To conclude, we note the Wythoff construction can be applied to the flat analog of the regular polychora, the Cubic honeycomb. This results in many of the Archimedean honeycombs, the flat analogs of the Archimedean polychora, but not all, as several are Non-Wythoffian. These honeycombs are of practical interest for fields like architecture, engineering and crystallography.

As for polyhedra, relaxing the condition of convexity results in many more ``Archimedean'' star polychora, with more than 2000 known forms! These include the regular and partially regular star polychora as special cases.


Paulo's polytope site.