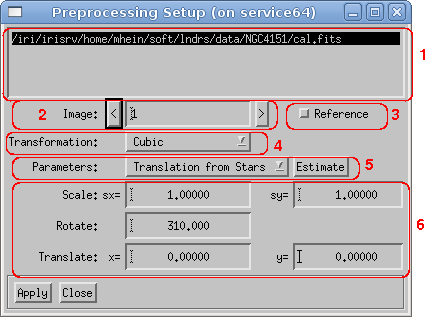
Because all reconstruction algorithms require identical mapping of the target images onto the sky, the preprocessing is an essential step. The standard preprocessing algorithm uses five parameters to rotate, scale and translate an image. Therefore, the parameters specified in the dialog window (see figure 1) must be precise.

Figure 1: Dialog window containing the preprocessing parameters.

The following parameters are presented in the preprocessing setup:

1. The list of files containing calibrated images is used to select the file for which the preprocessing parameters should be inspected and/or modified.
2. If a file contains more than one image (different position angles), the <- and >-buttons are used to select a specific image number.
3. It is possible to specify an image as a reference image. The orientation of that image is then used as a reference if the transformation parameters of the other images must be calculated.
4. Several algorithms are available for transforming an image:
   • Nearest: This is a fast transformation algorithm.
   • Bilinear: A simple bilinear interpolation schema is used for the transformation.
   • Cubic: A more sophisticated cubic interpolation schema is used.
   • Fourier: A fourier space method is used for rotation and translation.
5. There are several ways to determine the transformation parameters:
   • Use FITS Header: The instrument-specific keyword values in the FITS header of the calibrated data are used to calculate the transformation parameters. This method is not implemented!
   • Rotation from Stars: The reference stars are used to calculate the rotation angle.
   • Translation from Stars: The reference stars are used to calculate the translation vector.
6. All available transformation parameters use up to five parameters for scaling, rotation, and translation. Image scaling is currently not implemented.

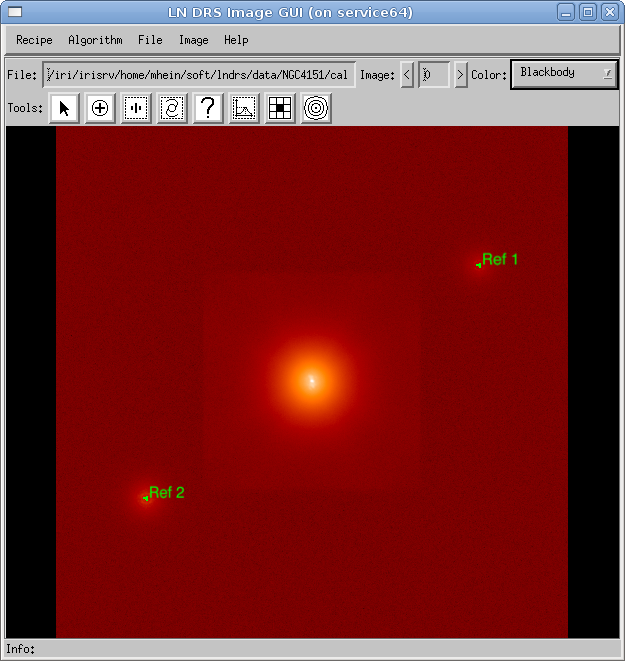
If the FITS header keywords are available and sufficient, they are preferred over a calculation of the transformation parameters. If an explicit calculation of the parameters is required, a set of reference points (reference stars) is needed. These reference stars are created by using the reference star tool. During an inspection of the calibrated data, several reference points or stars are identified. At least two stars are needed in order to calculate the rotation angle. All reference stars must be defined in each calibrated image, and each star must have the same reference number in each image. Figure 2 shows a calibrated image with two defined reference stars. Because the calculation of the rotation angle or translation vector works only between two images, one image must be marked as the reference image (see Reference checkbox in the preprocessing parameter dialog window).

Figure 2: Calibrated data.

The reference star tool (see section Tools) provides the usual image navigation interface (zooming and panning of an image) and allows the creation, modification, and deletion of reference stars.

Figure 3: Graphical representation and dialog window of a reference star.

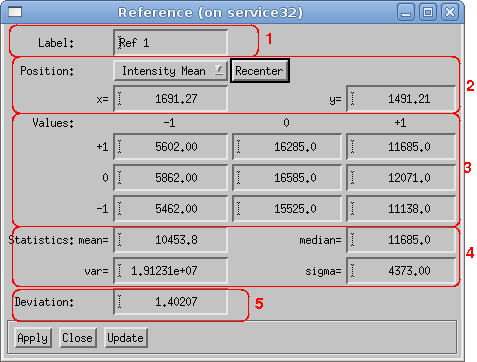The dialog window of a reference star shows the following information:

1. The label of a reference star is automatically created and updated.
2. The position of a reference star uses fractional values. It is possible to recenter the reference star or set the position explicitly. The Update button recalculates the statistical information after changing the position of a reference star.
3. The values of the pixel in the center of the reference star and the eight neighbors are shown. The orientation in the dialog window and in the displayed image is identical.
4. The statistical information uses only the neighbor pixels; the central pixel is ignored.
5. The deviation describes the pixel value as mean + σ × deviation. If the deviation is too big, it is possible that the central pixel is a defect pixel.

The code snippet in source 1 contains the method of calculating the rotation angle of an image according to the fixed rotation angle of a reference image. For each reference star, the basic algorithm calculates the angle between the x-axis and the line from the center of the reference star set (center of gravity) to that reference star. The distance of that star from the center of gravity determines the significance (weight) of the calculated angle.

The code snippet in source 2 contains the method of calculating the translation vector of an image according to the fixed position of a reference image. This method requires a precise rotation angle because this angle is used to rotate the reference stars in an image and calculate the vectors between the same stars in the reference image.

If a closer look at a reference star (high magnification) shows that the position is not correct, some methods to automatically recenter the graphical object exist:

• Intensity Peak: Searches the highest pixel value in a part of the image (20 pixels), which is then used as the new position. The new position has integral coordinates. This method is sensitive to noise and can give incorrect coordinates for weak reference stars.
• Intensity Mean: Uses the weighted center of all pixels in a small window that have values above a certain limit. The new position has fractional coordinates. This method is not sensitive to a tilted background (for example, the object halo).
• Fourier Phase: Uses the fourier phase of the smallest frequency in a small image part as a displacement vector. This method is sensitive to a tilted background.