Pulsar mass measurements and tests of general relativity
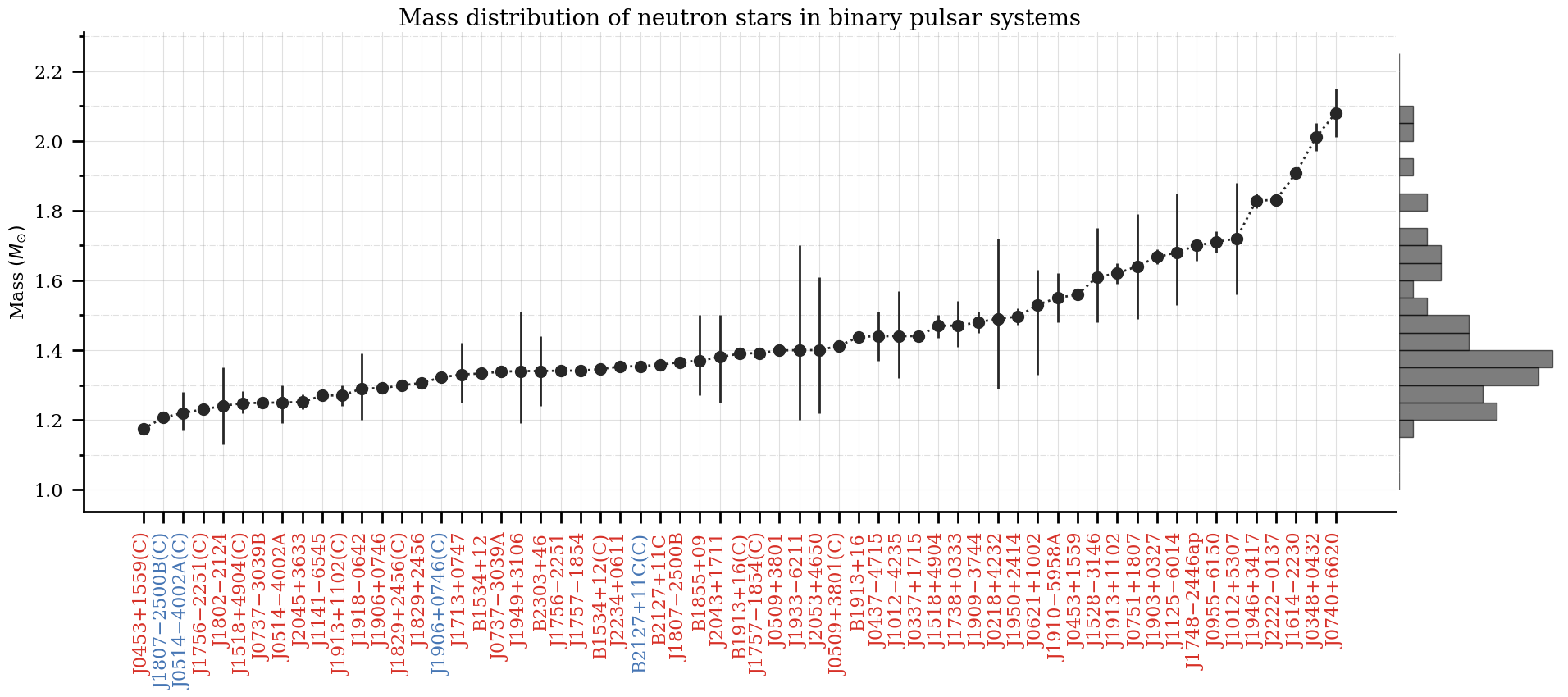
Fig. 1: Neutron star mass measurements presented in the table below, sorted by increasing
mass. The letter C in parentheses indicates a companion to a pulsar that is itself not a pulsar. The
names in blue are the cases where such a companion could be a NS or a massive WD, the names in red
are for confirmed NSs, as the mass values in the main table. The error bars in orange denote
multiple recent measurements of the same NS mass. On the right, we have a histogram of
the NS masses. Figure created by Vivek V. Krishnan. For a version without the histogram, click here
The 3-part table below only includes systems for which there is either no mass transfer nor significant mass loss, i.e., ``clean'' systems, where tests of general relativity are in principle possible. This page is therefore not meant to be comprehensive, but merely my personal reference on precise NS masses and tests of gravitational theories.
See the latest changes to this page below.
The mass measurements or constraints are highlighted in red for NSs, in blue for objects that can either be NSs or massive WDs, and gray for WDs (and 1 MS star). Each row has one stellar system.
I indicate in boldface the constraints that yield, according to GR, the most precise mass values or limits, or that were used to derive them in the literature. These mass constraints are derived from radio timing and, in some cases, the combination of timing with optical measurements of their white dwarf companions. The 1-σ uncertainties on the masses are indicated by the numbers in parentheses, they apply to the last digits of the values. The types of constraints are explained immediately after the main tables. In cases where there are more than two mass constraints, one might be in the presence of a test of general relativity. For the reference on each mass constraint, click on its symbol.
-
The top table lists all 61 precise (where the 1-σ
uncertainty is smaller than 15% of the measurement) NS mass measurements, plus 3 precise
mass measurements for objects that can either be NSs or massive WDs, in a total of
51 stellar systems.
I list the mass of the binary only if it constrains the individual masses of the components. This happens for several eccentric systems, where the binary mass can be derived directly from the rate of advance of periastron. - The middle table lists 28 systems where the only available post-Keplerian effect is the rate of advance of periastron. In these systems we can only estimate the mass of the binary system, not the individual component masses. The systems listed are those where the binary mass estimates have relative precisions better than 15%. Using the mass functions of these systems and the binary mass, we can estimate maximum limits for the pulsar mass and minimum limits for the companion masses.
- The last table lists all confirmed (25) and candidate (11) pulsar - neutron star systems that have been published. The members of this list repeat several systems presented in the previous two parts. It also includes systems for which no mass constraints have been published, apart from the mass functions.
Acronyms used below:
| NS | - neutron star. |
| PSR | - pulsar, a NS for which we can detect periodic pulsations |
| yPSR | - young pulsar (i.e., no sign of recycling) |
| MSP | - millisecond pulsar (recycled pulsar with F0 > 60 Hz), |
| WD | - white dwarf; He WD - Helium WD |
| MS | - main sequence star, |
| BH | - black hole, |
| GC | - globular cluster, |
| GR | - general relativity. |
| 1. Systems with individual NS mass measurements | ||||||||||
| PULSAR |
F0 (Hz) |
Pb (days) |
x (s) |
e | MT (M☉) |
Mp (M☉) |
Mc (M☉) |
Mass constraints | Geodetic precession | Notes |
|---|---|---|---|---|---|---|---|---|---|---|
| J0218+4232 | 430.461 | 002.02885 | 001.98443 | 0.0000063(2) | 1.49(+23/−20) | 0.179(+18/−16) | r, s | a | MSP - He WD system. | |
| J0337+1715 | 365.953 | 001.62940 327.25512 |
001.21753 074.67234 |
0.000699036(+37/−42) 0.0352911721(+20/−28) |
1.4380(+12/−11) | 0.19755(+15/−14) 0.41012(+31/−29) |
i, q | a | First pulsar in a triple star system. Two companions are He WDs, hence the two companion masses. The two sets of Keplerian parameters are for the orbit of the inner system (containing MSP and WD) and the orbit of the outer WD with the inner system. q is measured independently for inner system. This system yields the best test of the Universality of free fall to date (see also the first and second versions of this test). | |
| J0348+0432 | 025.561 | 000.10242 | 000.14098 | 0.0000020(10) |
2.01(4) 1.806(36) |
0.172(3) 0.154(3) |
q, mWD, GWa q, GWa |
a | PSR - He WD system. First massive NS in a relativistic orbit. Latest orbital decay measurements disagrees with prediction derived from spectroscopic mass measurements. If the observed orbital variation is only the orbital decay due to GW emission predicted by GR, the components masses are significantly smaller than their spectroscopic estimate. | |
| J0437−4715 | 173.688 | 005.74104 | 003.36670 | 0.000019180(3) | 1.418(44) | 0.221(4) | r, s | a | MSP - He WD system. Very high timing precision. Full 3-D position, velocity, orbital orientation and masses are known. | |
| J0453+1559 | 021.843 | 004.07247 | 014.46679 | 0.11251847(8) | 2.734(4) | 1.559(5) | 1.174(4) | p, h3 | u | PSR - NS. Asymmetric DNS. Companion star is lightest NS known. |
| J0509+3801 | 013.065 | 000.37958 | 002.05046 | 0.586409(3) | 2.81071(14) | 1.399(6) | 1.412(6) | p, γ, GW | u | PSR - NS. Highly eccentric, similar to the Hulse-Taylor pulsar. |
| J0514−4002A | 200.378 | 018.78518 | 036.2909 | 0.8879765(3) | 2.47346(28) | 1.39(3) | 1.08(3) | p, γ | u | MSP - massive WD companion. System formed through exchange encounter in GC NGC 1851. Ongoing encounter with a third object; this might add a small (order 10−3) contribution to the observed periastron advance, so it is possible total mass might be a factor of ~10−3 different. |
| J0621+1002 | 034.657 | 008.31868 | 012.03207 | 0.00245744(4) | 2.32(8) | 1.53(+10/−20) | 0.76(+28/−7) | p, s | a | PSR - Massive WD system. |
| J0737−3039A
J0737−3039B |
044.054
000.360 |
000.10225 | 001.41503
001.516 |
0.08777702(6) | 2.587052(+9/−7) | 1.338185(+12/−14) 1.248868(+13/−11) |
1.338185(+12/−14) 1.248868(+13/−11) |
R, p, γA, s, rA, GW, GB | no
yes, yes |
PSR - yPSR. The only double pulsar known. Most highly inclined binary pulsar known. Seven mass constraints, which determine the masses and yield 5 independent GR tests. Most precise measurements of NS masses and most precise measurement of the orbital decay ever. Detection of second-order effects in the rate of advance of periastron (with contribution from Lense-Thirring effect) and Shapiro delay. |
| J0740+6620 | 346.532 | 004.76694 | 003.97756 | 0.00000507(4) | 2.08(7) | 0.253(+6/−5) | r, s | a | MSP- Massive WD system, likely most massive NS. | |
| J0751+1807 | 287.458 | 000.26314 | 000.39661 | 0.0000005(11) | 1.64(15) | 0.16(1) | s, GWa | a | MSP - He WD system, only case where mass is derived from s and assumption that GWa is as given by GR. | |
| J0955−6150 | 500.160 | 024.57840 | 013.28248 | 0.11750575(1) | 1.96(2) | 1.71(3) | 0.254(2) | p, h3, ς | u | Eccentric MSP - He WD system. |
| J1012−4235 | 322.462 | 037.97246 | 021.26307 | 0.00034572(1) | 1.44(+13/−12) | 0.270(+16/−15) | h3, ς | a | MSP - He WD system. | |
| J1012+5307 | 190.267 | 000.60467 | 000.58182 | 0.0000012(3) | 1.72(16) | 0.165(15) | q, mWD, GWa | a | MSP - He WD system. Useful constraints on dipolar GW emission (a, b). | |
| J1125−6014 | 380.173 | 008.75260 | 008.33919 | 0.000000615(11) | 1.68+(+17/−15) | 0.33(2) | r, s | a | MSP - Light CO WD system. | |
| J1141−6545 | 002.539 | 000.19765 | 001.85892 | 0.171876(1) | 2.28967(6) | 1.27(1) | 1.02(1) | p, γ, GWa | yes | yPSR, formed after the companion, which is a massive WD. The fast rotation of the WD induces a detectable precession in the orbit, a significant part of which is relativistic (the Lense-Thirring effect). |
| J1227−6208 | 028.962 | 006.72102 | 023.20067 | 0.00114918(4) | 1.54(15) | 1.40(7) | p, h3, ς | u | PSR - massive WD system. WD companion could me most massive in this list. | |
| J1518+4904 | 024.428 | 008.63400 | 020.03949 | 0.249484383(9) | 2.7186(7) | 1.470(+30/−34) | 1.248(+35/−29) | p, s | u | PSR - NS. |
| J1528−3146 | 016.441 | 003.18035 | 011.45230 | 0.0002137(2) | 2.94(+21/−20) | 1.61(+14/−13) | 1.33(+8/−7) | r, s, p | a | PSR - massive WD system. WD companion could me most massive in this list. |
| B1534+12 | 026.382 | 000.42074 | 003.72946 | 0.27367740(4) | 2.678463(4) | 1.3330(2) | 1.3455(2) | p, γ, r, s, GW, G | yes | PSR - NS. Orbital decay (GW) has been measured precisely but does not provide a test of GR because of lack of precise knowledge of distance. |
| J1543−5149 | 486.154 | 008.06077 | 006.48029 | 0.00002133(3) | 1.349(+43/−61) | 0.2233(+45/−61) | h3, ς | a | MSP - He WD system. | |
| J1614−2230 | 317.379 | 008.68662 | 011.29120 | 0.000001333(8) | 1.908(16) 1.94(3) |
0.493(3) 0.495(5) |
r, s r, s | a | MSP- Massive WD system, massive MSP. | |
| J1713+0747 | 218.811 | 067.82513 | 032.34242 | 0.0000749402(6) | 1.33(+9/−8) 1.35(7) |
0.289(+13/−11) 0.292(11) |
h3, ς r, s |
a | MSP - He WD system. This system surrently provides the best pulsar limit on the variation of the gravitational constant, on violations of the universality of free fall and on the α3 parameter. | |
| J1738+0333 | 170.937 | 000.35479 | 000.34343 | 0.00000034(11) | 1.47(+7/−6) | 0.181(+7/−5) | q, mWD, GWa | a | MSP - He WD system. This system yields useful constraints on dipolar GW emission (a, b) and the best limits on igravitational Local Lorenz Invariance violation parameter α1 | |
| J1748−2446ap | 267.044 | 021.38817 | 013.20131 | 0.905186(4) | 1.997(6) | 1.700(+15/−45) | 0.294(+46/−14) | p, γ | u | MSP - He WD. Located in Terzan 5, system is highly eccentric and likely perturbed by close stellar encounters. |
| J1756−2251 | 035.135 | 000.31963 | 002.75646 | 0.1805694(2) | 2.56999(6) | 1.341(7) | 1.230(7) | p, γ, s, GW | no | PSR - NS. Low-mass NS companion. No geodetic precession for pulsar, indicating alignment of its spin axis with orbital angular momentum. |
| J1757−1854 | 046.518 | 000.18354 | 002.23781 | 0.6058174(3) | 2.732876(8) | 1.3412(4) | 1.3917(4) | p, γ, h3, ς GW | yes | PSR - NS. Most accelerated binary, largest relative velocity, five measured PK parameters. Second-formed NS significantly more massive than first-formed NS. |
| J1802−2124 | 079.066 | 000.69889 | 003.71885 | 0.00000248(5) | 1.24(11) | 0.78(4) | r, s | a | MSP - massive WD system. | |
| J1807−2500B | 238.881 | 009.95667 | 028.92039 | 0.747033198(40) | 2.57190(73) | 1.3655(21) | 1.2064(20) | p, ς, h3 | u | MSP - massive compact companion. System formed through exchange encounter in GC NGC 6544. Companion is either a massive WD or NS, so this could be a MSP - NS system. |
| J1829+2456 | 024.384 | 001.17603 | 007.23684 | 0.1391435(3) | 2.60551(38) | 1.306(7) | 1.299(7) | p, s | u | PSR - NS. |
| B1855+09 | 186.494 | 012.32717 | 009.23078 | 0.00002170(3) | 1.37(+13/−10) 1.59(+21/−18) |
0.244(+14/−12) 0.268(+22/−19) |
r, s, h3, ς |
a | MSP - He WD system. First measurement of Shapiro delay in a binary pulsar. | |
| J1903+0327 | 465.135 | 095.17412 | 105.59346 | 0.436678409(3) | 2.697(29)* | 1.667(21)* | 1.029(8)* | p, h3, ς, q | u | First MSP outside GCs with eccentric orbit. MS companion. System likely originated as a triple. *Masses indicated to 99.7% C.L. as uncertainties are not Gaussian. |
| J1906+0746 | 006.941 | 000.16599 | 001.41995 | 0.0852996(6) | 2.6134(3) | 1.291(11) | 1.322(11) | p, γ, GW, G | yes | yPSR - massive compact companion. The pulsar (only 110 kyr old) is the second-formed compact object in the system. Companion could be a recycled NS as in most other PSR - NS systems, but it could also be a massive WD, as in the cases of J1141−6545 and B2303+46. |
| J1909−3744 | 339.316 | 001.53345 | 001.89799 | 0.000000115(7) | 1.48(3) 1.492(14) 1.45(3) |
0.208(2) 0.209(1) 0.205(3) |
r, s
r, s r, s |
a | MSP - He WD system. First MSP with a precise mass. Very high timing precision and high inclination. Useful constraints on dipolar GW emission (a, b). | |
| J1910−5958A | 306.167 | 000.83711 | 001.20605 | 0.00000082(3) | 1.55(7) | 0.202(6) | r, s, q, mWD | a | MSP - He WD system in GC NGC 6572. | |
| J1913+1102 | 036.650 | 000.20625 | 001.75462 | 0.089531(2) | 2.8887(6) | 1.62(3) | 1.27(3) | p, γ, GW | u | PSR - NS. Most massive among these systems, pulsar is most massive NS in a PSR - NS system. First known member of new population of merging, asymmetric DNSs. |
| B1913+16 | 016.940 | 000.32299 | 002.34178 | 0.6171340(4) | 2.828378(7) | 1.438(1) | 1.390(1) | p, γ, GW, h3, ς | yes | PSR - NS. The Hulse-Taylor binary. First binary pulsar discovered. First NS mass measurements. Orbital decay was the first GR test in a binary pulsar, and first radiative test anywhere. This showed that gravitational waves exist. |
| J1918−0642 | 130.790 | 010.91318 | 008.35047 | 0.000020340(18) | 1.29(+10/−9) | 0.231(10) | r, s | a | MSP - He WD system. | |
| J1933−6211 | 282.212 | 012.81941 | 012.28157 | 0.00000126(2) | 1.4(+3/−2) | 0.43(5) | r, s | a | MSP - CO WD system. | |
| J1943+2210 | 077.699 | 000.37205 | 002.57980 | 0.0000016(4) | 1.84(+11/−9) | 1.03(+4/−3) | r, s | u | PSR - Massive WD system. Massive pulsar, compact orbit. | |
| J1946+3417 | 315.445 | 027.01995 | 013.86907 | 0.134495389(17) | 2.094(22) | 1.828(22) | 0.2556(19) | p, h3, ς | u | Eccentric MSP - He WD system. Massive MSP. |
| J1949+3106 | 076.114 | 001.94954 | 007.28865 | 0.000043122(35) | 1.34(+17/−15) | 0.81(+6/−5) | h3, ς, p | a | MSP - massive WD system. | |
| J1950+2414 | 232.300 | 022.19137 | 014.21994 | 0.07981173(4) | 1.779(25) | 1.496(23) | 0.2975(+46/−38) | p, h3 | u | Eccentric MSP - He WD system. |
| J2023+2853 | 088.270 | 000.71823 | 004.00222 | 0.0000131(6) | 1.28(+6/−6) | 0.85(2) | r, s | u | PSR - Massive WD system. | |
| J2043+1711 | 420.189 | 001.48229 | 001.62396 | 0.00000489(13) | 1.38(+12/−13) | 0.173(10) | r,s | a | MSP - He WD system. | |
| J2045+3633 | 031.564 | 032.29784 | 046.94080 | 0.017212447(6) | 2.127(31) | 1.251(21) | 0.873(+16/−14) | p, h3, ς | a | MSP - massive WD system. |
| J2053+4650 | 079.652 | 002.45250 | 008.80430 | 0.0000089(1) | 1.40(+21/−18) | 0.86(+7/−6) | h3, ς | a | MSP - massive WD system. | |
| B2127+11C | 032.755 | 000.33528 | 002.51845 | 0.681395(2) | 2.71279(13) | 1.358(10) | 1.354(10) | p, γ, GW | yes | PSR - massive compact companion. Formed through exchange encounter in GC NGC 7078 (M15), companion could be a massive WD, but generally assumed to be a NS given the large mass. Acceleration of system in the cluster precludes further improvements in precision of radiative test of GR. |
| J2222−0137 | 030.471 | 002.44576 | 010.84802 | 0.00038092(1) | 3.150(14) | 1.831(10) | 1.3194(40) | r, s, p, GWa | a | PSR - massive WD system. Useful constraints on dipolar GW emission (a, b). |
| J2234+0611 | 279.597 | 032.00140 | 013.93737 | 0.129274035(8) | 1.6518(+33/−35) | 1.353(+14/−17) | 0.298(+15/−12) | h3, p | u | Eccentric MSP - He WD system. Full 3-D position, velocity, orbital orientation and masses are known. |
| B2303+46 | 000.937 | 012.33954 | 032.6787 | 0.658369(9) | 2.64(5) | 1.34(10) | 1.30(10) | p, mWD | u | yPSR. Formed after the companion, which is a massive WD. |
| 2. Systems with binary mass measurements only | ||||||||||
| PULSAR | F0 (Hz) |
Pb (days) |
x (s) |
e | MT (M☉) |
Mp (M☉) |
Mc (M☉) |
Mass constraints | Geodetic precession | Notes |
| J0024−7204H | 311.493 | 002.35770 | 002.15281 | 0.0705585(7) | 1.665(7) | < 1.49 | > 0.175 | f, p | u | MSP with likely He WD companion. Located in GC NGC 104 (47 Tuc). |
| J0514−4002E | 178.701 | 007.44790 | 027.8192 | 0.70793232(85) | 3.8870(45) | < 1.79 | > 2.09 | f, p | u | MSP - massive compact companion. Most massive system in this list. System formed through exchange encounter in GC NGC 1851. Companion is either a very massive NS or a light BH. Limits on the individual masses derived from non-detection of the Shapiro delay. |
| J0528+3529 | 012.782 | 011.72618 | 031.43468 | 0.2901088(10) | 2.90(12) | < 1.8 | > 1.2 | f, p | u | PSR - NS. |
| J1018−1523 | 012.026 | 008.98393 | 026.15662 | 0.227749(2) | 2.3(3) | < 1.2 | > 1.1 | f, p | u | PSR - NS. |
| J1208−5936 | 034.826 | 000.63157 | 004.2570(4) | 0.347988(1) | 2.586(5) | < 1.48 | > 1.10 | f, p | u | PSR - NS. |
| J1325−6253 | 034.520 | 001.81559 | 007.57391 | 0.0640091(7) | 2.57(6) | < 1.59 | > 0.98 | f, p | u | PSR - NS. |
| J1411+2551 | 016.012 | 002.61586 | 009.20514 | 0.1699308(4) | 2.538(22) | < 1.62 | > 0.92 | f, p | u | PSR - NS. |
| B1516+02B | 125.835 | 006.85845 | 003.04826 | 0.137839(2) | 2.157(28) | < 2.05 | > 0.14 | f, p | u | MSP - WD system, located in GC NGC 5904 (M5). |
| J1617−2258A | 231.572 | 000.78915 | 000.46421 | 0.53744(3) | 1.67(6) | < 1.60(6) | > 0.083 | f, p | u | MSP - WD system, located in GC NGC 6093 (M80). |
| J1618−3921 | 083.422 | 022.74560 | 010.27828 | 0.02741231(1) | 1.42(+20/−19) | < 1.39 | > 0.17 | f, p | u | Eccentric MSP - He WD system. Very likely a member of a triple system. |
| J1748−2446I | 104.491 | 001.328 | 001.818 | 0.428 | 2.17(2) | < 1.96 | > 0.24 | f, p | u | MSP - WD system, located in GC Terzan 5. |
| J1748−2446J | 012.447 | 001.102 | 002.454 | 0.350 | 2.20(4) | < 1.96 | > 0.38 | f, p | u | PSR - WD system, located in GC Terzan 5. |
| J1748−2446am | 340.853 | 000.80011 | 000.93782 | 0.204736(9) | 1.85(2) | < 1.7 | > 0.15 | f, p | u | MSP - WD system, located in GC Terzan 5. |
| J1748−2446ao | 439.681 | 057.55568 | 062.31393 | 0.32488898(8) | 3.166(24) | < 2.23 | > 0.93 | f, p | u | MSP with massive companion. System formed through exchange encounter in Terzan 5. Companion is either a massive WD or NS, so this could be a MSP - NS system. |
| J1748−2446au | 219.866 | 005.97946 | 006.54572 | 0.025695(1) | 1.82(7) | < 1.53 | > 0.30 | f, p | u | MSP - WD system, located in GC Terzan 5. |
| J1748−2021B | 059.665 | 020.55001 | 004.46699 | 0.5701606(15) | 2.92(15) | < 3.24 | > 0.11 | f, p | u | PSR - WD system, located in GC NGC 6440. Possibly massive pulsar. |
| J1750−37A | 008.961 | 017.33428 | 024.39312 | 0.712431(2) | 1.97(15) | < 1.65 | > 0.53 | f, p | u | PSR - WD system, located in GC NGC 6441. |
| J1759+5036 | 005.681 | 002.04298 | 006.82461 | 0.30827(12) | 2.679(12) | < 1.84 | > 0.83 | f, p | u | PSR - NS. |
| B1802−07 | 043.288 | 002.61676 | 003.92059 | 0.21206(2) | 1.62(7) | < 1.33 | > 0.29 | f, p | u | PSR - WD system, located in GC NGC 6539. |
| J1811−1736 | 009.599 | 018.77917 | 034.7827 | 0.828011(9) | 2.57(10) | < 1.74 | > 0.93 | f, p | u | PSR - NS. |
| J1823−3021G | 164.169 | 001.54014 | 003.00331 | 0.380466(6) | 2.65(7) | < 2.4 | > 0.44 | f,p | u | MSP - massive compact companion. System formed through exchange encounter in GC NGC 6624. Companion is either a massive WD or NS, so this could be a MSP - NS system. |
| J1824−2452C | 240.484 | 008.07781 | 007.35739 | 0.8470437(8) | 1.616(4) | < 1.367 | > 0.245 | f, p | u | MSP - WD, located in NGC 6626 (M28). System is highly eccentric and likely perturbed by close stellar encounters. |
| J1846−0513 | 042.791 | 000.61302 | 004.75647 | 0.2085888(9) | 2.6287(35) | < 1.35 | > 1.28 | f, p | u | PSR - NS. |
| J1901+0658 | 013.202 | 014.45477 | 032.40204 | 0.3662392(5) | 2.79(7) | < 1.68 | > 1.11 | f, p | u | PSR - NS. |
| J1930−1852 | 005.390 | 045.06000 | 086.89027 | 0.39886334(15) | 2.54(3) | < 1.25 | > 1.30 | f, p | u | PSR - NS. Largest orbital period for this type of system. |
| J1946+2052 | 058.962 | 000.07849 | 001.15432 | 0.063848(9) | 2.50(4) | < 1.31 | > 1.18 | f, p | yes | PSR - NS. Shortest orbital period for this type of system. |
| J1953+1847D | 009.933 | 010.9380 | 032.0634(1) | 0.628921(3) | 2.63(8) | < 1.4 | > 1.1 | f,p | u | PSR - NS system. Located in the GC NGC 6838 (M71). Despite the location in a GC, the system is very unlikely to have formed in an exchange encounter. Its characteristics indicate it is a Pulsar - NS system. |
| J2140−2311B | 076.983 | 006.21565 | 019.5222(7) | 0.87938(2) | 2.53(8) | < 1.43 | > 1.11 | f,p | u | MSP - massive compact companion. System formed through exchange encounter in GC NGC 7099 (M30). Companion is either a massive WD or NS, so this could be a MSP - NS system. |
| J2150+3427 | 001.528 | 010.59213 | 025.48802 | 0.601494(2) | 2.59(13) | < 1.67 | > 0.98 | f, p | u | Pulsar with massive companion in eccentric orbit. Pulsar is very slow, and was likely (mildly) recycled. If it is the second-formed object in the system, then the companion (the primary) could be a massive WD. |
| 3. Confirmed and possible pulsar - neutron star systems (Important: most systems were already listed above) |
||||||||||
| PULSAR | F0 (Hz) |
Pb (days) |
x (s) |
e | MT (M☉) |
Mp (M☉) |
Mc (M☉) |
Mass constraints | Geodetic precession | Notes |
| J0453+1559 | 021.843 | 004.07247 | 014.46679 | 0.11251847(8) | 2.734(4) | 1.559(5) | 1.174(4) | p, h3 | u | Confirmed. Asymmetric DNS. Companion star is lightest NS known. |
| J0509+3801 | 013.065 | 000.37958 | 02.05046(3) | 0.586409(3) | 2.81071(14) | 1.399(6) | 1.412(6) | p, γ, GW | u | Confirmed. Highly eccentric, similar to the Hulse-Taylor pulsar. |
| J0514−4002E | 178.701 | 007.44790 | 027.8192 | 0.70793232(85) | 3.8870(45) | < 1.79 | > 2.09 | f, p | u | Candidate. MSP - massive compact companion. System formed through exchange encounter in GC NGC 1851. Companion is either a very massive NS or a light BH. |
| J0528+3529 | 012.782 | 011.72618 | 031.43468 | 0.2901088(10) | 2.90(12) | < 1.8 | > 1.2 | f, p | u | Confirmed. |
| J0737−3039A
J0737−3039B |
044.054
000.360 |
000.10225 | 001.41503
001.516 |
0.08777702(6) | 2.587052(+9/−7) | 1.338185(+12/−14) 1.248868(+13/−11) |
1.338185(+12/−14) 1.248868(+13/−11) |
R, p, s, γA, rA, GW, GB | no
yes, yes |
Confirmed. The only double pulsar known. Companion is a young, non-recycled pulsar. |
| J1018−1523 | 012.026 | 008.98393 | 026.15662 | 0.227749(2) | 2.3(3) | < 1.2 | > 1.1 | f, p | u | Confirmed. |
| J1155−6529 | 012.68 | 003.67 | 015.34 | 0.26 | - | [1.4] | > 1.27 | f | u | Confirmed. |
| J1208−5936 | 034.826 | 000.63157 | 004.2570(4) | 0.347988(1) | 2.586(5) | < 1.48 | > 1.10 | f, p | u | Confirmed. |
| J1325−6253 | 034.520 | 001.81559 | 007.57391 | 0.0640091(7) | 2.57(6) | < 1.59 | > 0.98 | f, p | u | Confirmed. |
| J1411+2551 | 016.012 | 002.61586 | 009.20514 | 0.1699308(4) | 2.538(22) | < 1.62 | > 0.92 | f, p | u | Confirmed. |
| J1518+4904 | 024.428 | 008.63400 | 020.03949 | 0.249484383(9) | 2.7186(7) | 1.470(+30/−34) | 1.248(+35/−29) | p, s | u | Confirmed. |
| B1534+12 | 026.382 | 000.42074 | 003.72946 | 0.27367740(4) | 2.678463(4) | 1.3330(2) | 1.3455(2) | p, γ, r, s, GW, G | yes | Confirmed. Orbital decay (GW) has been measured precisely but does not provide a test of GR because of lack of precise knowledge of distance. |
| J1748−2446ao | 439.681 | 057.55568 | 062.31393 | 0.32488898(8) | 3.166(24) | < 2.23 | > 0.93 | f, p | u | Candidate. MSP with massive companion. System formed through exchange encounter in Terzan 5. Companion is either a massive WD or NS, so this could be a MSP - NS system. |
| J1748−2021B | 059.665 | 020.55001 | 004.46699 | 0.5701606(15) | 2.92(15) | < 3.24 | > 0.11 | f, p | u | Candidate. Total mass consistent with PSR - NS system. If companion is a NS, then the system formed through exchange encounter. This would imply a very low orbital inclination. Located in GC NGC 6440. |
| J1753−2240 | 010.511 | 013.63757 | 018.11537 | 0.303582 | - | [1.4] | > 0.49 | f | - | Confirmed. Pulsar is recycled. |
| J1755−2550 | 003.173 | 009.69633 | 012.28441 | 0.08935(2) | - | [1.3] | > 0.39 | f | - | Candidate. yPSR - massive compact companion. The pulsar (only 2.1 Myr old) is the second-formed compact object in the system. Companion could be a recycled NS as in most other PSR - NS systems, but it could also be a massive WD, as in the cases of J1141−6545 and B2303+46. |
| J1756−2251 | 035.135 | 000.31963 | 002.75646 | 0.1805694(2) | 2.56999(6) | 1.341(7) | 1.230(7) | p, γ, s, GW | no | Confirmed. Low-mass NS companion. No geodetic precession for pulsar, indicating alignment of its spin axis with orbital angular momentum. |
| J1757−1854 | 046.518 | 000.18354 | 002.23781 | 0.6058171(3) | 2.732882(12) | 1.3406(5) | 1.3922(5) | p, γ, h3, ς GW | yes | Confirmed. Most accelerated binary, largest relative velocity, five measured PK parameters. Second-formed NS significantly more massive than first-formed NS. |
| J1759+5036 | 005.681 | 002.04298 | 006.82461 | 0.30827(12) | 2.679(12) | < 1.84 | > 0.83 | f, p | u | Confirmed. |
| J1807−2500B | 238.881 | 009.95667 | 028.92039 | 0.747033198(40) | 2.57190(73) | 1.3655(21) | 1.2064(20) | p, ς, h3 | u | Candidate. MSP - massive compact companion. System formed through exchange encounter in GC NGC 6544. Companion is either a massive WD or NS, so this could be a MSP - NS system. |
| J1811−1736 | 009.599 | 018.77917 | 034.7827 | 0.828011(9) | 2.57(10) | < 1.74 | > 0.93 | f, p | u | Confirmed. |
| J1823−3021G | 164.169 | 001.54014 | 003.00331 | 0.380466(6) | 2.65(7) | < 2.4 | > 0.44 | f,p | u | Candidate. MSP - massive compact companion. System formed through exchange encounter in GC NGC 6624. Companion is either a massive WD or NS, so this could be a MSP - NS system. |
| J1829+2456 | 024.384 | 001.17603 | 007.23684 | 0.1391435(3) | 2.60551(38) | 1.306(7) | 1.299(7) | p, s | u | Confirmed. |
| J1835−3259A | 257.147 | 009.2460 | 019.6(3) | 0.968(5) | - | [1.4] | > 0.76 | f | u | Candidate. MSP - massive compact companion. System formed through exchange encounter in GC NGC 6652. Companion is either a massive WD or NS, so this could be a MSP - NS system. |
| J1844−0128 | 034.312 | 010.60032 | 020.96779 | 0.234949(5) | - | [1.4] | > 0.74 | f, p | u | Confirmed. |
| J1846−0513 | 042.791 | 000.61302 | 004.75646 | 0.2085888(9) | 2.6287(35) | < 1.35 | > 1.28 | f, p | u | Confirmed. |
| J1901+0658 | 013.202 | 014.45477 | 032.40204 | 0.3662392(5) | 2.79(7) | < 1.68 | > 1.11 | f, p | u | Confirmed. |
| J1906+0746 | 006.941 | 000.16599 | 001.41995 | 0.0852996(6) | 2.6134(3) | 1.291(11) | 1.322(11) | p, γ, GW, G | yes | Candidate. yPSR - massive compact companion. The pulsar (only 110 kyr old) is the second-formed compact object in the system. Companion could be a recycled NS as in most other PSR - NS systems, but it could also be a massive WD, as in the cases of J1141−6545 and B2303+46. |
| J1913+1102 | 036.650 | 000.20625 | 001.75462 | 0.089531(2) | 2.8887(6) | 1.62(3) | 1.27(3) | p, γ, GW | u | Confirmed. Most massive among these systems, pulsar is most massive NS in a PSR - NS system. First known member of new population of merging, asymmetric DNSs. |
| B1913+16 | 016.940 | 000.32299 | 002.34178 | 0.6171340(4) | 2.828378(7) | 1.438(1) | 1.390(1) | p, γ, GW, h3, ς | yes | Confirmed. The Hulse-Taylor binary. First binary pulsar discovered. First NS mass measurements. Orbital decay was the first GR test in a binary pulsar, and first radiative test anywhere. This showed that gravitational waves exist. |
| J1930−1852 | 005.390 | 045.06000 | 086.89027 | 0.39886334(15) | 2.54(3) | < 1.25 | > 1.30 | f, p | u | Confirmed. Largest orbital period for this type of system. |
| J1946+2052 | 058.962 | 000.07849 | 001.15432 | 0.063848(9) | 2.50(4) | < 1.31 | > 1.18 | f, p | yes | Confirmed. Shortest orbital period for this type of system. |
| J1953+1847D | 009.933 | 010.9380 | 032.0634(1) | 0.628921(3) | 2.63(8) | < 1.4 | > 1.1 | f,p | u | PSR - NS system. Located in the GC NGC 6838 (M71). Despite the location in a GC, the system is very unlikely to have formed in an exchange encounter. Its characteristics indicate it is a Pulsar - NS system. |
| B2127+11C | 032.755 | 000.33528 | 002.51845 | 0.681395(2) | 2.71279(13) | 1.358(10) | 1.354(10) | p, γ, GW | yes | Candidate. PSR - massive compact companion. Formed through exchange encounter in GC NGC 7078 (M15), companion could be a massive WD, but generally assumed to be a NS given the large mass. Acceleration of system in the cluster precludes further improvements in precision of radiative test of GR. |
| J2140−2311B | 076.983 | 006.21565 | 019.5222(7) | 0.87938(2) | 2.53(8) | < 1.43 | > 1.11 | f,p | u | Candidate. MSP - massive compact companion. System formed through exchange encounter in GC NGC 7099 (M30). Companion is either a massive WD or NS, so this could be a MSP - NS system. |
| J2150+3427 | 001.528 | 010.59213 | 025.48802 | 0.601494(2) | 2.59(13) | < 1.67 | > 0.98 | f, p | u | Candidate. Pulsar is very slow, and was likely (mildly) recycled. If it is the second-formed object in the system, then the companion (the primary) could be a massive WD. |
| The mass constraints and the requirements for their measurement are: | |
| f: | The mass function. If only this is listed, then we indicate the minimum companion mass obtained assuming the value of the pulsar mass that appears in square brackets. If this is listed together with the rate of advance of periastron, then we can obtain a maximum estimate for the pulsar mass and a minimum estimate for the companion mass. |
| i: | Mass estimate based on measurement of deviations from Keplerian orbits caused by many-body interactions via pulsar timing. This requires a number of massive components in the system larger than 2. |
| R: | Mass ratio derived from pulsar timing. This requires a double pulsar system, only one case known (the J0737−3039 system). |
| q: | Mass ratio derived from pulsar timing and optical spectroscopy. This requires a companion WD bright enough for spectroscopic radial velocity measurements. |
| mWD: | White dwarf mass (optical). This requires a companion WD bright enough for detailed spectroscopic modeling. |
| p: | Rate of advance of periastron (timing). This requires significant orbital eccentricity. |
| γ: | Einstein delay (timing). This requires a combination of significant orbital eccentricity and compactness. |
| s: | Shape parameter of Shapiro delay (timing). All Shapiro delay parameters require the system to have a high orbital inclination and good timing precision. |
| r: | Range parameter of Shapiro delay (timing). |
| ς: | Orthometric ratio of Shapiro delay (timing) - From the Freire & Wex (2010) reparameterization of the Shapiro delay. |
| h3: | Orthometric amplitude of Shapiro delay (timing) - From the Freire & Wex (2010) reparameterization of the Shapiro delay. |
| GW: | Orbital decay (timing), caused by energy loss due to gravitational waves. Detecting this requires a compact orbit. |
| GWa: | Same as GW, but for an asymmetric system, like a pulsar-WD system. This introduces stronger constraints on alternative theories of gravity. |
| G: | Rate of geodetic precession. |
| A subscript refers to the pulsar for which we measure the parameter (this is only an issue for the J0737−3039 system). | |
| For the column on the detection of geodetic precession, the meaning of the entries is: | |
| a: | The spin of this pulsar is expected to be aligned with the orbital angular momentum of the system. This means that geodetic precession should not cause detectable changes in the pulse profile. |
| u: | The spin of this pulsar is not expected to be aligned with the orbital angular momentum of the system, but geodetic precession is too slow to cause detectable changes in the pulse profile. |
| In the following cases, the pulsar spin is not expected to be necessarily aligned with the orbital angular momentum of the system and geodetic precession should be fast enough to produce detectable changes in the pulse profile: | |
| yes: | Such changes are indeed observable, confirming the spin-orbit misalignment. |
| no: | No changes in the pulse profile are detected. This suggests the pulsar spin is aligned with the orbit after all. |
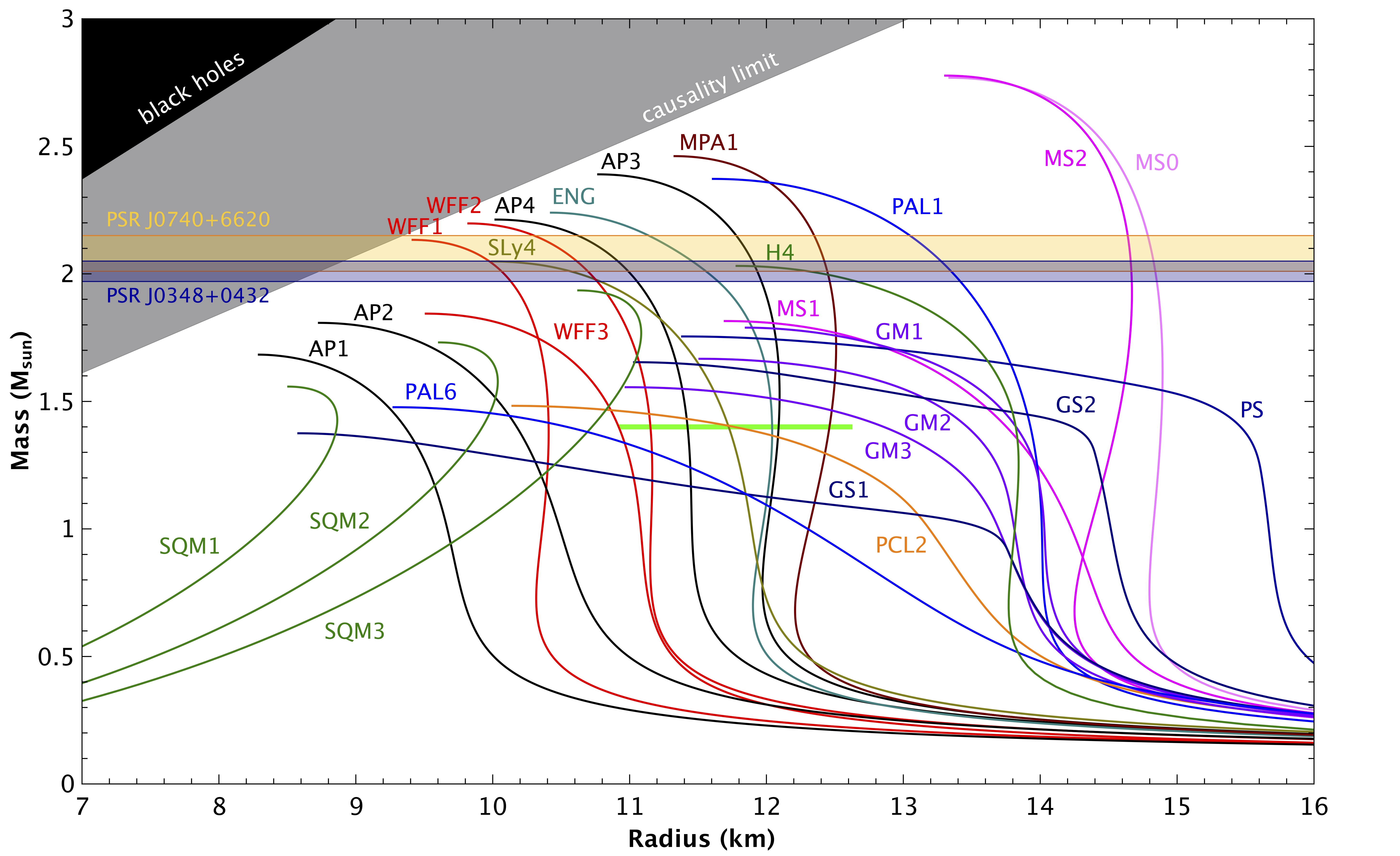
Fig. 2: Precise neutron star mass measurements are useful for a variety of
purposes. One of them is to constrain the macroscopic behaviour (in particular the
relation between density and pressure, known as the equation of state, or EOS) of the
cold, super-dense matter at the center of a neutron star. For each EOS (named in the
figure) the relation between mass and radius for all neutron stars is indicated by its
related curve. The horizontal yellow bar represents the 68.3% confidence limits for the
most massive pulsar tabulated above. If a particular EOS predicts a maximum mass smaller
than the largest measured NS mass then it is excluded.
The horizontal line segment corresponds to the 95% confidence limit range of radii for 1.4
solar mass neutron stars, this results from the multi-messenger analysis of
Koehn et al. (2025).
Figure created by Norbert Wex. Most EOSs tabulated in Lattimer & Prakash (2001)
and provided by the authors.
Latest changes to this page:
2025 Jun. 10: Added mass measurement for the PSR J1953+1847D system. Despite being located in the GC M71, the very low density of this GC implies that the M71D system is unlikely to have formed dynamically, like all other pulsar - NS candidates in GCs. Its large eccentricity, companion mass and spin period are characteristic of double neutron star systems in the Galactic disk. Very large characteristic age is consistent with formation coeval with M71. 2025 Mar. 10: Updated mass measurements for NGC 1851A. Companion is now very likely to be a massive WD. System was taken out of list of possible pulsar - NS systems.
2025 Feb. 14: Added binary mass measurement for a new PSR - WD system, PSR J1617−2258A, located in the GC M80.
2025 Jan. 15: Added mass measurements for PSR J1543−5149, a MSP - He WD system.
2024 Dec. 5:
- Added two new PSR - NS systems, PSR J0528+3529 and PSR J1844−0128,
- Added mass measurements for two new pulsar - massive WD systems, PSR J1943+2210 and PSR J2023+2853.
- Added revised mass estimate for PSR J0348+0432, which assumes orbital decay is fully relativistic. If correct, this significantly reduces the mass of PSR J0348+0432.
2024 Mar. 27:
- Added mass measurements for PSR J1748−2446ap, and binary mass measurements for PSR J1748−2446ao and PSR J1748−2446au, all located in the GC Terzan 5. The PSR J1748−2446ao system is quite massive (3.166 ± 0.024 solar masses), it could be a double neutron star system of a massive pulsar with a massive WD companion.
- Added reference on the geodetic precession of PSR J1946+2052, the recycled pulsar in the DNS with the shortest orbital period.
2024 Mar. 16: Added binary mass measurement for a new PSR - NS system, PSR J1846−0513.
2024 Feb. 14: Added mass measurements for PSR J0218+4232 and individual NS mass measurements for PSR J1518+4904.
2024 Jan. 18: Added reference on the timing of NGC 1851E. System formed through exchange encounter in GC NGC 1851. With a total mass of 3.8870 ± 0.0045 solar masses, it is by far the most massive system consisting of a pulsar and a degenerate companion that we know of. Companion is either a very massive NS or a light BH, so this could be the first pulsar - black hole system. 2023 Dec. 13: Added much improved measurements of the masses of PSR J0509+3801, a measurement of the orbital decay of this system and a much improved measurement of the binary mass of PSR J1759+5036. 2023 Dec. 6: Updated binary mass measurement for PSR B1516+02B. 2023 Nov. 23: Added mass measurement for PSR J1012−4235, a MSP - He WD system. 2023 Nov. 22: Added binary mass measurement for PSR J2150+3427, a pulsar with a massive companion where the pulsar is unusually slow.
2023 Sept. 1: Added reference on the timing solution and binary mass of PSR J1208−5936.
2023 May 25: Updated mass measurements for PSR J1757−1854.
2023 April 19: Added mass measurements for PSR J1933−6211, a MSP - CO WD system.
2023 April 14: Added mass measurements for PSR J1528−3146, a pulsar - massive WD system, and new mass estimates for PSRs J1125−6014, J1614−2230 and J1909−3744 from MeerKAT data.
2023 April 12: Added the discovery of two new pulsar - NS systems, PSRs J1155−6529 and J1208−5936, by the MMGPS survey.
2023 January 13: Added binary mass measurement for PSR J2140−2311B, an eccentric binary MSP in M30 that could potentially be a MSP - NS system.
2023 January 11: Updated mass measurements for PSR J1910−5958A from Shapiro delay (pulsar is designated as PSR J1910−5959A).
2022 December 12: Added PSR - NS system PSR J1018−1523.
2022 October 31: Added mass measurement for PSR J1125−6014, a MSP - CO WD system.
2022 March 31: Updated masses for PSR J1757−1854.
2022 March 30: Added PSR - NS system J1325−6253.
2022 March 2: Added PSR J0955−6150, an eccentric MSP - He WD system.
2021 Dec. 14: Updated mass and GR tests with the double pulsar, PSR J0737−3039A/B.
2021 July 21: Updated masses of PSR J2222−0137 and its very massive WD companion.
2021 April 5: Updated masses of the PSR J0740+6620 system.
2021 March 9: Added binary mass measurement for a new system, PSR J1823−3021G, an eccentric binary MSP in NGC 6624 that could potentially be a MSP - NS system.
2021 March 5: Added third part of the table, with list of PSR - NS systems, both confirmed (mainly by stellar evolution arguments) and candidates.
2021 Feb. 27: Added binary mass measurement for a new PSR - NS system, PSR J1759+5036.
2020 Nov. 5: Updated mass measurements for the two NSs in the PSR J1829+2456 system.
2020 Sept. 29: Updated mass measurements for PSR J1909−3744.
2020 Sept. 28: Added PSR J2045+3633, a pulsar - massive WD system.
2020 July 16: Added mass measurements for the two NSs in the PSR J1829+2456 system.
2020 July 8: Added mass measurements for the two NSs in the PSR J1913+1102 system. The system is asymmetric and demonstrates the existence of a new population of merging, asymmetric double NSs.
2020 May 8: Updated masses for the PSR J0337+1715 triple system based on the latest and most precise test of the strong equivalence principle with this system.
2020 April 9: Added updated mass measurement for the PSR J1012+5307 system and new limits on dipolar GW emission derived from these binaries.
2020 Jan. 31: Added detection of Lense-Thirring precession in the PSR J1141−6545 system.
2019 Sept. 25: Added measurement of the rate of geodetic precession for PSR J1906+0746.
2019 Sept. 16: Individual masses for both components of PSR J0514−4002A have been measured. System very likely formed via exchange encounter in the GC NGC 1851. The companion is either a massive WD or a NS.
2019 June 24: Added MSP - WD systems PSR J1949+3106 and PSR J1950+2414. The latter is an eccentric MSP - He WD system.
2019 April 16: Added MSP - WD system PSR J0740+6620, likely the most massive NS known!
2018 Sept. 14: Added eccentric MSP - He WD system PSR J2234+0611. Also, added link to the test of the universality of free fall with PSR J0337+1715.
2018 July 23: Added MSP - WD system J1748−2446am, located in GC Terzan 5.
2018 May 29: Added data for PSR J1824−2452C, from Steve Bégin's M.Sc. Thesis, University of British Columbia, 2006.
2018 May 22: Added systems with binary mass measurements (from measurement of rate of advance of periastron), where the binary mass is known to better than 10%.
2018 May 15: Added PSR - NS system J0509+3801.
2018 March 6: Replaced the ``double neutron star system'' (DNS) term by the more precise ``Pulsar - Neutron star system'' (PSR-NS), in order to avoid confusion with the LIGO/Virgo systems.
2018 March 1: Updated parameters for PSR J1713+0737, in particular the new limits on violation of gravitational symmetries.
2018 Jan. 08: Updated masses from the NANOGrav Eleven-year Data Set (PSRs J1614−2230, J1713+0737, B1855+09, J1909−3744, J1918−0642 and J2043+1711).
2017 Nov. 22: Added PSR - NS system J1757−1854.
2017 June 27: Updated mass of PSR J2222−0137.
2017 June 20: Added PSR J2053+4650.
2016 Nov. 15: Added PSR J1946+3417, and eccentric MSP - He WD system.
Imprint / Privacy policy / Back to Paulo's main page.